This is an old revision of this page, as edited by 200.120.73.176 (talk) at 00:54, 22 February 2014 (→Occurrence: no requirement for italics there). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 00:54, 22 February 2014 by 200.120.73.176 (talk) (→Occurrence: no requirement for italics there)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)
Probability density function Some log-normal density functions with identical location parameter μ but differing scale parameters σ | |||
Cumulative distribution function Cumulative distribution function of the log-normal distribution (with μ = 0 ) | |||
| Notation | |||
|---|---|---|---|
| Parameters |
σ > 0 — shape (real), μ ∈ R — log-scale | ||
| Support | x ∈ (0, +∞) | ||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy | |||
| MGF | (defined only on the negative half-axis, see text) | ||
| CF | representation is asymptotically divergent but sufficient for numerical purposes | ||
| Fisher information | |||
In probability theory, a log-normal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Likewise, if has a normal distribution, then has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values.
Log-normal is also written log normal or lognormal. The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution also has been associated with other names, such as McAlister, Gibrat and Cobb–Douglas.
A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many independent random variables each of which is positive. (This is justified by considering the central limit theorem in the log-domain.) For example, in finance, the variable could represent the compound return from a sequence of many trades (each expressed as its return + 1); or a long-term discount factor can be derived from the product of short-term discount factors. In wireless communication, the sas caused by shadowing or slow fading from random objects is often assumed to be log-normally distributed: see log-distance path loss model.
The log-normal distribution is the maximum entropy probability distribution for a random variate X for which the mean and variance of are fixed.
μ and σ
In a log-normal distribution X, the parameters denoted μ and σ are, respectively, the mean and standard deviation of the variable’s natural logarithm (by definition, the variable’s logarithm is normally distributed), which means
with Z a standard normal variable.
This relationship is true regardless of the base of the logarithmic or exponential function. If loga(Y) is normally distributed, then so is logb(Y), for any two positive numbers a, b ≠ 1. Likewise, if is log-normally distributed, then so is , where is a positive number ≠ 1.
On a logarithmic scale, μ and σ can be called the location parameter and the scale parameter, respectively.
In contrast, the mean and standard deviation of the non-logarithmized sample values are denoted m and s.d. in this article.
A log-normal distribution with mean m and variance v has parameters
Characterization
Probability density function
The probability density function of a log-normal distribution is:
This follows by applying the change-of-variables rule on the density function of a normal distribution.
Cumulative distribution function
The cumulative distribution function is
where erfc is the complementary error function, and Φ is the cumulative distribution function of the standard normal distribution.
Characteristic function and moment generating function
All moments of the log-normal distributions exist and it holds that
- .
However, the moment generating function
does not converge.
The characteristic function, E, has a number of representations. The integral itself converges for Im(t) ≤ 0. The simplest representation is obtained by Taylor expanding e and using formula for moments below, giving
This series representation is divergent for Re(σ) > 0. However, it is sufficient for evaluating the characteristic function numerically at positive as long as the upper limit in the sum above is kept bounded, n ≤ N, where
and σ < 0.1. To bring the numerical values of parameters μ, σ into the domain where strong inequality holds true one could use the fact that if X is log-normally distributed then X is also log-normally distributed with parameters μm, σm. Since , the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of φ(t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.
Another useful representation is available by means of double Taylor expansion of e.
The moment-generating function for the log-normal distribution does not exist on the domain R, but only exists on the half-interval (−∞, 0].
Properties
Location and scale
For the log-normal distribution, the location and scale properties of the distribution are more readily treated using the geometric mean and geometric standard deviation than the arithmetic mean and standard deviation.
Geometric moments
The geometric mean of the log-normal distribution is . Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.
The geometric mean (mg) can alternatively be derived from the arithmetic mean (ma) in a log-normal distribution by:
Note that the geometric mean is less than the arithmetic mean. This is due to the AM–GM inequality, and corresponds to the logarithm being convex down. The correction term can accordingly be interpreted as a convexity correction. From the point of view of stochastic calculus, this is the same correction term as in Itō's lemma for geometric Brownian motion.
The geometric standard deviation is equal to .
Arithmetic moments
If X is a lognormally distributed variable, its expected value (E – the arithmetic mean), variance (Var), and standard deviation (s.d.) are
Equivalently, parameters μ and σ can be obtained if the expected value and variance are known; it is simpler if σ is computed first:
For any real or complex number s, the s moment of log-normal X is given by
A log-normal distribution is not uniquely determined by its moments E for k ≥ 1, that is, there exists some other distribution with the same moments for all k. In fact, there is a whole family of distributions with the same moments as the log-normal distribution.
Mode and median
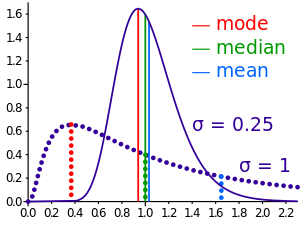
The mode is the point of global maximum of the probability density function. In particular, it solves the equation (ln ƒ)′ = 0:
The median is such a point where FX = 1/2:
Coefficient of variation
The coefficient of variation is the ratio s.d. over m (on the natural scale) and is equal to:
Partial expectation
The partial expectation of a random variable X with respect to a threshold k is defined as where is the probability density function of X. Alternatively, and using the definition of conditional expectation, it can be written as g(k)=E*P(X > k). For a log-normal random variable the partial expectation is given by:
The derivation of the formula is provided in the discussion of this Misplaced Pages entry. The partial expectation formula has applications in insurance and economics, it is used in solving the partial differential equation leading to the Black–Scholes formula.
Other
A set of data that arises from the log-normal distribution has a symmetric Lorenz curve (see also Lorenz asymmetry coefficient).
The harmonic (H), geometric (G) and arithmetic (A) means of this distribution are related; such relation is given by
Log-normal distributions are infinitely divisible.
Occurrence
The log-normal distribution is important in the description of natural phenomena. The reason is that for many natural processes of growth, growth rate is independent of size. This is also known as Gibrat's law, after Robert Gibrat (1904–1980) who formulated it for companies. It can be shown that a growth process following Gibrat's law will result in entity sizes with a log-normal distribution. Examples include:
- In biology and medicine,
- Measures of size of living tissue (length, skin area, weight);
- For highly communicable epidemics, such as SARS in 2003, if publication intervention is involved, the number of hospitalized cases is shown to satistfy the lognormal distribution with no free parameters if an entropy is assumed and the standard deviation is determined by the principle of maximum rate of entropy production.
- The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth;
- Certain physiological measurements, such as blood pressure of adult humans (after separation on male/female subpopulations)

- Consequently, reference ranges for measurements in healthy individuals are more accurately estimated by assuming a log-normal distribution than by assuming a symmetric distribution about the mean.
- In colloidal chemistry,
- Particle size distributions
- In hydrology, the log-normal distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.
- The image on the right illustrates an example of fitting the log-normal distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of a cumulative frequency analysis.
- in social sciences and demographics
- In economics, there is evidence that the income of 97%–99% of the population is distributed log-normally.
- In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal (these variables behave like compound interest, not like simple interest, and so are multiplicative). However, some mathematicians such as Benoît Mandelbrot have argued that log-Lévy distributions which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. Indeed stock price distributions typically exhibit a fat tail.
- city sizes
- technology
- In reliability analysis, the lognormal distribution is often used to model times to repair a maintainable system.
- In wireless communication, "the local-mean power expressed in logarithmic values, such as dB or neper, has a normal (i.e., Gaussian) distribution."
- It has been proposed that coefficients of friction and wear may be treated as having a lognormal distribution
- In spray process, such as droplet impact, the size of secondary produced droplet has a lognormal distribution, with the standard deviation : determined by the principle of maximum rate of entropy production If the lognormal distribution is inserted into the Shannon entropy expression and if the rate of entropy production is maximized (principle of maximum rate of entropy production), then σ is given by : and with this parameter the droplet size distribution for spray process is well predicted. It is an open question whether this value of σ has some generality for other cases, though for spreading of communicable epidemics, σ is shown also to take this value.
Maximum likelihood estimation of parameters
For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that
where by ƒL we denote the probability density function of the log-normal distribution and by ƒN that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:
Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, ℓL and ℓN, reach their maximum with the same μ and σ. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that
Multivariate log-normal
If is a multivariate normal distribution then has a multivariate log-normal distribution with mean
Generating log-normally distributed random variates
Given a random variate Z drawn from the normal distribution with 0 mean and 1 standard deviation, then the variate
has a log-normal distribution with parameters and .
Related distributions
- If is a normal distribution, then
- If is distributed log-normally, then is a normal random variable.
- If are n independent log-normally distributed variables, and , then Y is also distributed log-normally:
- Let be independent log-normally distributed variables with possibly varying σ and μ parameters, and . The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 has been characterized and it does not resemble any log-normal distribution. A commonly used approximation (due to L.F. Fenton, but previously stated by R.I. Wilkinson without mathematical justification) is obtained by matching the mean and variance:
In the case that all have the same variance parameter , these formulas simplify to
- If , then X + c is said to have a shifted log-normal distribution with support x ∈ (c, +∞). E = E + c, Var = Var.
- If , then
- If , then
- If then for
- Lognormal distribution is a special case of semi-bounded Johnson distribution
- If with , then (Suzuki distribution)
Similar distributions
A substitute for the log-normal whose integral can be expressed in terms of more elementary functions can be obtained based on the logistic distribution to get an approximation for the CDF
This is a log-logistic distribution.
See also
Notes
- ^ Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-58495-7, MR 1299979
- Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics. Elsevier: 219–230. Retrieved 2011-06-02.
- "Lognormal mean and variance"
- Leipnik, Roy B. (1991), "On Lognormal Random Variables: I – The Characteristic Function", Journal of the Australian Mathematical Society Series B, 32, 327–347.
- ^ Daniel Dufresne (2009), SUMS OF LOGNORMALS, Centre for Actuarial Studies, University of Melbourne.
- Leslie E. Daly, Geoffrey Joseph Bourke (2000) Interpretation and uses of medical statistics Edition: 5. Wiley-Blackwell ISBN 0-632-04763-1, ISBN 978-0-632-04763-5 (page 89)
- Damgaard, Christian; Weiner, Jacob (2000). "Describing inequality in plant size or fecundity". Ecology. 81 (4): 1139–1142. doi:10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
- Rossman LA (1990) "Design stream flows based on harmonic means". J Hydraulic Engineering ASCE 116 (7) 946–950
- Sutton, J. (1997), "Gibrat's Legacy", Journal of Economic Literature XXXV, 40–59.
- Huxley, Julian S. (1932). Problems of relative growth. London. ISBN 0-486-61114-0. OCLC 476909537.
{{cite book}}: Invalid|ref=harv(help) - ^ WB, Wang (2013). "Modelling the spreading rate of controlled communicable epidemics through an entropy-based thermodynamic model". SCIENCE CHINA Physics, Mechanics & Astronomy. pp. 2143–2150.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Makuch, Robert W. (1979). "Justification for the lognormal distribution as a model for blood pressure". Journal of Chronic Diseases. 32 (3): 245–250. doi:10.1016/0021-9681(79)90070-5. Retrieved 27 February 2012.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Ritzema (ed.), H.P. (1994). Frequency and Regression Analysis (PDF). Chapter 6 in: Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. pp. 175–224. ISBN 90-70754-33-9.
{{cite book}}:|last=has generic name (help) - Clementi, Fabio; Gallegati, Mauro (2005) "Pareto's law of income distribution: Evidence for Germany, the United Kingdom, and the United States", EconWPA
- Black, Fischer and Myron Scholes, "The Pricing of Options and Corporate Liabilities", Journal of Political Economy, Vol. 81, No. 3, (May/June 1973), pp. 637–654.
- Madelbrot, Beniot (2004). The (mis-)Behaviour of Markets.
- Bunchen, P., Advanced Option Pricing, University of Sydney coursebook, 2007
- O'Connor, Patrick; Kleyner, Andre (2011). Practical Reliability Engineering. John Wiley & Sons. p. 35. ISBN 978-0-470-97982-2.
- http://wireless.per.nl/reference/chaptr03/shadow/shadow.htm
- Attention: This template ({{cite doi}}) is deprecated. To cite the publication identified by doi:10.1016/j.ress.2007.09.005, please use {{cite journal}} (if it was published in a bona fide academic journal, otherwise {{cite report}} with
|doi=10.1016/j.ress.2007.09.005instead. - ^ Wu, Zi-Niu (July 2003). "Prediction of the size distribution of secondary ejected droplets by crown splashing of droplets impinging on a solid wall". Probabilistic Engineering Mechanics. 18 (3): 241–249. doi:doi.org/10.1016/S0266-8920(03)00028-6.
{{cite journal}}: Check|doi=value (help) Cite error: The named reference "wu" was defined multiple times with different content (see the help page). - Tarmast, Ghasem (2001) "Multivariate Log–Normal Distribution" ISI Proceedings: Seoul 53rd Session 2001
- Gao, X.; Xu, H; Ye, D. (2009), "Asymptotic Behaviors of Tail Density for Sum of Correlated Lognormal Variables". International Journal of Mathematics and Mathematical Sciences, vol. 2009, Article ID 630857. doi:10.1155/2009/630857
- Template:Cite DOI
References
- Aitchison, J. and Brown, J.A.C. (1957) The Lognormal Distribution, Cambridge University Press.
- E. Limpert, W. Stahel and M. Abbt (2001) Log-normal Distributions across the Sciences: Keys and Clues, BioScience, 51 (5), 341–352.
- Eric W. Weisstein et al. Log Normal Distribution at MathWorld. Electronic document, retrieved October 26, 2006.
Further reading
- Robert Brooks, Jon Corson, and J. Donal Wales. "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion", in Advances in Futures and Options Research, volume 7, 1994.
External links
Template:Common univariate probability distributions
Categories:









 is asymptotically divergent but sufficient for numerical purposes
is asymptotically divergent but sufficient for numerical purposes
 is log-normally distributed, then
is log-normally distributed, then  has a normal distribution. Likewise, if
has a normal distribution. Likewise, if  has a normal distribution, then
has a normal distribution, then  has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values.
has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values.
 are fixed.
are fixed.

 is log-normally distributed, then so is
is log-normally distributed, then so is  , where
, where  is a positive number ≠ 1.
is a positive number ≠ 1.



 .
.

 as long as the upper limit in the sum above is kept bounded, n ≤ N, where
as long as the upper limit in the sum above is kept bounded, n ≤ N, where

 , the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of φ(t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.
, the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of φ(t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.
 . Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.
. Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.

 can accordingly be interpreted as a
can accordingly be interpreted as a  .
.






 where
where  is the probability density function of X. Alternatively, and using the definition of
is the probability density function of X. Alternatively, and using the definition of 

 determined by the principle of maximum rate of entropy production If the lognormal distribution is inserted into the Shannon entropy expression and if the rate of entropy production is maximized (principle of maximum rate of entropy production), then σ is given by :
determined by the principle of maximum rate of entropy production If the lognormal distribution is inserted into the Shannon entropy expression and if the rate of entropy production is maximized (principle of maximum rate of entropy production), then σ is given by : and with this parameter the droplet size distribution for spray process is well predicted. It is an open question whether this value of σ has some generality for other cases, though for spreading of communicable epidemics, σ is shown also to take this value.
and with this parameter the droplet size distribution for spray process is well predicted. It is an open question whether this value of σ has some generality for other cases, though for spreading of communicable epidemics, σ is shown also to take this value.


 is a
is a  has a multivariate log-normal distribution with mean
has a multivariate log-normal distribution with mean



 and
and  is a
is a 
 is distributed log-normally, then
is distributed log-normally, then  is a normal random variable.
is a normal random variable. are n
are n  , then Y is also distributed log-normally:
, then Y is also distributed log-normally:
 be independent log-normally distributed variables with possibly varying σ and μ parameters, and
be independent log-normally distributed variables with possibly varying σ and μ parameters, and  . The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 has been characterized and it does not resemble any log-normal distribution. A commonly used approximation (due to L.F. Fenton, but previously stated by R.I. Wilkinson without mathematical justification) is obtained by matching the mean and variance:
. The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 has been characterized and it does not resemble any log-normal distribution. A commonly used approximation (due to L.F. Fenton, but previously stated by R.I. Wilkinson without mathematical justification) is obtained by matching the mean and variance:
 have the same variance parameter
have the same variance parameter  , these formulas simplify to
, these formulas simplify to



 for
for 
 with
with  , then
, then  (
(