Misplaced Pages

q-Weibull distribution

Probability density function
Cumulative distribution function
Parameters	${\displaystyle q<2}$ shape (real) ${\displaystyle \lambda >0}$ rate (real) ${\displaystyle \kappa >0\,}$ shape (real)
Support	${\displaystyle x\in [0;+\infty )\!{\text{ for }}q\geq 1}$ ${\displaystyle x\in [0;{\lambda \over {(1-q)^{1/\kappa }}}){\text{ for }}q<1}$
PDF	${\displaystyle {\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}^{-(x/\lambda )^{\kappa }}&x\geq 0\\0&x<0\end{cases}}}$
CDF	${\displaystyle {\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}}$
Mean	(see article)

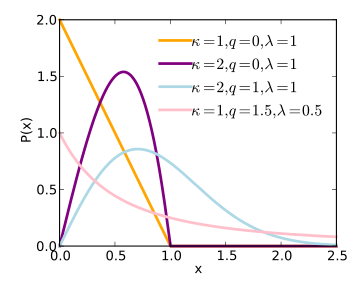
In statistics, the q-Weibull distribution is a probability distribution that generalizes the Weibull distribution and the Lomax distribution (Pareto Type II). It is one example of a Tsallis distribution.

Characterization

Probability density function

The probability density function of a q-Weibull random variable is:

${\displaystyle f(x;q,\lambda ,\kappa )={\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}(-(x/\lambda )^{\kappa })&x\geq 0,\\0&x<0,\end{cases}}}$

where q < 2, ${\displaystyle \kappa }$ > 0 are shape parameters and λ > 0 is the scale parameter of the distribution and

${\displaystyle e_{q}(x)={\begin{cases}\exp(x)&{\text{if }}q=1,\\^{1/(1-q)}&{\text{if }}q\neq 1{\text{ and }}1+(1-q)x>0,\\0^{1/(1-q)}&{\text{if }}q\neq 1{\text{ and }}1+(1-q)x\leq 0,\\\end{cases}}}$

is the q-exponential

Cumulative distribution function

The cumulative distribution function of a q-Weibull random variable is:

${\displaystyle {\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}}$

where

${\displaystyle \lambda '={\lambda \over (2-q)^{1 \over \kappa }}}$

${\displaystyle q'={1 \over (2-q)}}$

Mean

The mean of the q-Weibull distribution is

${\displaystyle \mu (q,\kappa ,\lambda )={\begin{cases}\lambda \,\left(2+{\frac {1}{1-q}}+{\frac {1}{\kappa }}\right)(1-q)^{-{\frac {1}{\kappa }}}\,B\left&q<1\\\lambda \,\Gamma (1+{\frac {1}{\kappa }})&q=1\\\lambda \,(2-q)(q-1)^{-{\frac {1+\kappa }{\kappa }}}\,B\left&1<q<1+{\frac {1+2\kappa }{1+\kappa }}\\\infty &1+{\frac {\kappa }{\kappa +1}}\leq q<2\end{cases}}}$

where ${\displaystyle B()}$ is the Beta function and ${\displaystyle \Gamma ()}$ is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.

Relationship to other distributions

The q-Weibull is equivalent to the Weibull distribution when q = 1 and equivalent to the q-exponential when ${\displaystyle \kappa =1}$

The q-Weibull is a generalization of the Weibull, as it extends this distribution to the cases of finite support (q < 1) and to include heavy-tailed distributions ${\displaystyle (q\geq 1+{\frac {\kappa }{\kappa +1}})}$.

The q-Weibull is a generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support and adds the ${\displaystyle \kappa }$ parameter. The Lomax parameters are:

${\displaystyle \alpha ={{2-q} \over {q-1}}~,~\lambda _{\text{Lomax}}={1 \over {\lambda (q-1)}}}$

As the Lomax distribution is a shifted version of the Pareto distribution, the q-Weibull for ${\displaystyle \kappa =1}$ is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:

${\displaystyle {\text{If }}X\sim \operatorname {{\mathit {q}}-Weibull} (q,\lambda ,\kappa =1){\text{ and }}Y\sim \left,{\text{ then }}X\sim Y\,}$

See also

• Constantino Tsallis
• Tsallis statistics
• Tsallis entropy
• Tsallis distribution
• q-Gaussian

References

1. ^ Picoli, S. Jr.; Mendes, R. S.; Malacarne, L. C. (2003). "q-exponential, Weibull, and q-Weibull distributions: an empirical analysis". Physica A: Statistical Mechanics and Its Applications. 324 (3): 678–688. arXiv:cond-mat/0301552. Bibcode:2003PhyA..324..678P. doi:10.1016/S0378-4371(03)00071-2. S2CID 119361445.
2. Naudts, Jan (2010). "The q-exponential family in statistical physics". Journal of Physics: Conference Series. 201 (1): 012003. arXiv:0911.5392. Bibcode:2010JPhCS.201a2003N. doi:10.1088/1742-6596/201/1/012003. S2CID 119276469.
3. Umarov, Sabir; Tsallis, Constantino; Steinberg, Stanly (2008). "On a q-Central Limit Theorem Consistent with Nonextensive Statistical Mechanics" (PDF). Milan Journal of Mathematics. 76: 307–328. doi:10.1007/s00032-008-0087-y. S2CID 55967725. Retrieved 9 June 2014.

• Statistical mechanics
• Continuous distributions
• Probability distributions with non-finite variance