Probability density function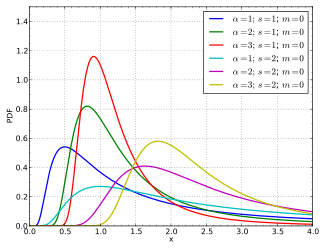 | |||
Cumulative distribution function | |||
| Parameters |
shape. (Optionally, two more parameters) scale (default: ) location of minimum (default: ) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy | , where is the Euler–Mascheroni constant. | ||
| MGF | Note: Moment exists if | ||
| CF | |||
The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function
where α > 0 is a shape parameter. It can be generalised to include a location parameter m (the minimum) and a scale parameter s > 0 with the cumulative distribution function
Named for Maurice Fréchet who wrote a related paper in 1927, further work was done by Fisher and Tippett in 1928 and by Gumbel in 1958.
Characteristics
The single parameter Fréchet, with parameter has standardized moment
(with ) defined only for
where is the Gamma function.
In particular:
- For the expectation is
- For the variance is
The quantile of order can be expressed through the inverse of the distribution,
- .
In particular the median is:
The mode of the distribution is
Especially for the 3-parameter Fréchet, the first quartile is and the third quartile
Also the quantiles for the mean and mode are:
Applications

- In hydrology, the Fréchet distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges. The blue picture, made with CumFreq, illustrates an example of fitting the Fréchet distribution to ranked annually maximum one-day rainfalls in Oman showing also the 90% confidence belt based on the binomial distribution. The cumulative frequencies of the rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
However, in most hydrological applications, the distribution fitting is via the generalized extreme value distribution as this avoids imposing the assumption that the distribution does not have a lower bound (as required by the Frechet distribution).

- In decline curve analysis, a declining pattern the time series data of oil or gas production rate over time for a well can be described by the Fréchet distribution.
- One test to assess whether a multivariate distribution is asymptotically dependent or independent consists of transforming the data into standard Fréchet margins using the transformation and then mapping from Cartesian to pseudo-polar coordinates . Values of correspond to the extreme data for which at least one component is large while approximately 1 or 0 corresponds to only one component being extreme.
- In Economics it is used to model the idiosyncratic component of preferences of individuals for different products (Industrial Organization), locations (Urban Economics), or firms (Labor Economics).
Related distributions
- The cumulative distribution function of the Frechet distribution solves the maximum stability postulate equation
- Scaling relations
- If (continuous uniform distribution) then
- If then its reciprocal is Weibull-distributed:
- If then
- If and then
Properties
- The Frechet distribution is a max stable distribution
- The negative of a random variable having a Frechet distribution is a min stable distribution
See also
| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2011) (Learn how and when to remove this message) |
References
- ^ Muraleedharan, G.; Guedes Soares, C.; Lucas, Cláudia (2011). "Characteristic and moment generating functions of generalised extreme value distribution (GEV)". In Wright, Linda L. (ed.). Sea Level Rise, Coastal Engineering, Shorelines, and Tides. Nova Science Publishers. Chapter 14, pp. 269–276. ISBN 978-1-61728-655-1.
- Khan, M.S.; Pasha, G.R.; Pasha, A.H. (February 2008). "Theoretical analysis of inverse Weibull distribution" (PDF). WSEAS Transactions on Mathematics. 7 (2): 30–38.
- de Gusmão, Felipe R.S.; Ortega, Edwin M.M.; Cordeiro, Gauss M. (2011). "The generalized inverse Weibull distribution". Statistical Papers. 52 (3). Springer-Verlag: 591–619. doi:10.1007/s00362-009-0271-3. ISSN 0932-5026.
- Fréchet, M. (1927). "Sur la loi de probabilité de l'écart maximum" [On the probability distribution of the maximum deviation]. Annales Polonici Mathematici (in French). 6: 93.
- Fisher, R.A.; Tippett, L.H.C. (1928). "Limiting forms of the frequency distribution of the largest and smallest member of a sample". Proceedings of the Cambridge Philosophical Society. 24 (2): 180–190. Bibcode:1928PCPS...24..180F. doi:10.1017/S0305004100015681. S2CID 123125823.
- Gumbel, E.J. (1958). Statistics of Extremes. New York, NY: Columbia University Press. OCLC 180577.
- Coles, Stuart (2001). An Introduction to Statistical Modeling of Extreme Values. Springer-Verlag. ISBN 978-1-85233-459-8.
- Lee, Se Yoon; Mallick, Bani (2021). "Bayesian Hierarchical Modeling: Application Towards Production Results in the Eagle Ford Shale of South Texas". Sankhya B. 84: 1–43. doi:10.1007/s13571-020-00245-8.
Further reading
- Kotz, S.; Nadarajah, S. (2000). Extreme Value Distributions: Theory and applications. World Scientific. ISBN 1-86094-224-5.
External links
- Hurairah, Ahmed; Ibrahim, Noor Akma; bin Daud, Isa; Haron, Kassim (February 2005). "An application of a new extreme value distribution to air pollution data". Management of Environmental Quality. 16 (1): 17–25. doi:10.1108/14777830510574317. ISSN 1477-7835.
- "wfrechstat: Mean and variance for the Frechet distribution". Wave Analysis for Fatigue and Oceanography (WAFO) (Matlab software & docs). Centre for Mathematical Science. Lund University / Lund Institute of Technology. Retrieved 11 November 2023 – via www.maths.lth.se.


 )
) 
 )
)









 , where
, where  is the
is the  exists if
exists if 


 has
has 
 ) defined only for
) defined only for 

 is the
is the  the
the 
 the
the 
 of order
of order  can be expressed through the inverse of the distribution,
can be expressed through the inverse of the distribution,
 .
.

 and the third quartile
and the third quartile



 and then mapping from Cartesian to pseudo-polar coordinates
and then mapping from Cartesian to pseudo-polar coordinates  . Values of
. Values of  correspond to the extreme data for which at least one component is large while
correspond to the extreme data for which at least one component is large while  approximately 1 or 0 corresponds to only one component being extreme.
approximately 1 or 0 corresponds to only one component being extreme. (
(
 then its reciprocal is
then its reciprocal is 
 then
then 
 and
and  then
then 