Misplaced Pages

Kaniadakis logistic distribution

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Kaniadakis Logistic distribution) Probability distribution
The topic of this article may not meet Misplaced Pages's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.
Find sources: "Kaniadakis logistic distribution" – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message)
This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.
Find sources: "Kaniadakis logistic distribution" – news · newspapers · books · scholar · JSTOR (July 2022)
κ-Logistic distribution
Probability density function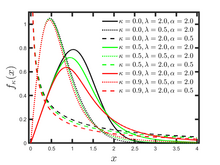Plot of the κ-Logistic distribution for typical κ-values and β = 1 {\displaystyle \beta =1} . The case κ = 0 {\displaystyle \kappa =0} corresponds to the ordinary Logistic distribution.
Cumulative distribution functionPlots of the cumulative κ-Logistic distribution for typical κ-values and β = 1 {\displaystyle \beta =1} . The case κ = 0 {\displaystyle \kappa =0} corresponds to the ordinary Logistic case.
Parameters 0 ≤ κ < 1 {\displaystyle 0\leq \kappa <1}
α > 0 {\displaystyle \alpha >0} shape (real)
β > 0 {\displaystyle \beta >0} rate (real)
λ > 0 {\displaystyle \lambda >0}
Support x ∈ [ 0 , ∞ ) {\displaystyle x\in [0,\infty )}
PDF λ α β x α − 1 1 + κ 2 β 2 x 2 α exp κ ⁡ ( − β x α ) [ 1 + ( λ − 1 ) exp κ ⁡ ( − β x α ) ] 2 {\displaystyle {\frac {\lambda \alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}{\frac {\exp _{\kappa }(-\beta x^{\alpha })}{^{2}}}}
CDF 1 − exp κ ⁡ ( − β x α ) 1 + ( λ − 1 ) exp κ ⁡ ( − β x α ) {\displaystyle {\frac {1-\exp _{\kappa }(-\beta x^{\alpha })}{1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })}}}

The Kaniadakis Logistic distribution (also known as κ-Logisticdistribution) is a generalized version of the Logistic distribution associated with the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Logistic probability distribution describes the population kinetics behavior of bosonic ( 0 < λ < 1 {\displaystyle 0<\lambda <1} ) or fermionic ( λ > 1 {\displaystyle \lambda >1} ) character.

Definitions

Probability density function

The Kaniadakis κ-Logistic distribution is a four-parameter family of continuous statistical distributions, which is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics. This distribution has the following probability density function:

f κ ( x ) = λ α β x α − 1 1 + κ 2 β 2 x 2 α exp κ ⁡ ( − β x α ) [ 1 + ( λ − 1 ) exp κ ⁡ ( − β x α ) ] 2 {\displaystyle f_{_{\kappa }}(x)={\frac {\lambda \alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}{\frac {\exp _{\kappa }(-\beta x^{\alpha })}{^{2}}}}

valid for x ≥ 0 {\displaystyle x\geq 0} , where 0 ≤ | κ | < 1 {\displaystyle 0\leq |\kappa |<1} is the entropic index associated with the Kaniadakis entropy, β > 0 {\displaystyle \beta >0} is the rate parameter, λ > 0 {\displaystyle \lambda >0} , and α > 0 {\displaystyle \alpha >0} is the shape parameter.

The Logistic distribution is recovered as κ → 0. {\displaystyle \kappa \rightarrow 0.}

Cumulative distribution function

The cumulative distribution function of κ-Logistic is given by

F κ ( x ) = 1 − exp κ ⁡ ( − β x α ) 1 + ( λ − 1 ) exp κ ⁡ ( − β x α ) {\displaystyle F_{\kappa }(x)={\frac {1-\exp _{\kappa }(-\beta x^{\alpha })}{1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })}}}

valid for x ≥ 0 {\displaystyle x\geq 0} . The cumulative Logistic distribution is recovered in the classical limit κ → 0 {\displaystyle \kappa \rightarrow 0} .

Survival and hazard functions

The survival distribution function of κ-Logistic distribution is given by

S κ ( x ) = λ exp κ ⁡ ( β x α ) + λ − 1 {\displaystyle S_{\kappa }(x)={\frac {\lambda }{\exp _{\kappa }(\beta x^{\alpha })+\lambda -1}}}

valid for x ≥ 0 {\displaystyle x\geq 0} . The survival Logistic distribution is recovered in the classical limit κ → 0 {\displaystyle \kappa \rightarrow 0} .

The hazard function associated with the κ-Logistic distribution is obtained by the solution of the following evolution equation:

S κ ( x ) d x = − h κ S κ ( x ) ( 1 − λ − 1 λ S κ ( x ) ) {\displaystyle {\frac {S_{\kappa }(x)}{dx}}=-h_{\kappa }S_{\kappa }(x)\left(1-{\frac {\lambda -1}{\lambda }}S_{\kappa }(x)\right)}

with S κ ( 0 ) = 1 {\displaystyle S_{\kappa }(0)=1} , where h κ {\displaystyle h_{\kappa }} is the hazard function:

h κ = α β x α − 1 1 + κ 2 β 2 x 2 α {\displaystyle h_{\kappa }={\frac {\alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}}

The cumulative Kaniadakis κ-Logistic distribution is related to the hazard function by the following expression:

S κ = e − H κ ( x ) {\displaystyle S_{\kappa }=e^{-H_{\kappa }(x)}}

where H κ ( x ) = ∫ 0 x h κ ( z ) d z {\displaystyle H_{\kappa }(x)=\int _{0}^{x}h_{\kappa }(z)dz} is the cumulative hazard function. The cumulative hazard function of the Logistic distribution is recovered in the classical limit κ → 0 {\displaystyle \kappa \rightarrow 0} .

Related distributions

  • The survival function of the κ-Logistic distribution represents the κ-deformation of the Fermi-Dirac function, and becomes a Fermi-Dirac distribution in the classical limit κ → 0 {\displaystyle \kappa \rightarrow 0} .
  • The κ-Logistic distribution is a generalization of the κ-Weibull distribution when λ = 1 {\displaystyle \lambda =1} .
  • A κ-Logistic distribution corresponds to a Half-Logistic distribution when λ = 2 {\displaystyle \lambda =2} , α = 1 {\displaystyle \alpha =1} and κ = 0 {\displaystyle \kappa =0} .
  • The ordinary Logistic distribution is a particular case of a κ-Logistic distribution, when κ = 0 {\displaystyle \kappa =0} .

Applications

The κ-Logistic distribution has been applied in several areas, such as:

  • In quantum statistics, the survival function of the κ-Logistic distribution represents the most general expression of the Fermi-Dirac function, reducing to the Fermi-Dirac distribution in the limit κ → 0 {\displaystyle \kappa \rightarrow 0} .

See also

References

  1. ^ Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.
  2. Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. (2011). "Kaniadakis statistics and the quantum H-theorem". Physics Letters A. 375 (3): 352–355. Bibcode:2011PhLA..375..352S. doi:10.1016/j.physleta.2010.11.045.
  3. Kaniadakis, G. (2001). "H-theorem and generalized entropies within the framework of nonlinear kinetics". Physics Letters A. 288 (5–6): 283–291. arXiv:cond-mat/0109192. Bibcode:2001PhLA..288..283K. doi:10.1016/S0375-9601(01)00543-6. S2CID 119445915.
  4. Lourek, Imene; Tribeche, Mouloud (2017). "Thermodynamic properties of the blackbody radiation: A Kaniadakis approach". Physics Letters A. 381 (5): 452–456. Bibcode:2017PhLA..381..452L. doi:10.1016/j.physleta.2016.12.019.

External links

Categories:
Kaniadakis logistic distribution Add topic