Technique of integral evaluation
In mathematics , a trigonometric substitution replaces a trigonometric function for another expression. In calculus , trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.
Case I: Integrands containing a − x
Let
x
=
a
sin
θ
,
{\displaystyle x=a\sin \theta ,}
identity
1
−
sin
2
θ
=
cos
2
θ
.
{\displaystyle 1-\sin ^{2}\theta =\cos ^{2}\theta .}
Examples of Case I
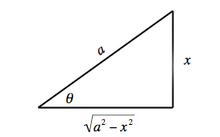
Geometric construction for Case I Example 1
In the integral
∫
d
x
a
2
−
x
2
,
{\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},}
we may use
x
=
a
sin
θ
,
d
x
=
a
cos
θ
d
θ
,
θ
=
arcsin
x
a
.
{\displaystyle x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.}
Then,
∫
d
x
a
2
−
x
2
=
∫
a
cos
θ
d
θ
a
2
−
a
2
sin
2
θ
=
∫
a
cos
θ
d
θ
a
2
(
1
−
sin
2
θ
)
=
∫
a
cos
θ
d
θ
a
2
cos
2
θ
=
∫
d
θ
=
θ
+
C
=
arcsin
x
a
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\&=\int d\theta \\&=\theta +C\\&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}
The above step requires that
a
>
0
{\displaystyle a>0}
cos
θ
>
0.
{\displaystyle \cos \theta >0.}
a
{\displaystyle a}
a
2
,
{\displaystyle a^{2},}
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
For a definite integral, one must figure out how the bounds of integration change. For example, as
x
{\displaystyle x}
0
{\displaystyle 0}
a
/
2
,
{\displaystyle a/2,}
sin
θ
{\displaystyle \sin \theta }
0
{\displaystyle 0}
1
/
2
,
{\displaystyle 1/2,}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6.
{\displaystyle \pi /6.}
∫
0
a
/
2
d
x
a
2
−
x
2
=
∫
0
π
/
6
d
θ
=
π
6
.
{\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.}
Some care is needed when picking the bounds. Because integration above requires that
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6.
{\displaystyle \pi /6.}
θ
{\displaystyle \theta }
π
{\displaystyle \pi }
5
π
/
6
,
{\displaystyle 5\pi /6,}
Alternatively, fully evaluate the indefinite integrals before applying the boundary conditions. In that case, the antiderivative gives
∫
0
a
/
2
d
x
a
2
−
x
2
=
arcsin
(
x
a
)
|
0
a
/
2
=
arcsin
(
1
2
)
−
arcsin
(
0
)
=
π
6
{\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}}
Example 2
The integral
∫
a
2
−
x
2
d
x
,
{\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx,}
may be evaluated by letting
x
=
a
sin
θ
,
d
x
=
a
cos
θ
d
θ
,
θ
=
arcsin
x
a
,
{\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\dfrac {x}{a}},}
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\textstyle {\sqrt {a^{2}}}=a,}
−
π
/
2
≤
θ
≤
π
/
2
{\textstyle -\pi /2\leq \theta \leq \pi /2}
cos
θ
≥
0
{\displaystyle \cos \theta \geq 0}
cos
2
θ
=
cos
θ
.
{\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .}
Then,
∫
a
2
−
x
2
d
x
=
∫
a
2
−
a
2
sin
2
θ
(
a
cos
θ
)
d
θ
=
∫
a
2
(
1
−
sin
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
a
2
(
cos
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
(
a
cos
θ
)
(
a
cos
θ
)
d
θ
=
a
2
∫
cos
2
θ
d
θ
=
a
2
∫
(
1
+
cos
2
θ
2
)
d
θ
=
a
2
2
(
θ
+
1
2
sin
2
θ
)
+
C
=
a
2
2
(
θ
+
sin
θ
cos
θ
)
+
C
=
a
2
2
(
arcsin
x
a
+
x
a
1
−
x
2
a
2
)
+
C
=
a
2
2
arcsin
x
a
+
x
2
a
2
−
x
2
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\&=a^{2}\int \cos ^{2}\theta \,d\theta \\&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}
For a definite integral, the bounds change once the substitution is performed and are determined using the equation
θ
=
arcsin
x
a
,
{\textstyle \theta =\arcsin {\dfrac {x}{a}},}
−
π
/
2
≤
θ
≤
π
/
2.
{\textstyle -\pi /2\leq \theta \leq \pi /2.}
For example, the definite integral
∫
−
1
1
4
−
x
2
d
x
,
{\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,}
may be evaluated by substituting
x
=
2
sin
θ
,
d
x
=
2
cos
θ
d
θ
,
{\displaystyle x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,}
θ
=
arcsin
x
2
.
{\textstyle \theta =\arcsin {\dfrac {x}{2}}.}
Because
arcsin
(
1
/
2
)
=
π
/
6
{\displaystyle \arcsin(1/{2})=\pi /6}
arcsin
(
−
1
/
2
)
=
−
π
/
6
,
{\displaystyle \arcsin(-1/2)=-\pi /6,}
∫
−
1
1
4
−
x
2
d
x
=
∫
−
π
/
6
π
/
6
4
−
4
sin
2
θ
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
1
−
sin
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
cos
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
(
2
cos
θ
)
(
2
cos
θ
)
d
θ
=
4
∫
−
π
/
6
π
/
6
cos
2
θ
d
θ
=
4
∫
−
π
/
6
π
/
6
(
1
+
cos
2
θ
2
)
d
θ
=
2
[
θ
+
1
2
sin
2
θ
]
−
π
/
6
π
/
6
=
[
2
θ
+
sin
2
θ
]
|
−
π
/
6
π
/
6
=
(
π
3
+
sin
π
3
)
−
(
−
π
3
+
sin
(
−
π
3
)
)
=
2
π
3
+
3
.
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&=2\left_{-\pi /6}^{\pi /6}={\Biggl |}_{-\pi /6}^{\pi /6}\\&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}
On the other hand, direct application of the boundary terms to the previously obtained formula for the antiderivative yields
∫
−
1
1
4
−
x
2
d
x
=
[
2
2
2
arcsin
x
2
+
x
2
2
2
−
x
2
]
−
1
1
=
(
2
arcsin
1
2
+
1
2
4
−
1
)
−
(
2
arcsin
(
−
1
2
)
+
−
1
2
4
−
1
)
=
(
2
⋅
π
6
+
3
2
)
−
(
2
⋅
(
−
π
6
)
−
3
2
)
=
2
π
3
+
3
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left_{-1}^{1}\\&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}
Case II: Integrands containing a + x
Let
x
=
a
tan
θ
,
{\displaystyle x=a\tan \theta ,}
1
+
tan
2
θ
=
sec
2
θ
.
{\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta .}
Examples of Case II
Geometric construction for Case II Example 1
In the integral
∫
d
x
a
2
+
x
2
{\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}}
we may write
x
=
a
tan
θ
,
d
x
=
a
sec
2
θ
d
θ
,
θ
=
arctan
x
a
,
{\displaystyle x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},}
so that the integral becomes
∫
d
x
a
2
+
x
2
=
∫
a
sec
2
θ
d
θ
a
2
+
a
2
tan
2
θ
=
∫
a
sec
2
θ
d
θ
a
2
(
1
+
tan
2
θ
)
=
∫
a
sec
2
θ
d
θ
a
2
sec
2
θ
=
∫
d
θ
a
=
θ
a
+
C
=
1
a
arctan
x
a
+
C
,
{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\&=\int {\frac {d\theta }{a}}\\&={\frac {\theta }{a}}+C\\&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}}
provided
a
≠
0.
{\displaystyle a\neq 0.}
For a definite integral, the bounds change once the substitution is performed and are determined using the equation
θ
=
arctan
x
a
,
{\displaystyle \theta =\arctan {\frac {x}{a}},}
−
π
2
<
θ
<
π
2
.
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.}
For example, the definite integral
∫
0
1
4
d
x
1
+
x
2
{\displaystyle \int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,}
may be evaluated by substituting
x
=
tan
θ
,
d
x
=
sec
2
θ
d
θ
,
{\displaystyle x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,}
θ
=
arctan
x
.
{\displaystyle \theta =\arctan x.}
Since
arctan
0
=
0
{\displaystyle \arctan 0=0}
arctan
1
=
π
/
4
,
{\displaystyle \arctan 1=\pi /4,}
∫
0
1
4
d
x
1
+
x
2
=
4
∫
0
1
d
x
1
+
x
2
=
4
∫
0
π
/
4
sec
2
θ
d
θ
1
+
tan
2
θ
=
4
∫
0
π
/
4
sec
2
θ
d
θ
sec
2
θ
=
4
∫
0
π
/
4
d
θ
=
(
4
θ
)
|
0
π
/
4
=
4
(
π
4
−
0
)
=
π
.
{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\&=4\int _{0}^{\pi /4}d\theta \\&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}
Meanwhile, direct application of the boundary terms to the formula for the antiderivative yields
∫
0
1
4
d
x
1
+
x
2
=
4
∫
0
1
d
x
1
+
x
2
=
4
[
1
1
arctan
x
1
]
0
1
=
4
(
arctan
x
)
|
0
1
=
4
(
arctan
1
−
arctan
0
)
=
4
(
π
4
−
0
)
=
π
,
{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\left_{0}^{1}\\&=4(\arctan x){\Bigg |}_{0}^{1}\\&=4(\arctan 1-\arctan 0)\\&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}
Example 2
The integral
∫
a
2
+
x
2
d
x
{\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}}
may be evaluated by letting
x
=
a
tan
θ
,
d
x
=
a
sec
2
θ
d
θ
,
θ
=
arctan
x
a
,
{\displaystyle x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},}
where
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\displaystyle {\sqrt {a^{2}}}=a,}
−
π
2
<
θ
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}}
sec
θ
>
0
{\displaystyle \sec \theta >0}
sec
2
θ
=
sec
θ
.
{\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta .}
Then,
∫
a
2
+
x
2
d
x
=
∫
a
2
+
a
2
tan
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
a
2
(
1
+
tan
2
θ
)
(
a
sec
2
θ
)
d
θ
=
∫
a
2
sec
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
(
a
sec
θ
)
(
a
sec
2
θ
)
d
θ
=
a
2
∫
sec
3
θ
d
θ
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\&=a^{2}\int \sec ^{3}\theta \,d\theta .\\\end{aligned}}}
integral of secant cubed may be evaluated using integration by parts . As a result,
∫
a
2
+
x
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
1
+
x
2
a
2
⋅
x
a
+
ln
|
1
+
x
2
a
2
+
x
a
|
)
+
C
=
1
2
(
x
a
2
+
x
2
+
a
2
ln
|
x
+
a
2
+
x
2
a
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
Case III: Integrands containing x − a
Let
x
=
a
sec
θ
,
{\displaystyle x=a\sec \theta ,}
sec
2
θ
−
1
=
tan
2
θ
.
{\displaystyle \sec ^{2}\theta -1=\tan ^{2}\theta .}
Examples of Case III
Geometric construction for Case III Integrals such as
∫
d
x
x
2
−
a
2
{\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}}
can also be evaluated by partial fractions rather than trigonometric substitutions. However, the integral
∫
x
2
−
a
2
d
x
{\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx}
cannot. In this case, an appropriate substitution is:
x
=
a
sec
θ
,
d
x
=
a
sec
θ
tan
θ
d
θ
,
θ
=
arcsec
x
a
,
{\displaystyle x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}
where
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\displaystyle {\sqrt {a^{2}}}=a,}
0
≤
θ
<
π
2
{\displaystyle 0\leq \theta <{\frac {\pi }{2}}}
x
>
0
,
{\displaystyle x>0,}
tan
θ
≥
0
{\displaystyle \tan \theta \geq 0}
tan
2
θ
=
tan
θ
.
{\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta .}
Then,
∫
x
2
−
a
2
d
x
=
∫
a
2
sec
2
θ
−
a
2
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
(
sec
2
θ
−
1
)
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
tan
2
θ
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
sec
θ
tan
2
θ
d
θ
=
a
2
∫
(
sec
θ
)
(
sec
2
θ
−
1
)
d
θ
=
a
2
∫
(
sec
3
θ
−
sec
θ
)
d
θ
.
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}}
One may evaluate the integral of the secant function by multiplying the numerator and denominator by
(
sec
θ
+
tan
θ
)
{\displaystyle (\sec \theta +\tan \theta )}
integral of secant cubed by parts. As a result,
∫
x
2
−
a
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
−
a
2
ln
|
sec
θ
+
tan
θ
|
+
C
=
a
2
2
(
sec
θ
tan
θ
−
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
x
a
⋅
x
2
a
2
−
1
−
ln
|
x
a
+
x
2
a
2
−
1
|
)
+
C
=
1
2
(
x
x
2
−
a
2
−
a
2
ln
|
x
+
x
2
−
a
2
a
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
When
π
2
<
θ
≤
π
,
{\displaystyle {\frac {\pi }{2}}<\theta \leq \pi ,}
x
<
0
{\displaystyle x<0}
tan
θ
≤
0
,
{\displaystyle \tan \theta \leq 0,}
tan
2
θ
=
−
tan
θ
{\displaystyle {\sqrt {\tan ^{2}\theta }}=-\tan \theta }
Substitutions that eliminate trigonometric functions
Substitution can be used to remove trigonometric functions.
For instance,
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
±
1
−
u
2
f
(
u
,
±
1
−
u
2
)
d
u
u
=
sin
(
x
)
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
∓
1
−
u
2
f
(
±
1
−
u
2
,
u
)
d
u
u
=
cos
(
x
)
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
2
1
+
u
2
f
(
2
u
1
+
u
2
,
1
−
u
2
1
+
u
2
)
d
u
u
=
tan
(
x
2
)
{\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\frac {x}{2}}\right)\\\end{aligned}}}
The last substitution is known as the Weierstrass substitution , which makes use of tangent half-angle formulas .
For example,
∫
4
cos
x
(
1
+
cos
x
)
3
d
x
=
∫
2
1
+
u
2
4
(
1
−
u
2
1
+
u
2
)
(
1
+
1
−
u
2
1
+
u
2
)
3
d
u
=
∫
(
1
−
u
2
)
(
1
+
u
2
)
d
u
=
∫
(
1
−
u
4
)
d
u
=
u
−
u
5
5
+
C
=
tan
x
2
−
1
5
tan
5
x
2
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}}
Hyperbolic substitution
Substitutions of hyperbolic functions can also be used to simplify integrals.
For example, to integrate
1
/
a
2
+
x
2
{\displaystyle 1/{\sqrt {a^{2}+x^{2}}}}
x
=
a
sinh
u
{\displaystyle x=a\sinh {u}}
d
x
=
a
cosh
u
d
u
{\displaystyle dx=a\cosh u\,du}
the identity
cosh
2
(
x
)
−
sinh
2
(
x
)
=
1
{\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1}
to find:
∫
d
x
a
2
+
x
2
=
∫
a
cosh
u
d
u
a
2
+
a
2
sinh
2
u
=
∫
cosh
u
d
u
1
+
sinh
2
u
=
∫
cosh
u
cosh
u
d
u
=
u
+
C
=
sinh
−
1
x
a
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\\&=\int {\frac {\cosh {u}\,du}{\sqrt {1+\sinh ^{2}{u}}}}\\&=\int {\frac {\cosh {u}}{\cosh u}}\,du\\&=u+C\\&=\sinh ^{-1}{\frac {x}{a}}+C.\end{aligned}}}
If desired, this result may be further transformed using other identities, such as using the relation
sinh
−
1
z
=
arsinh
z
=
ln
(
z
+
z
2
+
1
)
{\displaystyle \sinh ^{-1}{z}=\operatorname {arsinh} {z}=\ln(z+{\sqrt {z^{2}+1}})}
:
sinh
−
1
x
a
+
C
=
ln
(
x
a
+
x
2
a
2
+
1
)
+
C
=
ln
(
x
+
x
2
+
a
2
a
)
+
C
.
{\displaystyle {\begin{aligned}\sinh ^{-1}{\frac {x}{a}}+C&=\ln \left({\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}+1}}\,\right)+C\\&=\ln \left({\frac {x+{\sqrt {x^{2}+a^{2}}}}{a}}\,\right)+C.\end{aligned}}}
See also
References
Stewart, James (2008). Calculus: Early Transcendentals Brooks/Cole . ISBN 978-0-495-01166-8 Thomas, George B. ; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley . ISBN 978-0-321-58876-0 Stewart, James (2012). "Section 7.2: Trigonometric Integrals". Calculus - Early Transcendentals . United States: Cengage Learning. pp. 475–6. ISBN 978-0-538-49790-9 Boyadzhiev, Khristo N. "Hyperbolic Substitutions for Integrals" (PDF). Archived from the original (PDF) on 26 February 2020. Retrieved 4 March 2013.
Categories :




 and use the
and use the 



 and
and  We can choose
We can choose  to be the principal root of
to be the principal root of  and impose the restriction
and impose the restriction  by using the inverse sine function.
by using the inverse sine function.
 goes from
goes from  to
to  then
then  goes from
goes from  so
so  goes from
goes from  Then,
Then,

 to
to  which would have resulted in the negative of the actual value.
which would have resulted in the negative of the actual value.
 as before.
as before.

 where
where  and
and  by the range of arcsine, so that
by the range of arcsine, so that  and
and 

 with values in the range
with values in the range  Alternatively, apply the boundary terms directly to the formula for the antiderivative.
Alternatively, apply the boundary terms directly to the formula for the antiderivative.

 with the bounds determined using
with the bounds determined using 
 and
and 

 as before.
as before.
 and use the identity
and use the identity 




 with values in the range
with values in the range  Alternatively, apply the boundary terms directly to the formula for the antiderivative.
Alternatively, apply the boundary terms directly to the formula for the antiderivative.

 with the bounds determined using
with the bounds determined using 
 and
and 

 same as before.
same as before.


 and
and  by the range of arctangent, so that
by the range of arctangent, so that  and
and 
 The
The 
 and use the identity
and use the identity 



 by assuming
by assuming  so that
so that  and
and 

 and the
and the 
 which happens when
which happens when  given the range of arcsecant,
given the range of arcsecant,  meaning
meaning  instead in that case.
instead in that case.


 , introduce the substitution
, introduce the substitution  (and hence
(and hence  ), then use
), then use 


