| 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Simplectic honeycomb |
| Schläfli symbol | {3} = 0 |
| Coxeter diagram | |
| 4-face types | {3,3,3} t1{3,3,3} |
| Cell types | {3,3} t1{3,3} |
| Face types | {3} |
| Vertex figure |  t0,3{3,3,3} |
| Symmetry | ×2 |
| Properties | vertex-transitive |
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1.
Structure
Cells of the vertex figure are ten tetrahedrons and 20 triangular prisms, corresponding to the ten 5-cells and 20 rectified 5-cells that meet at each vertex. All the vertices lie in parallel realms in which they form alternated cubic honeycombs, the tetrahedra being either tops of the rectified 5-cell or the bases of the 5-cell, and the octahedra being the bottoms of the rectified 5-cell.
Alternate names
- Cyclopentachoric tetracomb
- Pentachoric-dispentachoric tetracomb
Projection by folding
The 5-cell honeycomb can be projected into the 2-dimensional square tiling by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
Two different aperiodic tilings with 5-fold symmetry can be obtained by projecting two-dimensional slices of the honeycomb: the Penrose tiling composed of rhombi, and the Tübingen triangle tiling composed of isosceles triangles.
A4 lattice
The vertex arrangement of the 5-cell honeycomb is called the A4 lattice, or 4-simplex lattice. The 20 vertices of its vertex figure, the runcinated 5-cell represent the 20 roots of the Coxeter group. It is the 4-dimensional case of a simplectic honeycomb.
The A
4 lattice is the union of five A4 lattices, and is the dual to the omnitruncated 5-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell




 ∪
∪ 


 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 = dual of
= dual of 




Related polytopes and honeycombs
The tops of the 5-cells in this honeycomb adjoin the bases of the 5-cells, and vice versa, in adjacent laminae (or layers); but alternating laminae may be inverted so that the tops of the rectified 5-cells adjoin the tops of the rectified 5-cells and the bases of the 5-cells adjoin the bases of other 5-cells. This inversion results in another non-Wythoffian uniform convex honeycomb. Octahedral prisms and tetrahedral prisms may be inserted in between alternated laminae as well, resulting in two more non-Wythoffian elongated uniform honeycombs.
This honeycomb is one of seven unique uniform honeycombs constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| A4 honeycombs | ||||
|---|---|---|---|---|
| Pentagon symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| a1 | (None) | |||
| i2 | ] | ×2 | ||
| r10 | ] | ×10 | ||
Rectified 5-cell honeycomb
| Rectified 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,2{3} or r{3} |
| Coxeter diagram | |
| 4-face types | t1{3} t0,2{3} t0,3{3} |
| Cell types | Tetrahedron Octahedron Cuboctahedron Triangular prism |
| Vertex figure | triangular elongated-antiprismatic prism |
| Symmetry | ×2 |
| Properties | vertex-transitive |
The rectified 4-simplex honeycomb or rectified 5-cell honeycomb is a space-filling tessellation honeycomb.
Alternate names
- small cyclorhombated pentachoric tetracomb
- small prismatodispentachoric tetracomb
Cyclotruncated 5-cell honeycomb
| Cyclotruncated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Truncated simplectic honeycomb |
| Schläfli symbol | t0,1{3} |
| Coxeter diagram | |
| 4-face types | {3,3,3} t{3,3,3} 2t{3,3,3} |
| Cell types | {3,3} t{3,3} |
| Face types | Triangle {3} Hexagon {6} |
| Vertex figure | 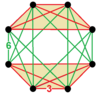 Tetrahedral antiprism , order 48 |
| Symmetry | ×2 |
| Properties | vertex-transitive |
The cyclotruncated 4-simplex honeycomb or cyclotruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a birectified 5-cell honeycomb.
It is composed of 5-cells, truncated 5-cells, and bitruncated 5-cells facets in a ratio of 2:2:1. Its vertex figure is a tetrahedral antiprism, with 2 regular tetrahedron, 8 triangular pyramid, and 6 tetragonal disphenoid cells, defining 2 5-cell, 8 truncated 5-cell, and 6 bitruncated 5-cell facets around a vertex.
It can be constructed as five sets of parallel hyperplanes that divide space into two half-spaces. The 3-space hyperplanes contain quarter cubic honeycombs as a collection facets.
Alternate names
- Cyclotruncated pentachoric tetracomb
- Small truncated-pentachoric tetracomb
Truncated 5-cell honeycomb
| Truncated 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,2{3} or t{3} |
| Coxeter diagram | |
| 4-face types | t0,1{3} t0,1,2{3} t0,3{3} |
| Cell types | Tetrahedron Truncated tetrahedron Truncated octahedron Triangular prism |
| Vertex figure | triangular elongated-antiprismatic pyramid |
| Symmetry | ×2 |
| Properties | vertex-transitive |
The truncated 4-simplex honeycomb or truncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cyclocantitruncated 5-cell honeycomb.
Alaternate names
- Great cyclorhombated pentachoric tetracomb
- Great truncated-pentachoric tetracomb
Cantellated 5-cell honeycomb
| Cantellated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,3{3} or rr{3} |
| Coxeter diagram | |
| 4-face types | t0,2{3} t1,2{3} t0,1,3{3} |
| Cell types | Truncated tetrahedron Octahedron Cuboctahedron Triangular prism Hexagonal prism |
| Vertex figure | Bidiminished rectified pentachoron |
| Symmetry | ×2 |
| Properties | vertex-transitive |
The cantellated 4-simplex honeycomb or cantellated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncitruncated 5-cell honeycomb.
Alternate names
- Cycloprismatorhombated pentachoric tetracomb
- Great prismatodispentachoric tetracomb
Bitruncated 5-cell honeycomb
| Bitruncated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,2,3{3} or 2t{3} |
| Coxeter diagram | |
| 4-face types | t0,1,3{3} t0,1,2{3} t0,1,2,3{3} |
| Cell types | Cuboctahedron Truncated octahedron |
| Vertex figure | tilted rectangular duopyramid |
| Symmetry | ×2 |
| Properties | vertex-transitive |
The bitruncated 4-simplex honeycomb or bitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncicantitruncated 5-cell honeycomb.
Alternate names
- Great cycloprismated pentachoric tetracomb
- Grand prismatodispentachoric tetracomb
Omnitruncated 5-cell honeycomb
| Omnitruncated 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Omnitruncated simplectic honeycomb |
| Schläfli symbol | t0,1,2,3,4{3} or tr{3} |
| Coxeter diagram | |
| 4-face types | t0,1,2,3{3,3,3} |
| Cell types | t0,1,2{3,3} {6}x{} |
| Face types | {4} {6} |
| Vertex figure |  Irr. 5-cell |
| Symmetry | ×10, ] |
| Properties | vertex-transitive, cell-transitive |
The omnitruncated 4-simplex honeycomb or omnitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a cyclosteriruncicantitruncated 5-cell honeycomb. .
It is composed entirely of omnitruncated 5-cell (omnitruncated 4-simplex) facets.
Coxeter calls this Hinton's honeycomb after C. H. Hinton, who described it in his book The Fourth Dimension in 1906.
The facets of all omnitruncated simplectic honeycombs are called permutohedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).
Alternate names
- Omnitruncated cyclopentachoric tetracomb
- Great-prismatodecachoric tetracomb
A4 lattice
The A
4 lattice is the union of five A4 lattices, and is the dual to the omnitruncated 5-cell honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell.




 ∪
∪ 


 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 = dual of
= dual of 




Alternated form
This honeycomb can be alternated, creating omnisnub 5-cells with irregular 5-cells created at the deleted vertices. Although it is not uniform, the 5-cells have a symmetry of order 10.
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
Notes
- Olshevsky (2006), Model 134
- Baake, M.; Kramer, P.; Schlottmann, M.; Zeidler, D. (December 1990). "Planar Patterns with Fivefold Symmetry as Sections of Periodic Structures in 4-Space". International Journal of Modern Physics B. 04 (15n16): 2217–2268. doi:10.1142/S0217979290001054.
- "The Lattice A4".
- "A4 root lattice - Wolfram|Alpha".
- "The Lattice A4".
- Olshevsky (2006), Klitzing, elong( x3o3o3o3o3*a ) - ecypit - O141, schmo( x3o3o3o3o3*a ) - zucypit - O142, elongschmo( x3o3o3o3o3*a ) - ezucypit - O143
- mathworld: Necklace, OEIS sequence A000029 8-1 cases, skipping one with zero marks
- Olshevsky, (2006) Model 135
- The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678. (The classification of Zonohededra, page 73)
- The Lattice A4*
References
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 134
- Klitzing, Richard. "4D Euclidean tesselations"., x3o3o3o3o3*a - cypit - O134, x3x3x3x3x3*a - otcypit - 135, x3x3x3o3o3*a - gocyropit - O137, x3x3o3x3o3*a - cypropit - O138, x3x3x3x3o3*a - gocypapit - O139, x3x3x3x3x3*a - otcypit - 140
- Affine Coxeter group Wa(A4), Quaternions, and Decagonal Quasicrystals, Mehmet Koca, Nazife O. Koca, Ramazan Koc (2013) arXiv:1209.1878
| Fundamental convex regular and uniform honeycombs in dimensions 2–9 | ||||||
|---|---|---|---|---|---|---|
| Space | Family | / / | ||||
| E | Uniform tiling | 0 | δ3 | hδ3 | qδ3 | Hexagonal |
| E | Uniform convex honeycomb | 0 | δ4 | hδ4 | qδ4 | |
| E | Uniform 4-honeycomb | 0 | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E | Uniform 5-honeycomb | 0 | δ6 | hδ6 | qδ6 | |
| E | Uniform 6-honeycomb | 0 | δ7 | hδ7 | qδ7 | 222 |
| E | Uniform 7-honeycomb | 0 | δ8 | hδ8 | qδ8 | 133 • 331 |
| E | Uniform 8-honeycomb | 0 | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E | Uniform 9-honeycomb | 0 | δ10 | hδ10 | qδ10 | |
| E | Uniform 10-honeycomb | 0 | δ11 | hδ11 | qδ11 | |
| E | Uniform (n-1)-honeycomb | 0 | δn | hδn | qδn | 1k2 • 2k1 • k21 |
 ×2
×2





 /
/  /
/ 