Competitive equilibrium (also called: Walrasian equilibrium) is a concept of economic equilibrium, introduced by Kenneth Arrow and Gérard Debreu in 1951, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated.
Definitions
A competitive equilibrium (CE) consists of two elements:
- A price function . It takes as argument a vector representing a bundle of commodities, and returns a positive real number that represents its price. Usually the price function is linear - it is represented as a vector of prices, a price for each commodity type.
- An allocation matrix . For every , is the vector of commodities allotted to agent .
These elements should satisfy the following requirement:
- Satisfaction (market-envy-freeness): Every agent weakly prefers his bundle to any other affordable bundle:
- , if then .
Often, there is an initial endowment matrix : for every , is the initial endowment of agent . Then, a CE should satisfy some additional requirements:
- Market Clearance: the demand equals the supply, no items are created or destroyed:
- .
- Individual Rationality: all agents are better-off after the trade than before the trade:
- .
- Budget Balance: all agents can afford their allocation given their endowment:
- .
Definition 2
This definition explicitly allows for the possibility that there may be multiple commodity arrays that are equally appealing. Also for zero prices. An alternative definition relies on the concept of a demand-set. Given a price function P and an agent with a utility function U, a certain bundle of goods x is in the demand-set of the agent if: for every other bundle y. A competitive equilibrium is a price function P and an allocation matrix X such that:
- The bundle allocated by X to each agent is in that agent's demand-set for the price-vector P;
- Every good which has a positive price is fully allocated (i.e. every unallocated item has price 0).
Approximate equilibrium
In some cases it is useful to define an equilibrium in which the rationality condition is relaxed. Given a positive value (measured in monetary units, e.g., dollars), a price vector and a bundle , define as a price vector in which all items in x have the same price they have in P, and all items not in x are priced more than their price in P.
In a -competitive-equilibrium, the bundle x allocated to an agent should be in that agent's demand-set for the modified price vector, .
This approximation is realistic when there are buy/sell commissions. For example, suppose that an agent has to pay dollars for buying a unit of an item, in addition to that item's price. That agent will keep his current bundle as long as it is in the demand-set for price vector . This makes the equilibrium more stable.
Examples
The following examples involve an exchange economy with two agents, Jane and Kelvin, two goods e.g. bananas (x) and apples (y), and no money.
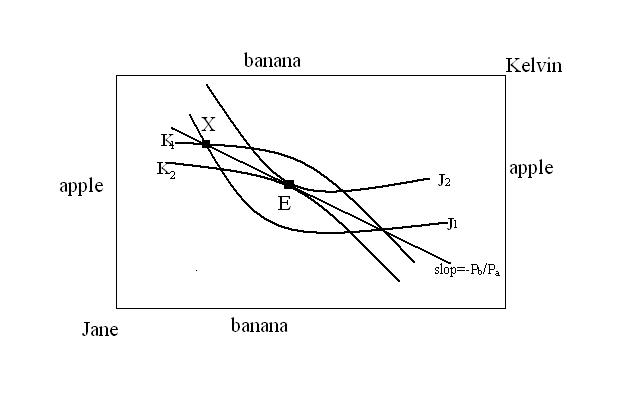
1. Graphical example: Suppose that the initial allocation is at point X, where Jane has more apples than Kelvin does and Kelvin has more bananas than Jane does.
By looking at their indifference curves of Jane and of Kelvin, we can see that this is not an equilibrium - both agents are willing to trade with each other at the prices and . After trading, both Jane and Kelvin move to an indifference curve which depicts a higher level of utility, and . The new indifference curves intersect at point E. The slope of the tangent of both curves equals -.
And the ; . The marginal rate of substitution (MRS) of Jane equals that of Kelvin. Therefore, the 2 individuals society reaches Pareto efficiency, where there is no way to make Jane or Kelvin better off without making the other worse off.
2. Arithmetic example: suppose that both agents have Cobb–Douglas utilities:
where are constants.
Suppose the initial endowment is .
The demand function of Jane for x is:
The demand function of Kelvin for x is:
The market clearance condition for x is:
This equation yields the equilibrium price ratio:
We could do a similar calculation for y, but this is not needed, since Walras' law guarantees that the results will be the same. Note that in CE, only relative prices are determined; we can normalize the prices, e.g, by requiring that . Then we get . But any other normalization will also work.
3. Non-existence example: Suppose the agents' utilities are:
and the initial endowment is . In CE, every agent must have either only x or only y (the other product does not contribute anything to the utility so the agent would like to exchange it away). Hence, the only possible CE allocations are and . Since the agents have the same income, necessarily . But then, the agent holding 2 units of y will want to exchange them for 4 units of x.
4. For existence and non-existence examples involving linear utilities, see Linear utility#Examples.
Indivisible items
When there are indivisible items in the economy, it is common to assume that there is also money, which is divisible. The agents have quasilinear utility functions: their utility is the amount of money they have plus the utility from the bundle of items they hold.
A. Single item: Alice has a car which she values as 10. Bob has no car, and he values Alice's car as 20. A possible CE is: the price of the car is 15, Bob gets the car and pays 15 to Alice. This is an equilibrium because the market is cleared and both agents prefer their final bundle to their initial bundle. In fact, every price between 10 and 20 will be a CE price, with the same allocation. The same situation holds when the car is not initially held by Alice but rather in an auction in which both Alice and Bob are buyers: the car will go to Bob and the price will be anywhere between 10 and 20.
On the other hand, any price below 10 is not an equilibrium price because there is an excess demand (both Alice and Bob want the car at that price), and any price above 20 is not an equilibrium price because there is an excess supply (neither Alice nor Bob want the car at that price).
This example is a special case of a double auction.
B. Substitutes: A car and a horse are sold in an auction. Alice only cares about transportation, so for her these are perfect substitutes: she gets utility 8 from the horse, 9 from the car, and if she has both of them then she uses only the car so her utility is 9. Bob gets a utility of 5 from the horse and 7 from the car, but if he has both of them then his utility is 11 since he also likes the horse as a pet. In this case it is more difficult to find an equilibrium (see below). A possible equilibrium is that Alice buys the horse for 5 and Bob buys the car for 7. This is an equilibrium since Bob wouldn't like to pay 5 for the horse which will give him only 4 additional utility, and Alice wouldn't like to pay 7 for the car which will give her only 1 additional utility.
C. Complements: A horse and a carriage are sold in an auction. There are two potential buyers: AND and XOR. AND wants only the horse and the carriage together - they receive a utility of from holding both of them but a utility of 0 for holding only one of them. XOR wants either the horse or the carriage but doesn't need both - they receive a utility of from holding one of them and the same utility for holding both of them. Here, when , a competitive equilibrium does NOT exist, i.e, no price will clear the market. Proof: consider the following options for the sum of the prices (horse-price + carriage-price):
- The sum is less than . Then, AND wants both items. Since the price of at least one item is less than , XOR wants that item, so there is excess demand.
- The sum is exactly . Then, AND is indifferent between buying both items and not buying any item. But XOR still wants exactly one item, so there is either excess demand or excess supply.
- The sum is more than . Then, AND wants no item and XOR still wants at most a single item, so there is excess supply.
D. Unit-demand consumers: There are n consumers. Each consumer has an index . There is a single type of good. Each consumer wants at most a single unit of the good, which gives him a utility of . The consumers are ordered such that is a weakly increasing function of . If the supply is units, then any price satisfying is an equilibrium price, since there are k consumers that either want to buy the product or indifferent between buying and not buying it. Note that an increase in supply causes a decrease in price.
Existence of a competitive equilibrium
Divisible resources
The Arrow–Debreu model shows that a CE exists in every exchange economy with divisible goods satisfying the following conditions:
- All agents have strictly convex preferences;
- All goods are desirable. This means that, if any good is given for free (), then all agents want as much as possible from that good.
The proof proceeds in several steps.
A. For concreteness, assume that there are agents and divisible goods. Normalize the prices such that their sum is 1, i.e. . Then the space of all possible prices is the -dimensional unit simplex in . We call this simplex the price simplex.
B. Let be the excess demand function. This is a function of the price vector when the initial endowment is kept constant:
It is known that, when the agents have strictly convex preferences, the Marshallian demand function is continuous. Hence, is also a continuous function of .
C. Define the following function from the price simplex to itself:
This is a continuous function, so by the Brouwer fixed-point theorem there is a price vector such that:
so,
D. Using Walras' law and some algebra, it is possible to show that for this price vector, there is no excess demand in any product, i.e:
E. The desirability assumption implies that all products have strictly positive prices:
By Walras' law, . But this implies that the inequality above must be an equality:
This means that is a price vector of a competitive equilibrium.
Note that Linear utilities are only weakly convex, so they do not qualify for the Arrow–Debreu model. However, David Gale proved that a CE exists in every linear exchange economy satisfying certain conditions. For details see Linear utilities#Existence of competitive equilibrium.
Algorithms for computing the market equilibrium are described in market equilibrium computation.
Indivisible items
In the examples above, a competitive equilibrium existed when the items were substitutes but not when the items were complements. This is not a coincidence.
Given a utility function on two goods X and Y, say that the goods are weakly gross-substitute (GS) if they are either independent goods or gross substitute goods, but not complementary goods. This means that . I.e., if the price of Y increases, then the demand for X either remains constant or increases, but does not decrease. If the price of Y decreases, then the demand for X either remains constant or decreases.
A utility function is called GS if, according to this utility function, all pairs of different goods are GS. With a GS utility function, if an agent has a demand set at a given price vector, and the prices of some items increase, then the agent has a demand set which includes all the items whose price remained constant. He may decide that he doesn't want an item which has become more expensive; he may also decide that he wants another item instead (a substitute); but he may not decide that he doesn't want a third item whose price hasn't changed.
When the utility functions of all agents are GS, a competitive equilibrium always exists.
Moreover, the set of GS valuations is the largest set containing unit demand valuations for which the existence of competitive equilibrium is guaranteed: for any non-GS valuation, there exist unit-demand valuations such that a competitive equilibrium does not exist for these unit-demand valuations coupled with the given non-GS valuation.
For the computational problem of finding a competitive equilibrium in a special kind of a market, see Fisher market#indivisible.
The competitive equilibrium and allocative efficiency
By the fundamental theorems of welfare economics, any CE allocation is Pareto efficient, and any efficient allocation can be sustainable by a competitive equilibrium. Furthermore, by Varian's theorems, a CE allocation in which all agents have the same income is also envy-free.
At the competitive equilibrium, the value society places on a good is equivalent to the value of the resources given up to produce it (marginal benefit equals marginal cost). This ensures allocative efficiency: the additional value society places on another unit of the good is equal to what society must give up in resources to produce it.
Note that microeconomic analysis does not assume additive utility, nor does it assume any interpersonal utility tradeoffs. Efficiency, therefore, refers to the absence of Pareto improvements. It does not in any way opine on the fairness of the allocation (in the sense of distributive justice or equity). An efficient equilibrium could be one where one player has all the goods and other players have none (in an extreme example), which is efficient in the sense that one may not be able to find a Pareto improvement - which makes all players (including the one with everything in this case) better off (for a strict Pareto improvement), or not worse off.
Welfare theorems for indivisible item assignment
In the case of indivisible items, we have the following strong versions of the two welfare theorems:
- Any competitive equilibrium maximizes the social welfare (the sum of utilities), not only over all realistic assignments of items, but also over all fractional assignments of items. I.e., even if we could assign fractions of an item to different people, we couldn't do better than a competitive equilibrium in which only whole items are assigned.
- If there is an integral assignment (with no fractional assignments) that maximizes the social welfare, then there is a competitive equilibrium with that assignment.
Finding an equilibrium
In the case of indivisible item assignment, when the utility functions of all agents are GS (and thus an equilibrium exists), it is possible to find a competitive equilibrium using an ascending auction. In an ascending auction, the auctioneer publishes a price vector, initially zero, and the buyers declare their favorite bundle under these prices. In case each item is desired by at most a single bidder, the items are divided and the auction is over. In case there is an excess demand on one or more items, the auctioneer increases the price of an over-demanded item by a small amount (e.g. a dollar), and the buyers bid again.
Several different ascending-auction mechanisms have been suggested in the literature. Such mechanisms are often called Walrasian auction, Walrasian tâtonnement or English auction.
See also
- Envy-free pricing - a relaxation of Walrasian equilibrium in which some items may remain unallocated.
- Fisher market - a simplified market model, with a single seller and many buyers, in which a CE can be computed efficiently.
- Allocative efficiency
- Economic equilibrium
- General equilibrium theory
- Walrasian auction
References
- K. Arrow, ‘An Extension of the Basic Theorems of Classical Welfare Economics’ (1951); G. Debreu, ‘The Coefficient of Resource Utilization’ (1951)
- ^ Liad Blumrosen and Noam Nisam (2007). "Combinatorial Auctions / Walrasian Equilibrium". In Nisan, Noam; Roughgarden, Tim; Tardos, Eva; Vazirani, Vijay (eds.). Algorithmic Game Theory (PDF). pp. 277–279. ISBN 978-0521872829.
- ^ Liad Blumrosen and Noam Nisam (2007). "Combinatorial Auctions / Ascending Auctions". In Nisan, Noam; Roughgarden, Tim; Tardos, Eva; Vazirani, Vijay (eds.). Algorithmic Game Theory (PDF). pp. 289–294. ISBN 978-0521872829.
- ^ Varian, Hal (1992). Microeconomic Analysis (Third ed.). New York: Norton. ISBN 0-393-95735-7.
- Hassidim, Avinatan; Kaplan, Haim; Mansour, Yishay; Nisan, Noam (2011). "Non-price equilibria in markets of discrete goods". Proceedings of the 12th ACM conference on Electronic commerce - EC '11. p. 295. arXiv:1103.3950. doi:10.1145/1993574.1993619. ISBN 9781450302616.
- The term was introduced at: Kelso, A. S.; Crawford, V. P. (1982). "Job Matching, Coalition Formation, and Gross Substitutes". Econometrica. 50 (6): 1483. doi:10.2307/1913392. JSTOR 1913392.
- ^ Gul, F.; Stacchetti, E. (2000). "The English Auction with Differentiated Commodities". Journal of Economic Theory. 92: 66–95. doi:10.1006/jeth.1999.2580.
- Gul, F.; Stacchetti, E. (1999). "Walrasian Equilibrium with Gross Substitutes". Journal of Economic Theory. 87: 95–124. doi:10.1006/jeth.1999.2531.
- Callan, S.J & Thomas, J.M. (2007). 'Modelling the Market Process: A Review of the Basics', Chapter 2 in Environmental Economics and Management: Theory, Politics and Applications, 4th ed., Thompson Southwestern, Mason, OH, USA
- Ben-Zwi, Oren; Lavi, Ron; Newman, Ilan (2013). "Ascending auctions and Walrasian equilibrium". arXiv:1301.1153v3 .
- Richter, M. K.; Wong, K. C. (1999). "Non-computability of competitive equilibrium". Economic Theory. 14: 1–27. doi:10.1007/s001990050281. S2CID 121248813.
External links
- Competitive equilibrium, Walrasian equilibrium and Walrasian auction in Economics Stack Exchange.
 . It takes as argument a vector representing a bundle of commodities, and returns a positive real number that represents its price. Usually the price function is linear - it is represented as a vector of prices, a price for each commodity type.
. It takes as argument a vector representing a bundle of commodities, and returns a positive real number that represents its price. Usually the price function is linear - it is represented as a vector of prices, a price for each commodity type. . For every
. For every  ,
,  is the vector of commodities allotted to agent
is the vector of commodities allotted to agent  .
. , if
, if  then
then  .
. : for every
: for every  is the initial endowment of agent
is the initial endowment of agent  .
. .
. .
. for every other bundle y. A competitive equilibrium is a price function P and an allocation matrix X such that:
for every other bundle y. A competitive equilibrium is a price function P and an allocation matrix X such that:
 (measured in monetary units, e.g., dollars), a price vector
(measured in monetary units, e.g., dollars), a price vector  , define
, define  as a price vector in which all items in x have the same price they have in P, and all items not in x are priced
as a price vector in which all items in x have the same price they have in P, and all items not in x are priced  of Jane and
of Jane and  of Kelvin, we can see that this is not an equilibrium - both agents are willing to trade with each other at the prices
of Kelvin, we can see that this is not an equilibrium - both agents are willing to trade with each other at the prices  and
and  . After trading, both Jane and Kelvin move to an indifference curve which depicts a higher level of utility,
. After trading, both Jane and Kelvin move to an indifference curve which depicts a higher level of utility,  and
and  . The new indifference curves intersect at point E. The slope of the tangent of both curves equals -
. The new indifference curves intersect at point E. The slope of the tangent of both curves equals - .
.
 ;
;
 .
The
.
The 

 are constants.
are constants.
 .
.




 . Then we get
. Then we get  . But any other normalization will also work.
. But any other normalization will also work.

 . But then, the agent holding 2 units of y will want to exchange them for 4 units of x.
. But then, the agent holding 2 units of y will want to exchange them for 4 units of x.
 from holding both of them but a utility of 0 for holding only one of them. XOR wants either the horse or the carriage but doesn't need both - they receive a utility of
from holding both of them but a utility of 0 for holding only one of them. XOR wants either the horse or the carriage but doesn't need both - they receive a utility of  from holding one of them and the same utility for holding both of them. Here, when
from holding one of them and the same utility for holding both of them. Here, when  , a competitive equilibrium does NOT exist, i.e, no price will clear the market. Proof: consider the following options for the sum of the prices (horse-price + carriage-price):
, a competitive equilibrium does NOT exist, i.e, no price will clear the market. Proof: consider the following options for the sum of the prices (horse-price + carriage-price):
 . There is a single type of good. Each consumer
. There is a single type of good. Each consumer  . The consumers are ordered such that
. The consumers are ordered such that  is a weakly increasing function of
is a weakly increasing function of  units, then any price
units, then any price  satisfying
satisfying  is an equilibrium price, since there are k consumers that either want to buy the product or indifferent between buying and not buying it. Note that an increase in supply causes a decrease in price.
is an equilibrium price, since there are k consumers that either want to buy the product or indifferent between buying and not buying it. Note that an increase in supply causes a decrease in price.
 is given for free (
is given for free ( ), then all agents want as much as possible from that good.
), then all agents want as much as possible from that good. agents and
agents and  divisible goods.
divisible goods.  . Then the space of all possible prices is the
. Then the space of all possible prices is the  -dimensional
-dimensional  . We call this simplex the price simplex.
. We call this simplex the price simplex.
 be the
be the 

 such that:
such that:




 . But this implies that the inequality above must be an equality:
. But this implies that the inequality above must be an equality:

 . I.e., if the price of Y increases, then the demand for X either remains constant or increases, but does not decrease. If the price of Y decreases, then the demand for X either remains constant or decreases.
. I.e., if the price of Y increases, then the demand for X either remains constant or increases, but does not decrease. If the price of Y decreases, then the demand for X either remains constant or decreases.