In numerical analysis, polynomial interpolation is the interpolation of a given bivariate data set by the polynomial of lowest possible degree that passes through the points of the dataset.
Given a set of n + 1 data points , with no two the same, a polynomial function is said to interpolate the data if for each .
There is always a unique such polynomial, commonly given by two explicit formulas, the Lagrange polynomials and Newton polynomials.
Applications
The original use of interpolation polynomials was to approximate values of important transcendental functions such as natural logarithm and trigonometric functions. Starting with a few accurately computed data points, the corresponding interpolation polynomial will approximate the function at an arbitrary nearby point. Polynomial interpolation also forms the basis for algorithms in numerical quadrature (Simpson's rule) and numerical ordinary differential equations (multigrid methods).
In computer graphics, polynomials can be used to approximate complicated plane curves given a few specified points, for example the shapes of letters in typography. This is usually done with Bézier curves, which are a simple generalization of interpolation polynomials (having specified tangents as well as specified points).
In numerical analysis, polynomial interpolation is essential to perform sub-quadratic multiplication and squaring, such as Karatsuba multiplication and Toom–Cook multiplication, where interpolation through points on a product polynomial yields the specific product required. For example, given a = f(x) = a0x + a1x + ··· and b = g(x) = b0x + b1x + ···, the product ab is a specific value of W(x) = f(x)g(x). One may easily find points along W(x) at small values of x, and interpolation based on those points will yield the terms of W(x) and the specific product ab. As fomulated in Karatsuba multiplication, this technique is substantially faster than quadratic multiplication, even for modest-sized inputs, especially on parallel hardware.
In computer science, polynomial interpolation also leads to algorithms for secure multi party computation and secret sharing.
Interpolation theorem
For any bivariate data points , where no two are the same, there exists a unique polynomial of degree at most that interpolates these points, i.e. .
Equivalently, for a fixed choice of interpolation nodes , polynomial interpolation defines a linear bijection between the (n+1)-tuples of real-number values and the vector space of real polynomials of degree at most n:
This is a type of unisolvence theorem. The theorem is also valid over any infinite field in place of the real numbers , for example the rational or complex numbers.
First proof
Consider the Lagrange basis functions given by:
Notice that is a polynomial of degree , and we have for each , while . It follows that the linear combination: has , so is an interpolating polynomial of degree .
To prove uniqueness, assume that there exists another interpolating polynomial of degree at most , so that for all . Then is a polynomial of degree at most which has distinct zeros (the ). But a non-zero polynomial of degree at most can have at most zeros, so must be the zero polynomial, i.e. .
Second proof
Write out the interpolation polynomial in the form
| 1 |
Substituting this into the interpolation equations , we get a system of linear equations in the coefficients , which reads in matrix-vector form as the following multiplication:
An interpolant corresponds to a solution of the above matrix equation . The matrix X on the left is a Vandermonde matrix, whose determinant is known to be which is non-zero since the nodes are all distinct. This ensures that the matrix is invertible and the equation has the unique solution ; that is, exists and is unique.
Corollary
If is a polynomial of degree at most , then the interpolating polynomial of at distinct points is itself.
Constructing the interpolation polynomial
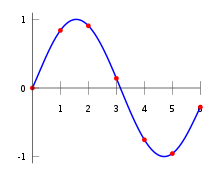
Lagrange Interpolation
Main article: Lagrange polynomialWe may write down the polynomial immediately in terms of Lagrange polynomials as: For matrix arguments, this formula is called Sylvester's formula and the matrix-valued Lagrange polynomials are the Frobenius covariants.
Newton Interpolation
See also: Newton polynomial and Divided differencesTheorem
For a polynomial of degree less than or equal to n, that interpolates at the nodes where . Let be the polynomial of degree less than or equal to n+1 that interpolates at the nodes where . Then is given by:where also known as Newton basis and .
Proof:
This can be shown for the case where :and when :By the uniqueness of interpolated polynomials of degree less than , is the required polynomial interpolation. The function can thus be expressed as:
Polynomial coefficients
To find , we have to solve the lower triangular matrix formed by arranging from above equation in matrix form:
The coefficients are derived as
where
is the notation for divided differences. Thus, Newton polynomials are used to provide a polynomial interpolation formula of n points.
| Proof |
|---|
|
The first few coefficients can be calculated using the system of equations. The form of n-th coefficient is assumed for proof by mathematical induction.
Let Q be polynomial interpolation of points . Adding to the polynomial Q:
where . By uniqueness of the interpolating polynomial of the points , equating the coefficients of we get, . Hence the polynomial can be expressed as: Adding to the polynomial Q, it has to satisfiy: where the formula for and interpolating polynomial are used. The term for the polynomial can be found by calculating:which implies that . Hence it is proved by principle of mathematical induction. |
Newton forward formula
The Newton polynomial can be expressed in a simplified form when are arranged consecutively with equal spacing.
If are consecutively arranged and equally spaced with for i = 0, 1, ..., k and some variable x is expressed as , then the difference can be written as . So the Newton polynomial becomes
Since the relationship between divided differences and forward differences is given as:Taking , if the representation of x in the previous sections was instead taken to be , the Newton forward interpolation formula is expressed as:which is the interpolation of all points after . It is expanded as:
Newton backward formula
If the nodes are reordered as , the Newton polynomial becomes
If are equally spaced with for i = 0, 1, ..., k and , then,
Since the relationship between divided differences and backward differences is given as:taking , if the representation of x in the previous sections was instead taken to be , the Newton backward interpolation formula is expressed as:which is the interpolation of all points before . It is expanded as:
Lozenge Diagram
A Lozenge diagram is a diagram that is used to describe different interpolation formulas that can be constructed for a given data set. A line starting on the left edge and tracing across the diagram to the right can be used to represent an interpolation formula if the following rules are followed:

- Left to right steps indicate addition whereas right to left steps indicate subtraction
- If the slope of a step is positive, the term to be used is the product of the difference and the factor immediately below it. If the slope of a step is negative, the term to be used is the product of the difference and the factor immediately above it.
- If a step is horizontal and passes through a factor, use the product of the factor and the average of the two terms immediately above and below it. If a step is horizontal and passes through a difference, use the product of the difference and the average of the two terms immediately above and below it.
The factors are expressed using the formula:
Proof of equivalence
If a path goes from to , it can connect through three intermediate steps, (a) through , (b) through or (c) through . Proving the equivalence of these three two-step paths should prove that all (n-step) paths can be morphed with the same starting and ending, all of which represents the same formula.
Path (a):
Path (b):
Path (c):
Subtracting contributions from path a and b:
Thus, the contribution of either path (a) or path (b) is the same. Since path (c) is the average of path (a) and (b), it also contributes identical function to the polynomial. Hence the equivalence of paths with same starting and ending points is shown. To check if the paths can be shifted to different values in the leftmost corner, taking only two step paths is sufficient: (a) to through or (b) factor between and , to through or (c) starting from .
Path (a)
Path (b)
Path (c)
Since , substituting in the above equations shows that all the above terms reduce to and are hence equivalent. Hence these paths can be morphed to start from the leftmost corner and end in a common point.
Newton formula
Taking negative slope transversal from to gives the interpolation formula of all the consecutively arranged points, equivalent to Newton's forward interpolation formula:
whereas, taking positive slope transversal from to , gives the interpolation formula of all the consecutively arranged points, equivalent to Newton's backward interpolation formula:
where is the number corresponding to that introduced in Newton interpolation.
Gauss formula
Taking a zigzag line towards the right starting from with negative slope, we get Gauss forward formula:
whereas starting from with positive slope, we get Gauss backward formula:
Stirling formula
By taking a horizontal path towards the right starting from , we get Stirling formula:
Stirling formula is the average of Gauss forward and Gauss backward formulas.
Bessel formula
By taking a horizontal path towards the right starting from factor between and , we get Stirling formula:
Vandermonde Algorithms
The Vandermonde matrix in the second proof above may have large condition number, causing large errors when computing the coefficients ai if the system of equations is solved using Gaussian elimination.
Several authors have therefore proposed algorithms which exploit the structure of the Vandermonde matrix to compute numerically stable solutions in O(n) operations instead of the O(n) required by Gaussian elimination. These methods rely on constructing first a Newton interpolation of the polynomial and then converting it to a monomial form.
Non-Vandermonde algorithms
To find the interpolation polynomial p(x) in the vector space P(n) of polynomials of degree n, we may use the usual monomial basis for P(n) and invert the Vandermonde matrix by Gaussian elimination, giving a computational cost of O(n) operations. To improve this algorithm, a more convenient basis for P(n) can simplify the calculation of the coefficients, which must then be translated back in terms of the monomial basis.
One method is to write the interpolation polynomial in the Newton form (i.e. using Newton basis) and use the method of divided differences to construct the coefficients, e.g. Neville's algorithm. The cost is O(n) operations. Furthermore, you only need to do O(n) extra work if an extra point is added to the data set, while for the other methods, you have to redo the whole computation.
Another method is preferred when the aim is not to compute the coefficients of p(x), but only a single value p(a) at a point x = a not in the original data set. The Lagrange form computes the value p(a) with complexity O(n).
The Bernstein form was used in a constructive proof of the Weierstrass approximation theorem by Bernstein and has gained great importance in computer graphics in the form of Bézier curves.
Interpolations as linear combinations of values
Given a set of (position, value) data points where no two positions are the same, the interpolating polynomial may be considered as a linear combination of the values , using coefficients which are polynomials in depending on the . For example, the interpolation polynomial in the Lagrange form is the linear combination with each coefficient given by the corresponding Lagrange basis polynomial on the given positions :
Since the coefficients depend only on the positions , not the values , we can use the same coefficients to find the interpolating polynomial for a second set of data points at the same positions:
Furthermore, the coefficients only depend on the relative spaces between the positions. Thus, given a third set of data whose points are given by the new variable (an affine transformation of , inverted by ):
we can use a transformed version of the previous coefficient polynomials:
and write the interpolation polynomial as:
Data points often have equally spaced positions, which may be normalized by an affine transformation to . For example, consider the data points
.
The interpolation polynomial in the Lagrange form is the linear combination
For example, and .
The case of equally spaced points can also be treated by the method of finite differences. The first difference of a sequence of values is the sequence defined by . Iterating this operation gives the n difference operation , defined explicitly by:where the coefficients form a signed version of Pascal's triangle, the triangle of binomial transform coefficients:
| 1 | Row n = 0 | ||||||||||||||||
| 1 | −1 | Row n = 1 or d = 0 | |||||||||||||||
| 1 | −2 | 1 | Row n = 2 or d = 1 | ||||||||||||||
| 1 | −3 | 3 | −1 | Row n = 3 or d = 2 | |||||||||||||
| 1 | −4 | 6 | −4 | 1 | Row n = 4 or d = 3 | ||||||||||||
| 1 | −5 | 10 | −10 | 5 | −1 | Row n = 5 or d = 4 | |||||||||||
| 1 | −6 | 15 | −20 | 15 | −6 | 1 | Row n = 6 or d = 5 | ||||||||||
| 1 | −7 | 21 | −35 | 35 | −21 | 7 | −1 | Row n = 7 or d = 6 | |||||||||
A polynomial of degree d defines a sequence of values at positive integer points, , and the difference of this sequence is identically zero:
.
Thus, given values at equally spaced points, where , we have: For example, 4 equally spaced data points of a quadratic obey , and solving for gives the same interpolation equation obtained above using the Lagrange method.
Interpolation error: Lagrange remainder formula
| This section may be confusing or unclear to readers. Please help clarify the section. There might be a discussion about this on the talk page. (June 2011) (Learn how and when to remove this message) |
When interpolating a given function f by a polynomial of degree n at the nodes x0,..., xn we get the error
where is the (n+1) divided difference of the data points
.
Furthermore, there is a Lagrange remainder form of the error, for a function f which is n + 1 times continuously differentiable on a closed interval , and a polynomial of degree at most n that interpolates f at n + 1 distinct points . For each there exists such that
This error bound suggests choosing the interpolation points xi to minimize the product , which is achieved by the Chebyshev nodes.
Proof of Lagrange remainder
Set the error term as , and define an auxiliary function:Thus:
But since is a polynomial of degree at most n, we have , and:
Now, since xi are roots of and , we have , which means Y has at least n + 2 roots. From Rolle's theorem, has at least n + 1 roots, and iteratively has at least one root ξ in the interval I. Thus:
and:
This parallels the reasoning behind the Lagrange remainder term in the Taylor theorem; in fact, the Taylor remainder is a special case of interpolation error when all interpolation nodes xi are identical. Note that the error will be zero when for any i. Thus, the maximum error will occur at some point in the interval between two successive nodes.
Equally spaced intervals
In the case of equally spaced interpolation nodes where , for and where the product term in the interpolation error formula can be bound as
Thus the error bound can be given as
However, this assumes that is dominated by , i.e. . In several cases, this is not true and the error actually increases as n → ∞ (see Runge's phenomenon). That question is treated in the section Convergence properties.
Lebesgue constants
Main article: Lebesgue constantWe fix the interpolation nodes x0, ..., xn and an interval containing all the interpolation nodes. The process of interpolation maps the function f to a polynomial p. This defines a mapping X from the space C() of all continuous functions on to itself. The map X is linear and it is a projection on the subspace of polynomials of degree n or less.
The Lebesgue constant L is defined as the operator norm of X. One has (a special case of Lebesgue's lemma):
In other words, the interpolation polynomial is at most a factor (L + 1) worse than the best possible approximation. This suggests that we look for a set of interpolation nodes that makes L small. In particular, we have for Chebyshev nodes:
We conclude again that Chebyshev nodes are a very good choice for polynomial interpolation, as the growth in n is exponential for equidistant nodes. However, those nodes are not optimal.
Convergence properties
It is natural to ask, for which classes of functions and for which interpolation nodes the sequence of interpolating polynomials converges to the interpolated function as n → ∞? Convergence may be understood in different ways, e.g. pointwise, uniform or in some integral norm.
The situation is rather bad for equidistant nodes, in that uniform convergence is not even guaranteed for infinitely differentiable functions. One classical example, due to Carl Runge, is the function f(x) = 1 / (1 + x) on the interval . The interpolation error || f − pn||∞ grows without bound as n → ∞. Another example is the function f(x) = |x| on the interval , for which the interpolating polynomials do not even converge pointwise except at the three points x = ±1, 0.
One might think that better convergence properties may be obtained by choosing different interpolation nodes. The following result seems to give a rather encouraging answer:
Theorem — For any function f(x) continuous on an interval there exists a table of nodes for which the sequence of interpolating polynomials converges to f(x) uniformly on .
ProofIt is clear that the sequence of polynomials of best approximation converges to f(x) uniformly (due to the Weierstrass approximation theorem). Now we have only to show that each may be obtained by means of interpolation on certain nodes. But this is true due to a special property of polynomials of best approximation known from the equioscillation theorem. Specifically, we know that such polynomials should intersect f(x) at least n + 1 times. Choosing the points of intersection as interpolation nodes we obtain the interpolating polynomial coinciding with the best approximation polynomial.
The defect of this method, however, is that interpolation nodes should be calculated anew for each new function f(x), but the algorithm is hard to be implemented numerically. Does there exist a single table of nodes for which the sequence of interpolating polynomials converge to any continuous function f(x)? The answer is unfortunately negative:
Theorem — For any table of nodes there is a continuous function f(x) on an interval for which the sequence of interpolating polynomials diverges on .
The proof essentially uses the lower bound estimation of the Lebesgue constant, which we defined above to be the operator norm of Xn (where Xn is the projection operator on Πn). Now we seek a table of nodes for which
Due to the Banach–Steinhaus theorem, this is only possible when norms of Xn are uniformly bounded, which cannot be true since we know that
For example, if equidistant points are chosen as interpolation nodes, the function from Runge's phenomenon demonstrates divergence of such interpolation. Note that this function is not only continuous but even infinitely differentiable on . For better Chebyshev nodes, however, such an example is much harder to find due to the following result:
Theorem — For every absolutely continuous function on the sequence of interpolating polynomials constructed on Chebyshev nodes converges to f(x) uniformly.
Related concepts
Runge's phenomenon shows that for high values of n, the interpolation polynomial may oscillate wildly between the data points. This problem is commonly resolved by the use of spline interpolation. Here, the interpolant is not a polynomial but a spline: a chain of several polynomials of a lower degree.
Interpolation of periodic functions by harmonic functions is accomplished by Fourier transform. This can be seen as a form of polynomial interpolation with harmonic base functions, see trigonometric interpolation and trigonometric polynomial.
Hermite interpolation problems are those where not only the values of the polynomial p at the nodes are given, but also all derivatives up to a given order. This turns out to be equivalent to a system of simultaneous polynomial congruences, and may be solved by means of the Chinese remainder theorem for polynomials. Birkhoff interpolation is a further generalization where only derivatives of some orders are prescribed, not necessarily all orders from 0 to a k.
Collocation methods for the solution of differential and integral equations are based on polynomial interpolation.
The technique of rational function modeling is a generalization that considers ratios of polynomial functions.
At last, multivariate interpolation for higher dimensions.
See also
Notes
- This follows from the Factor theorem for polynomial division.
Citations
- Tiemann, Jerome J. (May–June 1981). "Polynomial Interpolation". I/O News. 1 (5): 16. ISSN 0274-9998. Retrieved 3 November 2017.
- Humpherys, Jeffrey; Jarvis, Tyler J. (2020). "9.2 - Interpolation". Foundations of Applied Mathematics Volume 2: Algorithms, Approximation, Optimization. Society for Industrial and Applied Mathematics. p. 418. ISBN 978-1-611976-05-2.
- ^ Epperson, James F. (2013). An introduction to numerical methods and analysis (2nd ed.). Hoboken, NJ: Wiley. ISBN 978-1-118-36759-9.
- Burden, Richard L.; Faires, J. Douglas (2011). Numerical Analysis (9th ed.). Cengage Learning. p. 129. ISBN 9780538733519.
- ^ Hamming, Richard W. (1986). Numerical methods for scientists and engineers (Unabridged republ. of the 2. ed. (1973) ed.). New York: Dover. ISBN 978-0-486-65241-2.
- Gautschi, Walter (1975). "Norm Estimates for Inverses of Vandermonde Matrices". Numerische Mathematik. 23 (4): 337–347. doi:10.1007/BF01438260. S2CID 122300795.
- Higham, N. J. (1988). "Fast Solution of Vandermonde-Like Systems Involving Orthogonal Polynomials". IMA Journal of Numerical Analysis. 8 (4): 473–486. doi:10.1093/imanum/8.4.473.
- Björck, Å; V. Pereyra (1970). "Solution of Vandermonde Systems of Equations". Mathematics of Computation. 24 (112). American Mathematical Society: 893–903. doi:10.2307/2004623. JSTOR 2004623.
- Calvetti, D.; Reichel, L. (1993). "Fast Inversion of Vandermonde-Like Matrices Involving Orthogonal Polynomials". BIT. 33 (3): 473–484. doi:10.1007/BF01990529. S2CID 119360991.
- R.Bevilaqua, D. Bini, M.Capovani and O. Menchi (2003). Appunti di Calcolo Numerico. Chapter 5, p. 89. Servizio Editoriale Universitario Pisa - Azienda Regionale Diritto allo Studio Universitario.
- "Errors in Polynomial Interpolation" (PDF).
- "Notes on Polynomial Interpolation" (PDF).
- Watson (1980, p. 21) attributes the last example to Bernstein (1912).
- Watson (1980, p. 21) attributes this theorem to Faber (1914).
- Krylov, V. I. (1956). "Сходимость алгебраического интерполирования покорням многочленов Чебышева для абсолютно непрерывных функций и функций с ограниченным изменением" [Convergence of algebraic interpolation with respect to the roots of Chebyshev's polynomial for absolutely continuous functions and functions of bounded variation]. Doklady Akademii Nauk SSSR. New Series (in Russian). 107: 362–365. MR 18-32.
References
- Bernstein, Sergei N. (1912). "Sur l'ordre de la meilleure approximation des fonctions continues par les polynômes de degré donné" [On the order of the best approximation of continuous functions by polynomials of a given degree]. Mem. Acad. Roy. Belg. (in French). 4: 1–104.
- Faber, Georg (1914). "Über die interpolatorische Darstellung stetiger Funktionen" [On the Interpolation of Continuous Functions]. Deutsche Math. Jahr. (in German). 23: 192–210.
- Watson, G. Alistair (1980). Approximation Theory and Numerical Methods. John Wiley. ISBN 0-471-27706-1.
Further reading
- Atkinson, Kendell A. (1988). "Chapter 3.". An Introduction to Numerical Analysis (2nd ed.). John Wiley and Sons. ISBN 0-471-50023-2.
- Brutman, L. (1997). "Lebesgue functions for polynomial interpolation — a survey". Ann. Numer. Math. 4: 111–127.
- Powell, M. J. D. (1981). "Chapter 4". Approximation Theory and Methods. Cambridge University Press. ISBN 0-521-29514-9.
- Schatzman, Michelle (2002). "Chapter 4". Numerical Analysis: A Mathematical Introduction. Oxford: Clarendon Press. ISBN 0-19-850279-6.
- Süli, Endre; Mayers, David (2003). "Chapter 6". An Introduction to Numerical Analysis. Cambridge University Press. ISBN 0-521-00794-1.
- J. L. Walsh: Interpolation and Approximation by Rational Functions in the Complex Domain, AMS (Colloquium Publications, Vol.20), ISBN 0-8218-1020-0 (1960). Chapter VII:'Interpolation by Polynomials'.
External links
- "Interpolation process", Encyclopedia of Mathematics, EMS Press, 2001
- ALGLIB has an implementations in C++ / C#.
- GSL has a polynomial interpolation code in C
- Polynomial Interpolation demonstration.
 , with no two
, with no two  the same, a polynomial function
the same, a polynomial function  is said to interpolate the data if
is said to interpolate the data if  for each
for each  .
.
 bivariate data points
bivariate data points  , where no two
, where no two  of degree at most
of degree at most  that interpolates these points, i.e.
that interpolates these points, i.e.  .
.
 between the (n+1)-tuples of real-number values
between the (n+1)-tuples of real-number values  and the
and the  of real polynomials of degree at most n:
of real polynomials of degree at most n:

 , for example the rational or complex numbers.
, for example the rational or complex numbers.
 given by:
given by:

 is a polynomial of degree
is a polynomial of degree  for each
for each  , while
, while  . It follows that the linear combination:
. It follows that the linear combination:
 has
has  , so
, so  of degree at most
of degree at most  for all
for all  . Then
. Then  is a polynomial of degree at most
is a polynomial of degree at most  ). But a non-zero polynomial of degree at most
). But a non-zero polynomial of degree at most  .
.

 , which reads in matrix-vector form as the following
, which reads in matrix-vector form as the following 
 of the above matrix equation
of the above matrix equation  . The matrix X on the left is a
. The matrix X on the left is a  which is non-zero since the nodes
which is non-zero since the nodes  ; that is,
; that is,  is a polynomial of degree at most
is a polynomial of degree at most  For matrix arguments, this formula is called
For matrix arguments, this formula is called  of degree less than or equal to n, that interpolates
of degree less than or equal to n, that interpolates  at the nodes
at the nodes  where
where  . Let
. Let  be the polynomial of degree less than or equal to n+1 that interpolates
be the polynomial of degree less than or equal to n+1 that interpolates  . Then
. Then  where
where  also known as Newton basis and
also known as Newton basis and  .
.
 and when
and when  :
: By the uniqueness of interpolated polynomials of degree less than
By the uniqueness of interpolated polynomials of degree less than  is the required polynomial interpolation. The function can thus be expressed as:
is the required polynomial interpolation. The function can thus be expressed as:

 , we have to solve the
, we have to solve the  from above equation in matrix form:
from above equation in matrix form:




 . Adding
. Adding  to the polynomial Q:
to the polynomial Q:

 . By uniqueness of the interpolating polynomial of the points
. By uniqueness of the interpolating polynomial of the points  we get,
we get,  .
.

 to the polynomial Q, it has to satisfiy:
to the polynomial Q, it has to satisfiy:  where the formula for
where the formula for  and interpolating polynomial are used.
The
and interpolating polynomial are used.
The  term for the polynomial
term for the polynomial  can be found by calculating:
can be found by calculating: which implies that
which implies that  .
.
 are arranged consecutively with equal spacing.
are arranged consecutively with equal spacing.
 for i = 0, 1, ..., k and some variable x is expressed as
for i = 0, 1, ..., k and some variable x is expressed as  , then the difference
, then the difference  can be written as
can be written as  . So the Newton polynomial becomes
. So the Newton polynomial becomes

 Taking
Taking  , if the representation of x in the previous sections was instead taken to be
, if the representation of x in the previous sections was instead taken to be  , the Newton forward interpolation formula is expressed as:
, the Newton forward interpolation formula is expressed as: which is the interpolation of all points after
which is the interpolation of all points after 
 , the Newton polynomial becomes
, the Newton polynomial becomes

 are equally spaced with
are equally spaced with  for i = 0, 1, ..., k and
for i = 0, 1, ..., k and  , then,
, then,

 taking
taking  which is the interpolation of all points before
which is the interpolation of all points before 

 to
to  , it can connect through three intermediate steps, (a) through
, it can connect through three intermediate steps, (a) through  , (b) through
, (b) through  or (c) through
or (c) through  . Proving the equivalence of these three two-step paths should prove that all (n-step) paths can be morphed with the same starting and ending, all of which represents the same formula.
. Proving the equivalence of these three two-step paths should prove that all (n-step) paths can be morphed with the same starting and ending, all of which represents the same formula.




 to
to  through
through  or (b) factor between
or (b) factor between 

 , substituting in the above equations shows that all the above terms reduce to
, substituting in the above equations shows that all the above terms reduce to  to
to  gives the interpolation formula of all the
gives the interpolation formula of all the 
 to
to  , gives the interpolation formula of all the
, gives the interpolation formula of all the 
 is the number corresponding to that introduced in Newton interpolation.
is the number corresponding to that introduced in Newton interpolation.



 , we get Stirling formula:
, we get Stirling formula:

 where no two positions
where no two positions  may be considered as a
may be considered as a  , using coefficients which are polynomials in
, using coefficients which are polynomials in  depending on the
depending on the  with each coefficient
with each coefficient  given by the corresponding Lagrange basis polynomial on the given positions
given by the corresponding Lagrange basis polynomial on the given positions 
 at the same positions:
at the same positions:

 between the positions. Thus, given a third set of data whose points are given by the new variable
between the positions. Thus, given a third set of data whose points are given by the new variable  (an
(an  ):
):



 often have equally spaced positions, which may be normalized by an affine transformation to
often have equally spaced positions, which may be normalized by an affine transformation to  . For example, consider the data points
. For example, consider the data points .
.
 and
and  .
.
 is the sequence
is the sequence  defined by
defined by  . Iterating this operation gives the n difference operation
. Iterating this operation gives the n difference operation  , defined explicitly by:
, defined explicitly by: where the coefficients form a signed version of Pascal's triangle, the
where the coefficients form a signed version of Pascal's triangle, the  , and the
, and the  difference of this sequence is identically zero:
difference of this sequence is identically zero:  .
.  at equally spaced points, where
at equally spaced points, where  , we have:
, we have:  For example, 4 equally spaced data points
For example, 4 equally spaced data points  of a quadratic
of a quadratic  , and solving for
, and solving for  gives the same interpolation equation obtained above using the Lagrange method.
gives the same interpolation equation obtained above using the Lagrange method.

 is the (n+1)
is the (n+1)  .
. , and a polynomial
, and a polynomial  of degree at most n that interpolates f at n + 1 distinct points
of degree at most n that interpolates f at n + 1 distinct points  . For each
. For each  there exists
there exists  such that
such that

 , which is achieved by the
, which is achieved by the  , and define an auxiliary function:
, and define an auxiliary function: Thus:
Thus:
 , and:
, and:

 and
and  , we have
, we have  , which means Y has at least n + 2 roots. From
, which means Y has at least n + 2 roots. From  has at least n + 1 roots, and iteratively
has at least n + 1 roots, and iteratively  has at least one root ξ in the interval I. Thus:
has at least one root ξ in the interval I. Thus:


 for any i. Thus, the maximum error will occur at some point in the interval between two successive nodes.
for any i. Thus, the maximum error will occur at some point in the interval between two successive nodes.
 , for
, for  and where
and where  the product term in the interpolation error formula can be bound as
the product term in the interpolation error formula can be bound as


 is dominated by
is dominated by  , i.e.
, i.e.  . In several cases, this is not true and the error actually increases as n → ∞ (see
. In several cases, this is not true and the error actually increases as n → ∞ (see 

 converges to f(x) uniformly (due to the
converges to f(x) uniformly (due to the 
