Misplaced Pages

Square root of 3

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (April 2024) (Learn how and when to remove this message)
Unique positive real number which when multiplied by itself gives 3
Square root of 3
The height of an equilateral triangle with sides of length 2 equals the square root of 3.
Representations
Decimal1.7320508075688772935...
Continued fraction 1 + 1 1 + 1 2 + 1 1 + 1 2 + 1 1 + ⋱ {\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}}

The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as 3 {\textstyle {\sqrt {3}}} or 3 1 / 2 {\displaystyle 3^{1/2}} . It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality.

In 2013, its numerical value in decimal notation was computed to ten billion digits. Its decimal expansion, written here to 65 decimal places, is given by OEIS: A002194:

1.732050807568877293527446341505872366942805253810380628055806

The fraction 97 56 {\textstyle {\frac {97}{56}}} (1.732142857...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than 1 10 , 000 {\textstyle {\frac {1}{10,000}}} (approximately 9.2 × 10 − 5 {\textstyle 9.2\times 10^{-5}} , with a relative error of 5 × 10 − 5 {\textstyle 5\times 10^{-5}} ). The rounded value of 1.732 is correct to within 0.01% of the actual value.

The fraction 716 , 035 413 , 403 {\textstyle {\frac {716,035}{413,403}}} (1.73205080756...) is accurate to 1 × 10 − 11 {\textstyle 1\times 10^{-11}} .

Archimedes reported a range for its value: ( 1351 780 ) 2 > 3 > ( 265 153 ) 2 {\textstyle ({\frac {1351}{780}})^{2}>3>({\frac {265}{153}})^{2}} .

The lower limit 1351 780 {\textstyle {\frac {1351}{780}}} is an accurate approximation for 3 {\displaystyle {\sqrt {3}}} to 1 608 , 400 {\textstyle {\frac {1}{608,400}}} (six decimal places, relative error 3 × 10 − 7 {\textstyle 3\times 10^{-7}} ) and the upper limit 265 153 {\textstyle {\frac {265}{153}}} to 2 23 , 409 {\textstyle {\frac {2}{23,409}}} (four decimal places, relative error 1 × 10 − 5 {\textstyle 1\times 10^{-5}} ).

Expressions

It can be expressed as the simple continued fraction (sequence A040001 in the OEIS).

So it is true to say:

[ 1 2 1 3 ] n = [ a 11 a 12 a 21 a 22 ] {\displaystyle {\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}}

then when n → ∞ {\displaystyle n\to \infty }  :

3 = 2 ⋅ a 22 a 12 − 1 {\displaystyle {\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1}

Geometry and trigonometry

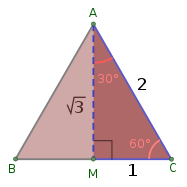The height of an equilateral triangle with edge length 2 is √3. Also, the long leg of a 30-60-90 triangle with hypotenuse 2.And, the height of a regular hexagon with sides of length 1.
The space diagonal of the unit cube is √3.
Distances between vertices of a double unit cube are square roots of the first six natural numbers, including the square root of 3 (√7 is not possible due to Legendre's three-square theorem)
This projection of the Bilinski dodecahedron is a rhombus with diagonal ratio √3.

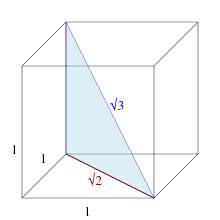
The square root of 3 can be found as the leg length of an equilateral triangle that encompasses a circle with a diameter of 1.

If an equilateral triangle with sides of length 1 is cut into two equal halves, by bisecting an internal angle across to make a right angle with one side, the right angle triangle's hypotenuse is length one, and the sides are of length 1 2 {\textstyle {\frac {1}{2}}} and 3 2 {\textstyle {\frac {\sqrt {3}}{2}}} . From this, tan ⁡ 60 ∘ = 3 {\textstyle \tan {60^{\circ }}={\sqrt {3}}} , sin ⁡ 60 ∘ = 3 2 {\textstyle \sin {60^{\circ }}={\frac {\sqrt {3}}{2}}} , and cos ⁡ 30 ∘ = 3 2 {\textstyle \cos {30^{\circ }}={\frac {\sqrt {3}}{2}}} .

The square root of 3 also appears in algebraic expressions for various other trigonometric constants, including the sines of 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, and 87°.

It is the distance between parallel sides of a regular hexagon with sides of length 1.

It is the length of the space diagonal of a unit cube.

The vesica piscis has a major axis to minor axis ratio equal to 1 : 3 {\displaystyle 1:{\sqrt {3}}} . This can be shown by constructing two equilateral triangles within it.

Other uses and occurrence

Power engineering

In power engineering, the voltage between two phases in a three-phase system equals 3 {\textstyle {\sqrt {3}}} times the line to neutral voltage. This is because any two phases are 120° apart, and two points on a circle 120 degrees apart are separated by 3 {\textstyle {\sqrt {3}}} times the radius (see geometry examples above).

Special functions

It is known that most roots of the nth derivatives of J ν ( n ) ( x ) {\displaystyle J_{\nu }^{(n)}(x)} (where n < 18 and J ν ( x ) {\displaystyle J_{\nu }(x)} is the Bessel function of the first kind of order ν {\displaystyle \nu } ) are transcendental. The only exceptions are the numbers ± 3 {\displaystyle \pm {\sqrt {3}}} , which are the algebraic roots of both J 1 ( 3 ) ( x ) {\displaystyle J_{1}^{(3)}(x)} and J 0 ( 4 ) ( x ) {\displaystyle J_{0}^{(4)}(x)} .

References

  1. Komsta, Łukasz (December 2013). "Computations | Łukasz Komsta". komsta.net. WordPress. Archived from the original on 2023-10-02. Retrieved September 24, 2016.
  2. Knorr, Wilbur R. (June 1976). "Archimedes and the measurement of the circle: a new interpretation". Archive for History of Exact Sciences. 15 (2): 115–140. doi:10.1007/bf00348496. JSTOR 41133444. MR 0497462. S2CID 120954547. Retrieved November 15, 2022 – via SpringerLink.
  3. Wiseman, Julian D. A. (June 2008). "Sin and Cos in Surds". JDAWiseman.com. Retrieved November 15, 2022.
  4. Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions". International Journal of Mathematics and Mathematical Sciences. 18 (3): 551–560. doi:10.1155/S0161171295000706.
  • Podestá, Ricardo A. (2020). "A geometric proof that sqrt 3, sqrt 5, and sqrt 7 are irrational". arXiv:2003.06627 .

Further reading

External links

Algebraic numbers
icon Mathematics portal
Irrational numbers
Categories:
Square root of 3 Add topic