Misplaced Pages

Small dodecicosidodecahedron
Type	Uniform star polyhedron
Elements	F = 44, E = 120 V = 60 (χ = −16)
Faces by sides	20{3}+12{5}+12{10}
Coxeter diagram
Wythoff symbol	3/2 5 | 5 3 5/4 | 5
Symmetry group	Ih, , *532
Index references	U33, C42, W72
Dual polyhedron	Small dodecacronic hexecontahedron
Vertex figure	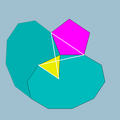5.10.3/2.10
Bowers acronym	Saddid

In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U₃₃. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

Related polyhedra

It shares its vertex arrangement with the small stellated truncated dodecahedron and the uniform compounds of 6 or 12 pentagrammic prisms. It additionally shares its edge arrangement with the rhombicosidodecahedron (having the triangular and pentagonal faces in common), and with the small rhombidodecahedron (having the decagonal faces in common).

Rhombicosidodecahedron	Small dodecicosidodecahedron	Small rhombidodecahedron
Small stellated truncated dodecahedron	Compound of six pentagrammic prisms	Compound of twelve pentagrammic prisms

Dual

Small dodecacronic hexecontahedron
Type	Star polyhedron
Face
Elements	F = 60, E = 120 V = 44 (χ = −16)
Symmetry group	Ih, , *532
Index references	DU33
dual polyhedron	Small dodecicosidodecahedron

The dual polyhedron to the small dodecicosidodecahedron is the small dodecacronic hexecontahedron (or small sagittal ditriacontahedron). It is visually identical to the small rhombidodecacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

Proportions

Faces have two angles of ${\displaystyle \arccos({\frac {5}{8}}+{\frac {1}{8}}{\sqrt {5}})\approx 25.242\,832\,961\,52^{\circ }}$, one of ${\displaystyle \arccos(-{\frac {1}{8}}+{\frac {9}{40}}{\sqrt {5}})\approx 67.783\,011\,547\,44^{\circ }}$ and one of ${\displaystyle 360^{\circ }-\arccos(-{\frac {1}{4}}-{\frac {1}{10}}{\sqrt {5}})\approx 241.731\,322\,529\,52^{\circ }}$. Its dihedral angles equal ${\displaystyle \arccos({\frac {-19-8{\sqrt {5}}}{41}})\approx 154.121\,363\,125\,78^{\circ }}$. The ratio between the lengths of the long and short edges is ${\displaystyle {\frac {7+{\sqrt {5}}}{6}}\approx 1.539\,344\,662\,92}$.

References

1. Maeder, Roman. "33: small dodecicosidodecahedron". MathConsult.

• Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 246 (916): 401–450. doi:10.1098/rsta.1954.0003.
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208

External links

• Weisstein, Eric W. "Uniform Polyhedron". MathWorld.
• Weisstein, Eric W. "Small dodecicosidodecahedron". MathWorld.
• Weisstein, Eric W. "Small dodecacronic hexecontahedron". MathWorld.

This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Uniform polyhedra
• Polyhedron stubs