This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

 The signal on the left looks like noise, but the signal processing technique known as spectral density estimation (right) shows that it contains five well-defined frequency components.
The signal on the left looks like noise, but the signal processing technique known as spectral density estimation (right) shows that it contains five well-defined frequency components.
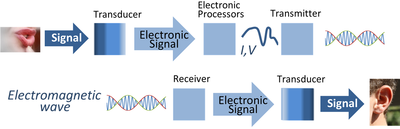
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing signals, such as sound, images, potential fields, seismic signals, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal.
History
According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s.
In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information communication systems and the processing of signals for transmission.
Signal processing matured and flourished in the 1960s and 1970s, and digital signal processing became widely used with specialized digital signal processor chips in the 1980s.
Definition of a signal
A signal is a function , where this function is either
- deterministic (then one speaks of a deterministic signal) or
- a path , a realization of a stochastic process
Categories
Analog
Main article: Analog signal processingAnalog signal processing is for signals that have not been digitized, as in most 20th-century radio, telephone, and television systems. This involves linear electronic circuits as well as nonlinear ones. The former are, for instance, passive filters, active filters, additive mixers, integrators, and delay lines. Nonlinear circuits include compandors, multipliers (frequency mixers, voltage-controlled amplifiers), voltage-controlled filters, voltage-controlled oscillators, and phase-locked loops.
Continuous time
Continuous-time signal processing is for signals that vary with the change of continuous domain (without considering some individual interrupted points).
The methods of signal processing include time domain, frequency domain, and complex frequency domain. This technology mainly discusses the modeling of a linear time-invariant continuous system, integral of the system's zero-state response, setting up system function and the continuous time filtering of deterministic signals. For example, in time domain, a continuous-time signal passing through a linear time-invariant filter/system denoted as , can be expressed at the output as
In some contexts, is referred to as the impulse response of the system. The above convolution operation is conducted between the input and the system.
Discrete time
Discrete-time signal processing is for sampled signals, defined only at discrete points in time, and as such are quantized in time, but not in magnitude.
Analog discrete-time signal processing is a technology based on electronic devices such as sample and hold circuits, analog time-division multiplexers, analog delay lines and analog feedback shift registers. This technology was a predecessor of digital signal processing (see below), and is still used in advanced processing of gigahertz signals.
The concept of discrete-time signal processing also refers to a theoretical discipline that establishes a mathematical basis for digital signal processing, without taking quantization error into consideration.
Digital
Main article: Digital signal processingDigital signal processing is the processing of digitized discrete-time sampled signals. Processing is done by general-purpose computers or by digital circuits such as ASICs, field-programmable gate arrays or specialized digital signal processors. Typical arithmetical operations include fixed-point and floating-point, real-valued and complex-valued, multiplication and addition. Other typical operations supported by the hardware are circular buffers and lookup tables. Examples of algorithms are the fast Fourier transform (FFT), finite impulse response (FIR) filter, Infinite impulse response (IIR) filter, and adaptive filters such as the Wiener and Kalman filters.
Nonlinear
Nonlinear signal processing involves the analysis and processing of signals produced from nonlinear systems and can be in the time, frequency, or spatiotemporal domains. Nonlinear systems can produce highly complex behaviors including bifurcations, chaos, harmonics, and subharmonics which cannot be produced or analyzed using linear methods.
Polynomial signal processing is a type of non-linear signal processing, where polynomial systems may be interpreted as conceptually straightforward extensions of linear systems to the nonlinear case.
Statistical
Statistical signal processing is an approach which treats signals as stochastic processes, utilizing their statistical properties to perform signal processing tasks. Statistical techniques are widely used in signal processing applications. For example, one can model the probability distribution of noise incurred when photographing an image, and construct techniques based on this model to reduce the noise in the resulting image.
Application fields

- Audio signal processing – for electrical signals representing sound, such as speech or music
- Image processing – in digital cameras, computers and various imaging systems
- Video processing – for interpreting moving pictures
- Wireless communication – waveform generations, demodulation, filtering, equalization
- Control systems
- Array processing – for processing signals from arrays of sensors
- Process control – a variety of signals are used, including the industry standard 4-20 mA current loop
- Seismology
- Feature extraction, such as image understanding and speech recognition.
- Quality improvement, such as noise reduction, image enhancement, and echo cancellation.
- Source coding including audio compression, image compression, and video compression.
- Genomic signal processing
- In geophysics, signal processing is used to amplify the signal vs the noise within time-series measurements of geophysical data. Processing is conducted within either the time domain or frequency domain, or both.
In communication systems, signal processing may occur at:
- OSI layer 1 in the seven-layer OSI model, the physical layer (modulation, equalization, multiplexing, etc.);
- OSI layer 2, the data link layer (forward error correction);
- OSI layer 6, the presentation layer (source coding, including analog-to-digital conversion and data compression).
Typical devices
- Filters – for example analog (passive or active) or digital (FIR, IIR, frequency domain or stochastic filters, etc.)
- Samplers and analog-to-digital converters for signal acquisition and reconstruction, which involves measuring a physical signal, storing or transferring it as digital signal, and possibly later rebuilding the original signal or an approximation thereof.
- Signal compressors
- Digital signal processors (DSPs)
Mathematical methods applied
- Differential equations - for modeling system behavior, connecting input and output relations in linear time-invariant systems. For instance, a low-pass filter such as an RC circuit can be modeled as a differential equation in signal processing, which allows one to compute the continuous output signal as function of the input or initial conditions.
- Recurrence relations
- Transform theory
- Time-frequency analysis – for processing non-stationary signals
- Linear canonical transformation
- Spectral estimation – for determining the spectral content (i.e., the distribution of power over frequency) of a time series
- Statistical signal processing – analyzing and extracting information from signals and noise based on their stochastic properties
- Linear time-invariant system theory, and transform theory
- Polynomial signal processing – analysis of systems which relate input and output using polynomials
- System identification and classification
- Calculus
- Code
- Complex analysis
- Vector spaces and Linear algebra
- Functional analysis
- Probability and stochastic processes
- Detection theory
- Estimation theory
- Optimization
- Numerical methods
- Time series
- Data mining – for statistical analysis of relations between large quantities of variables (in this context representing many physical signals), to extract previously unknown interesting patterns
See also
- Algebraic signal processing
- Audio filter
- Bounded variation
- Digital image processing
- Dynamic range compression, companding, limiting, and noise gating
- Fourier transform
- Information theory
- Least-squares spectral analysis
- Non-local means
- Reverberation
- Sensitivity (electronics)
- Similarity (signal processing)
References
- Sengupta, Nandini; Sahidullah, Md; Saha, Goutam (August 2016). "Lung sound classification using cepstral-based statistical features". Computers in Biology and Medicine. 75 (1): 118–129. doi:10.1016/j.compbiomed.2016.05.013. PMID 27286184.
- Alan V. Oppenheim and Ronald W. Schafer (1989). Discrete-Time Signal Processing. Prentice Hall. p. 1. ISBN 0-13-216771-9.
- Oppenheim, Alan V.; Schafer, Ronald W. (1975). Digital Signal Processing. Prentice Hall. p. 5. ISBN 0-13-214635-5.
- "A Mathematical Theory of Communication – CHM Revolution". Computer History. Retrieved 2019-05-13.
- ^ Fifty Years of Signal Processing: The IEEE Signal Processing Society and its Technologies, 1948–1998 (PDF). The IEEE Signal Processing Society. 1998.
- Berber, S. (2021). Discrete Communication Systems. United Kingdom: Oxford University Press., page 9, https://books.google.com/books?id=CCs0EAAAQBAJ&pg=PA9
- "Microwave & Millimeter-wave Circuits and Systems". Retrieved 2024-10-20.
- ^ Billings, S. A. (2013). Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains. Wiley. ISBN 978-1-119-94359-4.
- Slawinska, J.; Ourmazd, A.; Giannakis, D. (2018). "A New Approach to Signal Processing of Spatiotemporal Data". 2018 IEEE Statistical Signal Processing Workshop (SSP). IEEE Xplore. pp. 338–342. doi:10.1109/SSP.2018.8450704. ISBN 978-1-5386-1571-3. S2CID 52153144.
- V. John Mathews; Giovanni L. Sicuranza (May 2000). Polynomial Signal Processing. Wiley. ISBN 978-0-471-03414-8.
- ^ Scharf, Louis L. (1991). Statistical signal processing: detection, estimation, and time series analysis. Boston: Addison–Wesley. ISBN 0-201-19038-9. OCLC 61160161.
- Sarangi, Susanta; Sahidullah, Md; Saha, Goutam (September 2020). "Optimization of data-driven filterbank for automatic speaker verification". Digital Signal Processing. 104: 102795. arXiv:2007.10729. Bibcode:2020DSP...10402795S. doi:10.1016/j.dsp.2020.102795. S2CID 220665533.
- Anastassiou, D. (2001). "Genomic signal processing". IEEE Signal Processing Magazine. 18 (4). IEEE: 8–20. Bibcode:2001ISPM...18....8A. doi:10.1109/79.939833.
- Telford, William Murray; Geldart, L. P.; Sheriff, Robert E. (1990). Applied geophysics. Cambridge University Press. ISBN 978-0-521-33938-4.
- Reynolds, John M. (2011). An Introduction to Applied and Environmental Geophysics. Wiley-Blackwell. ISBN 978-0-471-48535-3.
- Patrick Gaydecki (2004). Foundations of Digital Signal Processing: Theory, Algorithms and Hardware Design. IET. pp. 40–. ISBN 978-0-85296-431-6.
- Shlomo Engelberg (8 January 2008). Digital Signal Processing: An Experimental Approach. Springer Science & Business Media. ISBN 978-1-84800-119-0.
- Boashash, Boualem, ed. (2003). Time frequency signal analysis and processing a comprehensive reference (1 ed.). Amsterdam: Elsevier. ISBN 0-08-044335-4.
- Stoica, Petre; Moses, Randolph (2005). Spectral Analysis of Signals (PDF). NJ: Prentice Hall.
- Peter J. Schreier; Louis L. Scharf (4 February 2010). Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals. Cambridge University Press. ISBN 978-1-139-48762-7.
- Max A. Little (13 August 2019). Machine Learning for Signal Processing: Data Science, Algorithms, and Computational Statistics. OUP Oxford. ISBN 978-0-19-102431-3.
- Steven B. Damelin; Willard Miller, Jr (2012). The Mathematics of Signal Processing. Cambridge University Press. ISBN 978-1-107-01322-3.
- Daniel P. Palomar; Yonina C. Eldar (2010). Convex Optimization in Signal Processing and Communications. Cambridge University Press. ISBN 978-0-521-76222-9.
Further reading
- P Stoica, R Moses (2005). Spectral Analysis of Signals (PDF). NJ: Prentice Hall.
- Kay, Steven M. (1993). Fundamentals of Statistical Signal Processing. Upper Saddle River, New Jersey: Prentice Hall. ISBN 0-13-345711-7. OCLC 26504848.
- Papoulis, Athanasios (1991). Probability, Random Variables, and Stochastic Processes (third ed.). McGraw-Hill. ISBN 0-07-100870-5.
- Kainam Thomas Wong : Statistical Signal Processing lecture notes at the University of Waterloo, Canada.
- Ali H. Sayed, Adaptive Filters, Wiley, NJ, 2008, ISBN 978-0-470-25388-5.
- Thomas Kailath, Ali H. Sayed, and Babak Hassibi, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4.
External links
- Signal Processing for Communications – free online textbook by Paolo Prandoni and Martin Vetterli (2008)
- Scientists and Engineers Guide to Digital Signal Processing – free online textbook by Stephen Smith
- Julius O. Smith III: Spectral Audio Signal Processing – free online textbook
| Digital signal processing | |
|---|---|
| Theory | |
| Sub-fields | |
| Techniques | |
| Sampling | |
 , where this function is either
, where this function is either
 , a realization of a
, a realization of a 
 , can be expressed at the output as
, can be expressed at the output as
