| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Nuclear chain reaction" – news · newspapers · books · scholar · JSTOR (October 2024) (Learn how and when to remove this message) |
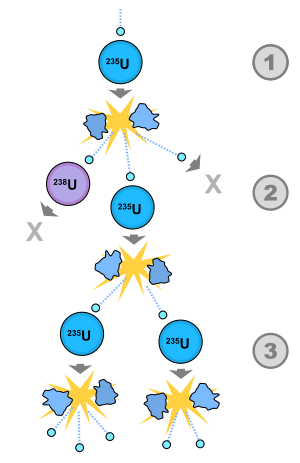
1) A uranium-235 atom absorbs a neutron and fissions into two fission fragments, releasing three new neutrons and a large amount of binding energy.
2) One of those neutrons is absorbed by an atom of uranium-238, and does not continue the reaction. Another neutron leaves the system without being absorbed. However, one neutron does collide with an atom of uranium-235, which then fissions and releases two neutrons and more binding energy.
3) Both of those neutrons collide with uranium-235 atoms, each of which fissions and releases a few neutrons, which can then continue the reaction.
In nuclear physics, a nuclear chain reaction occurs when one single nuclear reaction causes an average of one or more subsequent nuclear reactions, thus leading to the possibility of a self-propagating series or "positive feedback loop" of these reactions. The specific nuclear reaction may be the fission of heavy isotopes (e.g., uranium-235, U). A nuclear chain reaction releases several million times more energy per reaction than any chemical reaction.
History
Chemical chain reactions were first proposed by German chemist Max Bodenstein in 1913, and were reasonably well understood before nuclear chain reactions were proposed. It was understood that chemical chain reactions were responsible for exponentially increasing rates in reactions, such as produced in chemical explosions.
The concept of a nuclear chain reaction was reportedly first hypothesized by Hungarian scientist Leó Szilárd on September 12, 1933. Szilárd that morning had been reading in a London paper of an experiment in which protons from an accelerator had been used to split lithium-7 into alpha particles, and the fact that much greater amounts of energy were produced by the reaction than the proton supplied. Ernest Rutherford commented in the article that inefficiencies in the process precluded use of it for power generation. However, the neutron had been discovered by James Chadwick in 1932, shortly before, as the product of a nuclear reaction. Szilárd, who had been trained as an engineer and physicist, put the two nuclear experimental results together in his mind and realized that if a nuclear reaction produced neutrons, which then caused further similar nuclear reactions, the process might be a self-perpetuating nuclear chain reaction, spontaneously producing new isotopes and power without the need for protons or an accelerator. Szilárd, however, did not propose fission as the mechanism for his chain reaction since the fission reaction was not yet discovered, or even suspected. Instead, Szilárd proposed using mixtures of lighter known isotopes which produced neutrons in copious amounts. He filed a patent for his idea of a simple nuclear reactor the following year.
In 1936, Szilárd attempted to create a chain reaction using beryllium and indium but was unsuccessful. Nuclear fission was discovered by Otto Hahn and Fritz Strassmann in December 1938 and explained theoretically in January 1939 by Lise Meitner and her nephew Otto Robert Frisch. In their second publication on nuclear fission in February 1939, Hahn and Strassmann used the term uranspaltung (uranium fission) for the first time and predicted the existence and liberation of additional neutrons during the fission process, opening up the possibility of a nuclear chain reaction.
A few months later, Frédéric Joliot-Curie, H. Von Halban and L. Kowarski in Paris searched for, and discovered, neutron multiplication in uranium, proving that a nuclear chain reaction by this mechanism was indeed possible. On May 4, 1939, Joliot-Curie, Halban, and Kowarski filed three patents. The first two described power production from a nuclear chain reaction, the last one called Perfectionnement aux charges explosives was the first patent for the atomic bomb and is filed as patent No. 445686 by the Caisse nationale de Recherche Scientifique. In parallel, Szilárd and Enrico Fermi in New York made the same analysis. This discovery prompted the letter from Szilárd and signed by Albert Einstein to President Franklin D. Roosevelt, warning of the possibility that Nazi Germany might be attempting to build an atomic bomb.
On December 2, 1942, a team led by Fermi (and including Szilárd) produced the first artificial self-sustaining nuclear chain reaction with the Chicago Pile-1 experimental reactor in a racquets court below the bleachers of Stagg Field at the University of Chicago. Fermi's experiments at the University of Chicago were part of Arthur H. Compton's Metallurgical Laboratory of the Manhattan Project; the lab was renamed Argonne National Laboratory and tasked with conducting research in harnessing fission for nuclear energy.
In 1956, Paul Kuroda of the University of Arkansas postulated that a natural fission reactor may have once existed. Since nuclear chain reactions may only require natural materials (such as water and uranium, if the uranium has sufficient amounts of U), it was possible to have these chain reactions occur in the distant past when uranium-235 concentrations were higher than today, and where there was the right combination of materials within the Earth's crust. Uranium-235 made up a larger share of uranium on Earth in the geological past because of the different half-lives of the isotopes
U and
U, the former decaying almost an order of magnitude faster than the latter. Kuroda's prediction was verified with the discovery of evidence of natural self-sustaining nuclear chain reactions in the past at Oklo in Gabon in September 1972. To sustain a nuclear fission chain reaction at present isotope ratios in natural uranium on Earth would require the presence of a neutron moderator like heavy water or high purity carbon (e.g. graphite) in the absence of neutron poisons, which is even more unlikely to arise by natural geological processes than the conditions at Oklo some two billion years ago.
Process
Fission chain reactions occur because of interactions between neutrons and fissile isotopes (such as U). The chain reaction requires both the release of neutrons from fissile isotopes undergoing nuclear fission and the subsequent absorption of some of these neutrons in fissile isotopes. When an atom undergoes nuclear fission, a few neutrons (the exact number depends on uncontrollable and unmeasurable factors; the expected number depends on several factors, usually between 2.5 and 3.0) are ejected from the reaction. These free neutrons will then interact with the surrounding medium, and if more fissile fuel is present, some may be absorbed and cause more fissions. Thus, the cycle repeats to produce a reaction that is self-sustaining.
Nuclear power plants operate by precisely controlling the rate at which nuclear reactions occur. Nuclear weapons, on the other hand, are specifically engineered to produce a reaction that is so fast and intense it cannot be controlled after it has started. When properly designed, this uncontrolled reaction will lead to an explosive energy release.
Fuel
Main article: Nuclear fuelNuclear weapons employ high quality, highly enriched fuel exceeding the critical size and geometry (critical mass) necessary in order to obtain an explosive chain reaction. The fuel for energy purposes, such as in a nuclear fission reactor, is very different, usually consisting of a low-enriched oxide material (e.g. uranium dioxide, UO2). There are two primary isotopes used for fission reactions inside of nuclear reactors.
The first and most common is uranium-235. This is the fissile isotope of uranium and it makes up approximately 0.7% of all naturally occurring uranium. Because of the small amount of U that exists, it is considered a non-renewable energy source despite being found in rock formations around the world. Uranium-235 cannot be used as fuel in its base form for energy production; it must undergo a process known as refinement to produce the compound UO2. The UO2 is then pressed and formed into ceramic pellets, which can subsequently be placed into fuel rods. This is when UO2 can be used for nuclear power production.
The second most common isotope used in nuclear fission is plutonium-239, because it is able to become fissile with slow neutron interaction. This isotope is formed inside nuclear reactors by exposing U to the neutrons released during fission. As a result of neutron capture, uranium-239 is produced, which undergoes two beta decays to become plutonium-239. Plutonium once occurred as a primordial element in Earth's crust, but only trace amounts remain so it is predominantly synthetic.
Another proposed fuel for nuclear reactors, which however plays no commercial role as of 2021, is uranium-233, which is "bred" by neutron capture and subsequent beta decays from natural thorium, which is almost 100% composed of the isotope thorium-232. This is called the thorium fuel cycle.
Enrichment process
Main article: Enriched uraniumThe fissile isotope uranium-235 in its natural concentration is unfit for the vast majority of nuclear reactors. In order to be prepared for use as fuel in energy production, it must be enriched. The enrichment process does not apply to plutonium. Reactor-grade plutonium is created as a byproduct of neutron interaction between two different isotopes of uranium.
The first step to enriching uranium begins by converting uranium oxide (created through the uranium milling process) into a gaseous form. This gas is known as uranium hexafluoride, which is created by combining hydrogen fluoride, fluorine, and uranium oxide. Uranium dioxide is also present in this process and is sent off to be used in reactors not requiring enriched fuel. The remaining uranium hexafluoride compound is drained into metal cylinders where it solidifies. The next step is separating the uranium hexafluoride from the depleted U-235 left over. This is typically done with centrifuges that spin fast enough to allow for the 1% mass difference in uranium isotopes to separate themselves. A laser is then used to enrich the hexafluoride compound. The final step involves reconverting the enriched compound back into uranium oxide, leaving the final product: enriched uranium oxide. This form of UO2 can now be used in fission reactors inside power plants to produce energy.
Reaction products
When a fissile atom undergoes nuclear fission, it breaks into two or more fission fragments. Also, several free neutrons, gamma rays, and neutrinos are emitted, and a large amount of energy is released. The sum of the rest masses of the fission fragments and ejected neutrons is less than the sum of the rest masses of the original atom and incident neutron (of course the fission fragments are not at rest). The mass difference is accounted for in the release of energy according to the equation E=Δmc:
- mass of released energy =
Due to the extremely large value of the speed of light, c, a small decrease in mass is associated with a tremendous release of active energy (for example, the kinetic energy of the fission fragments). This energy (in the form of radiation and heat) carries the missing mass when it leaves the reaction system (total mass, like total energy, is always conserved). While typical chemical reactions release energies on the order of a few eVs (e.g. the binding energy of the electron to hydrogen is 13.6 eV), nuclear fission reactions typically release energies on the order of hundreds of millions of eVs.
Two typical fission reactions are shown below with average values of energy released and number of neutrons ejected:
Note that these equations are for fissions caused by slow-moving (thermal) neutrons. The average energy released and number of neutrons ejected is a function of the incident neutron speed. Also, note that these equations exclude energy from neutrinos since these subatomic particles are extremely non-reactive and therefore rarely deposit their energy in the system.
Reactor physics
Prompt neutron lifetime
The prompt neutron lifetime, , is the average time between the emission of a neutron and either its absorption or escape from the system. The neutrons that occur directly from fission are called prompt neutrons, and the ones that are a result of radioactive decay of fission fragments are called delayed neutrons. The term lifetime is used because the emission of a neutron is often considered its birth, and its subsequent absorption or escape from the core is considered its death.
For "thermal" (slow-neutron) fission reactors, the typical prompt neutron lifetime is on the order of 10 seconds, and for fast fission reactors, the prompt neutron lifetime is on the order of 10 seconds. These extremely short lifetimes mean that in 1 second, 10,000 to 10,000,000 neutron lifetimes can pass. The average (also referred to as the adjoint unweighted) prompt neutron lifetime takes into account all prompt neutrons regardless of their importance in the reactor core; the effective prompt neutron lifetime (referred to as the adjoint weighted over space, energy, and angle) refers to a neutron with average importance.
Mean generation time
The mean generation time, λ, is the average time from a neutron emission to a capture that results in fission. The mean generation time is different from the prompt neutron lifetime because the mean generation time only includes neutron absorptions that lead to fission reactions (not other absorption reactions). The two times are related by the following formula:
In this formula keff is the effective neutron multiplication factor, described below.
Effective neutron multiplication factor
The effective neutron multiplication factor is most often quantified as the ratio of the rate of neutron production to the rate of neutron loss in a nuclear system, and it is often described using the six-factor formula.
Using and the prompt neutron lifetime, , the following differential equation can be used to describe the time rate of change of the neutron population:
When solved for , this equation represents the neutron population at any given time given an initial neutron population at :
When describing a nuclear reactor, where neutron population is directly proportional to thermal power, the following equation is used:
where is the reactor power at time , given an initial power , and , the reactor period. The value of can be calculated as
Six-factor formula
The effective neutron multiplication factor can be described using the product of six probability factors that describe a nuclear system. These factors, traditionally arranged chronologically with regards to the life of a neutron in a thermal reactor, include the probability of fast non-leakage , the fast fission factor , the resonance escape probability , the probability of thermal non-leakage , the thermal utilization factor , and the neutron reproduction factor (also called the neutron efficiency factor). The six-factor formula is traditionally written as follows:
Where:
- describes the probability that a fast neutron will not escape the system without interacting.
- The bounds of this factor are 0 and 1, with a value of 1 describing a system for which fast neutrons will never escape without interacting, i.e. an infinite system.
- Also written as
- is the ratio of total fissions to fissions caused only by thermal neutrons
- Fast neutrons have a small probability to cause fissions in uranium, specifically uranium-238.
- The fast fission factor describes the contribution of fast fissions to the effective neutron multiplication factor
- The bounds of this factor are 1 and infinity, with a value of 1 describing a system for which only thermal neutrons are causing fissions. A value of 2 would denote a system in which thermal and fast neutrons are causing equal amounts of fissions.
- is the ratio of the number of neutrons that begin thermalization to the number of neutrons that reach thermal energies.
- Many isotopes have "resonances" in their capture cross-section curves that occur in energies between fast and thermal.
- If a neutron begins thermalization (i.e. begins to slow down), there is a possibility it will be absorbed by a non-multiplying material before it reaches thermal energy.
- The bounds of this factor are 0 and 1, with a value of 1 describing a system for which all fast neutrons that do not leak out and do not cause fast fissions eventually reach thermal energies.
- describes the probability that a thermal neutron will not escape the system without interacting.
- The bounds of this factor are 0 and 1, with a value of 1 describing a system for which thermal neutrons will never escape without interacting, i.e. an infinite system.
- Also written as
- is the ratio of number of thermal neutrons absorbed in by fissile nuclei versus the number of neutrons absorbed in all materials in the system.
- This factor describes the efficiency of thermal neutron utilization in the system, hence the name thermal utilization factor.
- The bounds of this factor are 0 and 1, with a value of 1 describing a system for which the entire system is made of fissile nuclei (i.e. thermal neutrons can only react with fissile materials). Similarly, a value of 0.5 describes a system for which reactions with fissile and non-fissile nuclei are equal.
- For a conventional nuclear power reactor, this factor is the only one that can be directly controlled by the operator. With manipulations to the control rods, you can increase the amount of neutrons being absorbed in non-fissile nuclei while simultaneously decreasing the amount of neutrons absorbed in fissile nuclei.
- describes the probability that a neutron absorbed will cause a fission reaction.
- This factor describes the behavior of the fissile material, specifically if a neutron is absorbed, how likely is it to cause a fission, and how many neutrons does the fission produce.
The multiplication factor is sometimes calculated with a simplified four-factor formula, which is the same as described above with and both equal to 1, and is used when an assumption is made that the reactor is "infinite" in that neutrons are very unlikely to leak out of the system. This value is often used in safety evaluations of reactor designs.
Criticality
Because the value of is directly related to the time rate of change of the neutron population in a system, it is convenient to classify the state of the nuclear system with regards to the critical value of the neutron population equation. The point at which the behavior of a nuclear system shifts is when is exactly equal to 1. This point is called "criticality," and describes a system in which the production rate and loss rate of neutrons is exactly equal.
When is less than or greater than one, the terms subcriticality and supercriticality are used respectively to describe the system:
- (subcriticality): The neutron population in the system is decreasing exponentially.
- (criticality): The neutron population is maintaining a constant value.
- (supercriticality): The neutron population in the system is increasing exponentially.
In a practical nuclear system, like a fission reactor, if criticality is intended it is likely that will actually oscillate from slightly less than 1 to slightly more than 1, primarily due to thermal feedback effects. The neutron population, when averaged over time, appears constant, leaving the average value of at around 1 during a constant power run. Both delayed neutrons and the transient fission product "burnable poisons" play an important role in the timing of these oscillations.
Reactivity
The value of is generally not easy to calculate or use practically. Instead, a system's reactivity is quantified instead. The reactivity of a nuclear system is qualitatively described as the departure from criticality. The equation below describes the pure reactivity as a function of the neutron multiplication factor :
or when comparing the reactivity differences between two nuclear systems with multiplication factors and ,
For most systems, the reactivity has a very small range, making any value difficult to qualitatively describe or interpret, like . Often, it is expressed in units of , per cent mille, or (almost solely in the United States) with the derived units of dollars and cents. Note that is often also expressed as
The value is known as the effective delayed neutron fraction, and it describes the fractional contribution of delayed neutrons to the fission rate of the system and is quantified as the ratio of the total number of fissions caused by delayed neutrons to the total number of fissions in a system. This number is slightly different than the delayed neutron fraction , which is the fraction of neutrons in the system that are delayed, because delayed neutrons are generally born at lower energies, and thus are easier to thermalize, meaning they are more likely to cause a fission than a prompt neutron. This weighting effect is given in the derivation of .
Subcritical Multiplication
When a nuclear system is subcritical, an introduction of neutrons to the system will result in that population decaying away; however, if neutrons are introduced at a constant rate (i.e. from a neutron source), a nuclear system can appear critical while not actually maintaining true criticality. This is called source criticality and due to a phenomenon called subcritical multiplication.
The neutron population equation can be modified to be written as follows:
This is a much more difficult differential equation to solve. In this case, we assume that all neutrons are from the source, and that each generation of neutrons is of equal magnitude. In this case, we can approximate using a geometric series:
We take the above equation and define a new factor , called the subcritical multiplication factor:
Multiplying this factor by the source strength (in neutrons/sec) will give the stable neutron population, as long as is known:
Much more commonly, this equation is used to estimate , as the stable neutron population is easy to measure, but it is difficult to know the strength of a neutron source. To get around this, as a system approaches criticality, approaches infinity; therefore, it is much more practical to measure , which approaches zero as a system approaches criticality. can be approximated by the ratio of count rates before and after a reactivity addition.
Most neutron sources are a combination of an alpha particle emitter and beryllium. Beryllium-9, the only naturally-occurring stable isotope of beryllium, is capable of emitting a neutron when an alpha particle is absorbed. This () binary reaction is what generates neutrons. The most common of these are americium-beryllium (AmBe), plutonium-beryllium (PuBe), and polonium-beryllium (PoBe) sources.
Antimony-124 is also used in conjunction with beryllium to generate neutrons, as the gamma ray emitted by antimony-124 is at a unique energy that can be absorbed by beryllium and cause it to emit a neutron. This is called a () reaction. Antimony-124 sources are commonly used to locate beryllium ore by mining companies.
Other sources of neutrons are from accelerators that use fusion to generate neutrons using deuterium and tritium fusion via this reaction
Special reactivity cases
Not all neutrons are emitted as a direct product of fission; some are instead due to the radioactive decay of some of the fission fragments. The neutrons that occur directly from fission are called "prompt neutrons", and the ones that are a result of radioactive decay of fission fragments are called "delayed neutrons". The fraction of neutrons that are delayed is called , as discussed before, and this fraction is typically less than 1% of all the neutrons in the chain reaction.
As the delayed neutron precursors (the radionuclides that decay via neutron emission) have decay constants on the order of seconds and milliseconds, the delayed neutrons born from them allow the neutron population in a system to respond to small reactivity changes several orders of magnitude more slowly than just prompt neutrons would alone, as these delayed neutrons effectively increase the mean neutron lifetime . Without delayed neutrons, changes in reaction rates in nuclear systems would occur at speeds that are too fast for humans to control.
When and , a nuclear system is called delayed critical. The region of supercriticality where is known as delayed supercriticality. It is in this region that all nuclear power reactors operate. When , the system is described as prompt critical. The region of supercriticality for is known as prompt supercriticality. This is the region in which nuclear weapons operate, alongside some pulsing nuclear research reactors, like the TRIGA reactor.

Nuclear weapons
See also: Nuclear weapon designNuclear fission weapons require a mass of fissile fuel that is prompt supercritical. For a given mass of fissile material the value of k can be increased by increasing the density. Since the probability per distance travelled for a neutron to collide with a nucleus is proportional to the material density, increasing the density of a fissile material can increase k. This concept is utilized in the implosion method for nuclear weapons. In these devices, the nuclear chain reaction begins after increasing the density of the fissile material with a conventional explosive.
In a gun-type fission weapon, two subcritical masses of fuel are rapidly brought together. The value of k for a combination of two masses is always greater than that of its components. The magnitude of the difference depends on distance, as well as the physical orientation. The value of k can also be increased by using a neutron reflector surrounding the fissile material.
Once the mass of fuel is prompt supercritical, the power increases exponentially. However, the exponential power increase cannot continue for long since k decreases when the amount of fission material that is left decreases (i.e. it is consumed by fissions). Also, the geometry and density are expected to change during detonation since the remaining fission material is torn apart from the explosion.
Predetonation

Detonation of a nuclear weapon involves bringing fissile material into its optimal supercritical state very rapidly (about one microsecond, or one-millionth of a second). During part of this process, the assembly is supercritical, but not yet in an optimal state for a chain reaction. Free neutrons, in particular from spontaneous fissions, can cause the device to undergo a preliminary chain reaction that destroys the fissile material before it is ready to produce a large explosion, which is known as predetonation.
To keep the probability of predetonation low, the duration of the non-optimal assembly period is minimized, and fissile and other materials are used that have low spontaneous fission rates. In fact, the combination of materials has to be such that it is unlikely that there is even a single spontaneous fission during the period of supercritical assembly. In particular, the gun method cannot be used with plutonium.
Nuclear power plants and control of chain reactions
Main articles: Chicago Pile-1, Nuclear reactor physics, and Nuclear criticality safetyChain reactions naturally give rise to reaction rates that grow (or shrink) exponentially, whereas a nuclear power reactor needs to be able to hold the reaction rate reasonably constant. To maintain this control, the chain reaction criticality must have a slow enough time scale to permit intervention by additional effects (e.g., mechanical control rods or thermal expansion). Consequently, all nuclear power reactors (even fast-neutron reactors) rely on delayed neutrons for their criticality. An operating nuclear power reactor fluctuates between being slightly subcritical and slightly delayed-supercritical, but must always remain below prompt-critical.
It is impossible for a nuclear power plant to undergo a nuclear chain reaction that results in an explosion of power comparable with a nuclear weapon, but even low-powered explosions from uncontrolled chain reactions (that would be considered "fizzles" in a bomb) may still cause considerable damage and meltdown in a reactor. For example, the Chernobyl disaster involved a runaway chain reaction, but the result was a low-powered steam explosion from the relatively small release of heat, as compared with a bomb. However, the reactor complex was destroyed by the heat, as well as by ordinary burning of the graphite exposed to air. Such steam explosions would be typical of the very diffuse assembly of materials in a nuclear reactor, even under the worst conditions.
In addition, other steps can be taken for safety. For example, power plants licensed in the United States require a negative void coefficient of reactivity (this means that if coolant is removed from the reactor core, the nuclear reaction will tend to shut down, not increase). This eliminates the possibility of the type of accident that occurred at Chernobyl (which was caused by a positive void coefficient). However, nuclear reactors are still capable of causing smaller chemical explosions even after complete shutdown, such as was the case of the Fukushima Daiichi nuclear disaster. In such cases, residual decay heat from the core may cause high temperatures if there is loss of coolant flow, even a day after the chain reaction has been shut down (see SCRAM). This may cause a chemical reaction between water and fuel that produces hydrogen gas, which can explode after mixing with air, with severe contamination consequences, since fuel rod material may still be exposed to the atmosphere from this process. However, such explosions do not happen during a chain reaction, but rather as a result of energy from radioactive beta decay, after the fission chain reaction has been stopped.
See also
References
- "See this 1956 Nobel lecture for history of the chain reaction in chemistry".
- Jogalekar, Ashutosh. "Leo Szil rd, a traffic light and a slice of nuclear history". Scientific American. Retrieved 4 January 2016.
- L. Szilárd, "Improvements in or relating to the transmutation of chemical elements," British patent number: GB630726 (filed: 28 June 1934; published: 30 March 1936). esp@cenet document view
- Lise Meitner: Otto Hahn - the discoverer of nuclear fission. In: Forscher und Wissenschaftler im heutigen Europa. Stalling Verlag, Oldenburg/Hamburg 1955.
- Lise Meitner & O. R. Frisch, "Disintegration of Uranium by Neutrons: A New Type of Nuclear Reaction," Nature 143, 3615 (1939-02-11): 239, Bibcode:1939Natur.143..239M, doi:10.1038/143239a0; O. R. Frisch, "Physical Evidence of Division of Heavy Nuclei under Neutron Bombardment," Nature 143, 3616 (1939-02-18): 276, doi:10.1038/143276a0. The paper is dated 16 January 1939. Meitner is identified as being at the Physical Institute, Academy of Sciences, Stockholm. Frisch is identified as being at the Institute of Theoretical Physics, University of Copenhagen.
- Hahn, O.; Strassmann, F. (February 1939). "Nachweis der Entstehung aktiver Bariumisotope aus Uran und Thorium durch Neutronenbestrahlung; Nachweis weiterer aktiver Bruchstücke bei der Uranspaltung". Naturwissenschaften. 27 (6): 89–95. Bibcode:1939NW.....27...89H. doi:10.1007/BF01488988. S2CID 33512939.
- H. von Halban, F. Joliot and L. Kowarski, Nature 143 (1939) 470 and 680.
- Bendjebbar, André (2000). Histoire secrète de la bombe atomique française (in French). Paris: Cherche Midi. ISBN 978-2-862-74794-1. OCLC 45842105.
- Anderson, H. L.; Fermi, E.; Szilárd, Leo (1 August 1939). "Neutron production and absorption in uranium" (PDF). Physical Review. 56 (3): 284–286. Bibcode:1939PhRv...56..284A. doi:10.1103/PhysRev.56.284.
- Lanouette, William; Silard, Bela (1992). Genius in the Shadows: A Biography of Leo Szilárd: The Man Behind The Bomb. New York: Charles Scribner's Sons. pp. 199, 202. ISBN 978-0-684-19011-2.
- Holl, Jack (1997). Argonne National Laboratory, 1946-96. University of Illinois Press. ISBN 978-0-252-02341-5.
- Oklo: Natural Nuclear Reactors—Fact Sheet Archived 2008-10-20 at the Wayback Machine
- "Nuclear Fuel Cycle Overview - World Nuclear Association". www.world-nuclear.org. Retrieved 2020-03-18.
- "Nuclear explained - U.S. Energy Information Administration (EIA)". www.eia.gov. Retrieved 2020-03-18.
- "Plutonium - World Nuclear Association". www.world-nuclear.org. Retrieved 2020-03-18.
- ^ Duderstadt, James; Hamilton, Louis (1976). Nuclear Reactor Analysis. John Wiley & Sons, Inc. ISBN 978-0-471-22363-4.
- ^ Lamarsh, John; Baratta, Anthony (2001). Introduction to Nuclear Engineering. Prentice Hall. ISBN 978-0-201-82498-8.
- Talamo, A.; Gohar, Y. (2010). Deterministic and Monte Carlo Analyses of YALINA Thermal Subcritical Assembly (Technical report). Argonne National Laboratory. doi:10.2172/991100. OSTI 991100.
- Carey Sublette (February 20, 1999). "4.1.5.3 Predetonation". 4. Engineering and Design of Nuclear Weapons: 4.1 Elements of Fission Weapon Design. Retrieved June 29, 2014.
External links
- Nuclear Chain Reaction Animation
- Annotated bibliography on nuclear chain reactions from the Alsos Digital Library
- Stochastic Java simulation of nuclear chain reaction Archived 2011-06-11 at the Wayback Machine by Wolfgang Bauer


 , is the average time between the emission of a neutron and either its absorption or escape from the system. The neutrons that occur directly from fission are called
, is the average time between the emission of a neutron and either its absorption or escape from the system. The neutrons that occur directly from fission are called 
 is most often quantified as the ratio of the rate of neutron production to the rate of neutron loss in a nuclear system, and it is often described using the
is most often quantified as the ratio of the rate of neutron production to the rate of neutron loss in a nuclear system, and it is often described using the 

 , this equation represents the neutron population
, this equation represents the neutron population  at any given time
at any given time  given an initial neutron population
given an initial neutron population  at
at  :
:


 is the reactor power at time
is the reactor power at time  , and
, and  , the
, the 
 , the fast fission factor
, the fast fission factor  , the resonance escape probability
, the resonance escape probability  , the probability of thermal non-leakage
, the probability of thermal non-leakage  , the thermal utilization factor
, the thermal utilization factor  , and the neutron reproduction factor
, and the neutron reproduction factor  (also called the neutron efficiency factor). The six-factor formula is traditionally written as follows:
(also called the neutron efficiency factor). The six-factor formula is traditionally written as follows:



 is often used in safety evaluations of reactor designs.
is often used in safety evaluations of reactor designs.
 (
( (
( (
( as a function of the neutron multiplication factor
as a function of the neutron multiplication factor 
 and
and  ,
,

 ,
, 



 is known as the effective delayed neutron fraction, and it describes the fractional contribution of delayed neutrons to the fission rate of the system and is quantified as the ratio of the total number of fissions caused by delayed neutrons to the total number of fissions in a system. This number is slightly different than the delayed neutron fraction
is known as the effective delayed neutron fraction, and it describes the fractional contribution of delayed neutrons to the fission rate of the system and is quantified as the ratio of the total number of fissions caused by delayed neutrons to the total number of fissions in a system. This number is slightly different than the delayed neutron fraction  , which is the fraction of neutrons in the system that are
, which is the fraction of neutrons in the system that are 

 , called the subcritical multiplication factor:
, called the subcritical multiplication factor:


 , which approaches zero as a system approaches criticality.
, which approaches zero as a system approaches criticality. 
 ) binary reaction is what generates neutrons. The most common of these are americium-beryllium (AmBe), plutonium-beryllium (PuBe), and polonium-beryllium (PoBe) sources.
) binary reaction is what generates neutrons. The most common of these are americium-beryllium (AmBe), plutonium-beryllium (PuBe), and polonium-beryllium (PoBe) sources.

 ) reaction. Antimony-124 sources are commonly used to locate beryllium ore by mining companies.
) reaction. Antimony-124 sources are commonly used to locate beryllium ore by mining companies.



 and
and  , a nuclear system is called
, a nuclear system is called  is known as delayed supercriticality. It is in this region that all nuclear power reactors operate. When
is known as delayed supercriticality. It is in this region that all nuclear power reactors operate. When  , the system is described as prompt critical. The region of supercriticality for
, the system is described as prompt critical. The region of supercriticality for  is known as prompt supercriticality. This is the region in which nuclear weapons operate, alongside some pulsing nuclear research reactors, like the
is known as prompt supercriticality. This is the region in which nuclear weapons operate, alongside some pulsing nuclear research reactors, like the