In general relativity, Regge–Wheeler–Zerilli equations are a pair of equations that describes gravitational perturbations of a Schwarzschild black hole, named after Tullio Regge, John Archibald Wheeler and Frank J. Zerilli. The perturbations of a Schwarzchild metric is classified into two types, namely, axial and polar perturbations, a terminology introduced by Subrahmanyan Chandrasekhar. Axial perturbations induce frame dragging by imparting rotations to the black hole and change sign when azimuthal direction is reversed, whereas polar perturbations do not impart rotations and do not change sign under the reversal of azimuthal direction. The equation for axial perturbations is called Regge–Wheeler equation and the equation governing polar perturbations is called Zerilli equation.
The equations take the same form as the one-dimensional Schrödinger equation. The equations read as
where characterizes the polar perturbations and the axial perturbations. Here is the tortoise coordinate (we set ), belongs to the Schwarzschild coordinates , is the Schwarzschild radius and represents the time frequency of the perturbations appearing in the form . The Regge–Wheeler potential and Zerilli potential are respectively given by
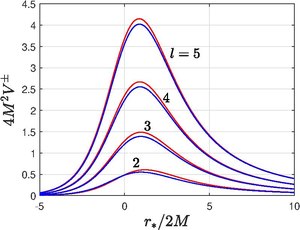
where and characterizes the eigenmode for the coordinate. For gravitational perturbations, the modes are irrelevant because they do not evolve with time. Physically gravitational perturbations with (monopole) mode represents a change in the black hole mass, whereas the (dipole) mode corresponds to a shift in the location and value of the black hole's angular momentum. The shape of above potentials are exhibited in the figure.
Remember that in the tortoise coordinate, denotes event horizon and is equivalent to i.e., to distances far away from the back hole. The potentials are short ranged as they decay faster than ; as we have and as , we have Consequently, the asymptotic behaviour of the solutions for is
Relations between the two problems
In 1975, Subrahmanyan Chandrasekhar and Steven Detweiler discovered a one-to-one mapping between the two equations, leading to a consequence that the spectrum corresponding to both potentials are identical. The two potentials can also be written as
The relations between and are given by
Reflection and transmission coefficients
Here is always positive and the problem is one of reflection and transmission of waves incident from to . The problem is essentially the same as that of a reflection and transmission problem by a potential barrier in quantum mechanics. Let the incident wave with unit amplitude be , then the asymptotic behaviours of the solution are given by
where and are respectively are the reflection and transmission amplitudes. In the second equation, we have imposed the physical requirement that no waves emerge from the event horizon.
The reflection and transmission coefficients are thus defined as
subjected to the condition Because of the inherent connection between the two equations as outlined in the previous section, it turns out
and thus consequently, since and differ only in their phases, we get
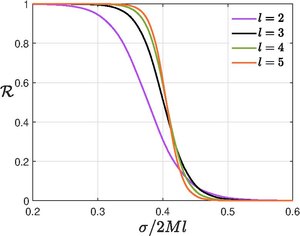
It is clear from the figure for the reflection coefficient that small-frequency perturbations are readily reflected by the black hole whereas large-frequency ones are absorbed by the black hole.
Quasi-normal modes
Quasi-normal modes correspond to pure tones of the black hole. It describes for arbitrary, but small, perturbations such as an object falling into the black hole, accretion of matter surrounding it, last stage of slightly aspherical collapse etc. Unlike the reflection and transmission coefficient problem, quasi-normal modes are characterised by complex-valued 's with the convention . The required boundary conditions are
indicating that we have purely outgoing waves with amplitude and purely ingoing waves at the horizon.
The problem becomes an eigenvalue problem. The quasi-normal modes are of damping type in time, although these waves diverge in space as (this is due to the implicit assumption that the perturbation in quasi-normal modes is 'infinite' in the remote past). Again because of the relation mentioned between the two problem, the spectrum of and are identical and thus it enough to consider the spectrum of The problem is simplified by introducing
The nonlinear eigenvalue problem is given by
The solution is found to exist only for a discrete set of values of This equation also implies the identity
See also
References
- Regge, T., & Wheeler, J. A. (1957). Stability of a Schwarzschild singularity. Physical Review, 108(4), 1063.
- Zerilli, F. J. (1970). Effective potential for even-parity Regge-Wheeler gravitational perturbation equations. Physical Review Letters, 24(13), 737.
- ^ Chandrasekhar, S.(1983). The mathematical theory of black holes. Oxford university press.
- ^ Chandrasekhar, S., & Detweiler, S. (1975). The quasi-normal modes of the Schwarzschild black hole. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 344(1639), 441-452.
- Nollert, H. P. (1993). Quasinormal modes of Schwarzschild black holes: The determination of quasinormal frequencies with very large imaginary parts. Physical Review D, 47(12), 5253.

 characterizes the polar perturbations and
characterizes the polar perturbations and  the axial perturbations. Here
the axial perturbations. Here  is the
is the  ),
),  belongs to the Schwarzschild coordinates
belongs to the Schwarzschild coordinates  ,
,  is the
is the  represents the time frequency of the perturbations appearing in the form
represents the time frequency of the perturbations appearing in the form  . The Regge–Wheeler potential and Zerilli potential are respectively given by
. The Regge–Wheeler potential and Zerilli potential are respectively given by


 and
and  characterizes the eigenmode for the
characterizes the eigenmode for the  coordinate. For gravitational perturbations, the modes
coordinate. For gravitational perturbations, the modes  are irrelevant because they do not evolve with time. Physically gravitational perturbations with
are irrelevant because they do not evolve with time. Physically gravitational perturbations with  (monopole) mode represents a change in the black hole mass, whereas the
(monopole) mode represents a change in the black hole mass, whereas the  (dipole) mode corresponds to a shift in the location and value of the black hole's angular momentum. The shape of above potentials are exhibited in the figure.
(dipole) mode corresponds to a shift in the location and value of the black hole's angular momentum. The shape of above potentials are exhibited in the figure.
 denotes
denotes  is equivalent to
is equivalent to  i.e., to distances far away from the back hole. The potentials are short ranged as they decay faster than
i.e., to distances far away from the back hole. The potentials are short ranged as they decay faster than  ; as
; as  and as
and as  Consequently, the asymptotic behaviour of the solutions for
Consequently, the asymptotic behaviour of the solutions for  is
is 


 is always positive and the problem is one of reflection and transmission of waves incident from
is always positive and the problem is one of reflection and transmission of waves incident from  , then the asymptotic behaviours of the solution are given by
, then the asymptotic behaviours of the solution are given by


 and
and  are respectively are the reflection and transmission amplitudes. In the second equation, we have imposed the physical requirement that no waves emerge from the event horizon.
are respectively are the reflection and transmission amplitudes. In the second equation, we have imposed the physical requirement that no waves emerge from the event horizon.

 Because of the inherent connection between the two equations as outlined in the previous section, it turns out
Because of the inherent connection between the two equations as outlined in the previous section, it turns out

 and
and  differ only in their phases, we get
differ only in their phases, we get

 . The required boundary conditions are
. The required boundary conditions are


 and purely ingoing waves at the horizon.
and purely ingoing waves at the horizon.
 (this is due to the implicit assumption that the perturbation in quasi-normal modes is 'infinite' in the remote past). Again because of the relation mentioned between the two problem, the spectrum of
(this is due to the implicit assumption that the perturbation in quasi-normal modes is 'infinite' in the remote past). Again because of the relation mentioned between the two problem, the spectrum of  The problem is simplified by introducing
The problem is simplified by introducing


 This equation also implies the identity
This equation also implies the identity
