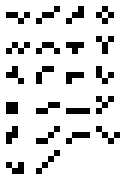
A pseudo-polyomino, also called a polyking, polyplet or hinged polyomino, is a plane geometric figure formed by joining one or more equal squares edge-to-edge or corner-to-corner at 90°. It is a polyform with square cells. The polyominoes are a subset of the polykings.
The name "polyking" refers to the king in chess. The n-kings are the n-square shapes which could be occupied by a king on an infinite chessboard in the course of legal moves.
Golomb uses the term pseudo-polyomino referring to kingwise-connected sets of squares.
Enumeration of polykings

Free, one-sided, and fixed polykings
There are three common ways of distinguishing polyominoes and polykings for enumeration:
- free polykings are distinct when none is a rigid transformation (translation, rotation, reflection or glide reflection) of another (pieces that can be picked up and flipped over).
- one-sided polykings are distinct when none is a translation or rotation of another (pieces that cannot be flipped over).
- fixed polykings are distinct when none is a translation of another (pieces that can be neither flipped nor rotated).
The following table shows the numbers of polykings of various types with n cells.
| n | free | one-sided | fixed |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 4 |
| 3 | 5 | 6 | 20 |
| 4 | 22 | 34 | 110 |
| 5 | 94 | 166 | 638 |
| 6 | 524 | 991 | 3832 |
| 7 | 3,031 | 5,931 | 23,592 |
| 8 | 18,770 | 37,196 | 147,941 |
| 9 | 118,133 | 235,456 | 940,982 |
| 10 | 758,381 | 1,514,618 | 6,053,180 |
| 11 | 4,915,652 | 9,826,177 | 39,299,408 |
| 12 | 32,149,296 | 64,284,947 | 257,105,146 |
| OEIS | A030222 | A030233 | A006770 |
Notes
- ^ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8.
External links
| Polyforms | |
|---|---|
| Polyominoes | |
| Higher dimensions | |
| Others | |
| Games and puzzles | |


