| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (February 2022) (Learn how and when to remove this message) |


In physics, interference is a phenomenon in which two coherent waves are combined by adding their intensities or displacements with due consideration for their phase difference. The resultant wave may have greater intensity (constructive interference) or lower amplitude (destructive interference) if the two waves are in phase or out of phase, respectively. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves as well as in loudspeakers as electrical waves.
Etymology
The word interference is derived from the Latin words inter which means "between" and fere which means "hit or strike", and was used in the context of wave superposition by Thomas Young in 1801.
Mechanisms
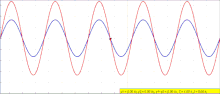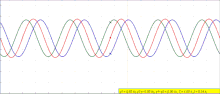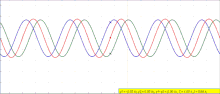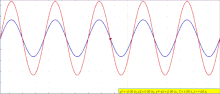

The principle of superposition of waves states that when two or more propagating waves of the same type are incident on the same point, the resultant amplitude at that point is equal to the vector sum of the amplitudes of the individual waves. If a crest of a wave meets a crest of another wave of the same frequency at the same point, then the amplitude is the sum of the individual amplitudes—this is constructive interference. If a crest of one wave meets a trough of another wave, then the amplitude is equal to the difference in the individual amplitudes—this is known as destructive interference. In ideal mediums (water, air are almost ideal) energy is always conserved, at points of destructive interference, the wave amplitudes cancel each other out, and the energy is redistributed to other areas. For example, when two pebbles are dropped in a pond, a pattern is observable; but eventually waves continue, and only when they reach the shore is the energy absorbed away from the medium.

Constructive interference occurs when the phase difference between the waves is an even multiple of π (180°), whereas destructive interference occurs when the difference is an odd multiple of π. If the difference between the phases is intermediate between these two extremes, then the magnitude of the displacement of the summed waves lies between the minimum and maximum values.
Consider, for example, what happens when two identical stones are dropped into a still pool of water at different locations. Each stone generates a circular wave propagating outwards from the point where the stone was dropped. When the two waves overlap, the net displacement at a particular point is the sum of the displacements of the individual waves. At some points, these will be in phase, and will produce a maximum displacement. In other places, the waves will be in anti-phase, and there will be no net displacement at these points. Thus, parts of the surface will be stationary—these are seen in the figure above and to the right as stationary blue-green lines radiating from the centre.
Interference of light is a unique phenomenon in that we can never observe superposition of the EM field directly as we can, for example, in water. Superposition in the EM field is an assumed phenomenon and necessary to explain how two light beams pass through each other and continue on their respective paths. Prime examples of light interference are the famous double-slit experiment, laser speckle, anti-reflective coatings and interferometers.
In addition to classical wave model for understanding optical interference, quantum matter waves also demonstrate interference.
Real-valued wave functions
The above can be demonstrated in one dimension by deriving the formula for the sum of two waves. The equation for the amplitude of a sinusoidal wave traveling to the right along the x-axis is where is the peak amplitude, is the wavenumber and is the angular frequency of the wave. Suppose a second wave of the same frequency and amplitude but with a different phase is also traveling to the right where is the phase difference between the waves in radians. The two waves will superpose and add: the sum of the two waves is Using the trigonometric identity for the sum of two cosines: this can be written This represents a wave at the original frequency, traveling to the right like its components, whose amplitude is proportional to the cosine of .
- Constructive interference: If the phase difference is an even multiple of π: then , so the sum of the two waves is a wave with twice the amplitude
- Destructive interference: If the phase difference is an odd multiple of π: then , so the sum of the two waves is zero
Between two plane waves


A simple form of interference pattern is obtained if two plane waves of the same frequency intersect at an angle. One wave is travelling horizontally, and the other is travelling downwards at an angle θ to the first wave. Assuming that the two waves are in phase at the point B, then the relative phase changes along the x-axis. The phase difference at the point A is given by
It can be seen that the two waves are in phase when
and are half a cycle out of phase when
Constructive interference occurs when the waves are in phase, and destructive interference when they are half a cycle out of phase. Thus, an interference fringe pattern is produced, where the separation of the maxima is
and df is known as the fringe spacing. The fringe spacing increases with increase in wavelength, and with decreasing angle θ.
The fringes are observed wherever the two waves overlap and the fringe spacing is uniform throughout.
Between two spherical waves

A point source produces a spherical wave. If the light from two point sources overlaps, the interference pattern maps out the way in which the phase difference between the two waves varies in space. This depends on the wavelength and on the separation of the point sources. The figure to the right shows interference between two spherical waves. The wavelength increases from top to bottom, and the distance between the sources increases from left to right.
When the plane of observation is far enough away, the fringe pattern will be a series of almost straight lines, since the waves will then be almost planar.
Multiple beams
Interference occurs when several waves are added together provided that the phase differences between them remain constant over the observation time.
It is sometimes desirable for several waves of the same frequency and amplitude to sum to zero (that is, interfere destructively, cancel). This is the principle behind, for example, 3-phase power and the diffraction grating. In both of these cases, the result is achieved by uniform spacing of the phases.
It is easy to see that a set of waves will cancel if they have the same amplitude and their phases are spaced equally in angle. Using phasors, each wave can be represented as for waves from to , where
To show that
one merely assumes the converse, then multiplies both sides by
The Fabry–Pérot interferometer uses interference between multiple reflections.
A diffraction grating can be considered to be a multiple-beam interferometer; since the peaks which it produces are generated by interference between the light transmitted by each of the elements in the grating; see interference vs. diffraction for further discussion.
Complex valued wave functions
Mechanical and gravity waves can be directly observed: they are real-valued wave functions; optical and matter waves cannot be directly observed: they are complex valued wave functions. Some of the differences between real valued and complex valued wave interference include:
- The interference involves different types of mathematical functions: A classical wave is a real function representing the displacement from an equilibrium position; an optical or quantum wavefunction is a complex function. A classical wave at any point can be positive or negative; the quantum probability function is non-negative.
- Any two different real waves in the same medium interfere; complex waves must be coherent to interfere. In practice this means the wave must come from the same source and have similar frequencies
- Real wave interference is obtained simply by adding the displacements from equilibrium (or amplitudes) of the two waves; In complex wave interference, we measure the modulus of the wavefunction squared.
Optical wave interference

Because the frequency of light waves (~10 Hz) is too high for currently available detectors to detect the variation of the electric field of the light, it is possible to observe only the intensity of an optical interference pattern. The intensity of the light at a given point is proportional to the square of the average amplitude of the wave. This can be expressed mathematically as follows. The displacement of the two waves at a point r is:
where A represents the magnitude of the displacement, φ represents the phase and ω represents the angular frequency.
The displacement of the summed waves is
The intensity of the light at r is given by
This can be expressed in terms of the intensities of the individual waves as
Thus, the interference pattern maps out the difference in phase between the two waves, with maxima occurring when the phase difference is a multiple of 2π. If the two beams are of equal intensity, the maxima are four times as bright as the individual beams, and the minima have zero intensity.
Classically the two waves must have the same polarization to give rise to interference fringes since it is not possible for waves of different polarizations to cancel one another out or add together. Instead, when waves of different polarization are added together, they give rise to a wave of a different polarization state.
Quantum mechanically the theories of Paul Dirac and Richard Feynman offer a more modern approach. Dirac showed that every quanta or photon of light acts on its own which he famously stated as "every photon interferes with itself". Richard Feynman showed that by evaluating a path integral where all possible paths are considered, that a number of higher probability paths will emerge. In thin films for example, film thickness which is not a multiple of light wavelength will not allow the quanta to traverse, only reflection is possible.
Light source requirements
The discussion above assumes that the waves which interfere with one another are monochromatic, i.e. have a single frequency—this requires that they are infinite in time. This is not, however, either practical or necessary. Two identical waves of finite duration whose frequency is fixed over that period will give rise to an interference pattern while they overlap. Two identical waves which consist of a narrow spectrum of frequency waves of finite duration (but shorter than their coherence time), will give a series of fringe patterns of slightly differing spacings, and provided the spread of spacings is significantly less than the average fringe spacing, a fringe pattern will again be observed during the time when the two waves overlap.
Conventional light sources emit waves of differing frequencies and at different times from different points in the source. If the light is split into two waves and then re-combined, each individual light wave may generate an interference pattern with its other half, but the individual fringe patterns generated will have different phases and spacings, and normally no overall fringe pattern will be observable. However, single-element light sources, such as sodium- or mercury-vapor lamps have emission lines with quite narrow frequency spectra. When these are spatially and colour filtered, and then split into two waves, they can be superimposed to generate interference fringes. All interferometry prior to the invention of the laser was done using such sources and had a wide range of successful applications.
A laser beam generally approximates much more closely to a monochromatic source, and thus it is much more straightforward to generate interference fringes using a laser. The ease with which interference fringes can be observed with a laser beam can sometimes cause problems in that stray reflections may give spurious interference fringes which can result in errors.
Normally, a single laser beam is used in interferometry, though interference has been observed using two independent lasers whose frequencies were sufficiently matched to satisfy the phase requirements. This has also been observed for widefield interference between two incoherent laser sources.
It is also possible to observe interference fringes using white light. A white light fringe pattern can be considered to be made up of a 'spectrum' of fringe patterns each of slightly different spacing. If all the fringe patterns are in phase in the centre, then the fringes will increase in size as the wavelength decreases and the summed intensity will show three to four fringes of varying colour. Young describes this very elegantly in his discussion of two slit interference. Since white light fringes are obtained only when the two waves have travelled equal distances from the light source, they can be very useful in interferometry, as they allow the zero path difference fringe to be identified.
Optical arrangements
To generate interference fringes, light from the source has to be divided into two waves which then have to be re-combined. Traditionally, interferometers have been classified as either amplitude-division or wavefront-division systems.
In an amplitude-division system, a beam splitter is used to divide the light into two beams travelling in different directions, which are then superimposed to produce the interference pattern. The Michelson interferometer and the Mach–Zehnder interferometer are examples of amplitude-division systems.
In wavefront-division systems, the wave is divided in space—examples are Young's double slit interferometer and Lloyd's mirror.
Interference can also be seen in everyday phenomena such as iridescence and structural coloration. For example, the colours seen in a soap bubble arise from interference of light reflecting off the front and back surfaces of the thin soap film. Depending on the thickness of the film, different colours interfere constructively and destructively.
- Iridiscence caused by thin-film interference
-
 Smartphone with iridescent back panel
Smartphone with iridescent back panel
-
 An oil spill
An oil spill
-
 White light interference in a soap bubble.
White light interference in a soap bubble.
Quantum interference
See also: Double-slit experiment and Matter wave| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
Quantum interference – the observed wave-behavior of matter – resembles optical interference. Let be a wavefunction solution of the Schrödinger equation for a quantum mechanical object. Then the probability of observing the object at position is where * indicates complex conjugation. Quantum interference concerns the issue of this probability when the wavefunction is expressed as a sum or linear superposition of two terms :
Usually, and correspond to distinct situations A and B. When this is the case, the equation indicates that the object can be in situation A or situation B. The above equation can then be interpreted as: The probability of finding the object at is the probability of finding the object at when it is in situation A plus the probability of finding the object at when it is in situation B plus an extra term. This extra term, which is called the quantum interference term, is in the above equation. As in the classical wave case above, the quantum interference term can add (constructive interference) or subtract (destructive interference) from in the above equation depending on whether the quantum interference term is positive or negative. If this term is absent for all , then there is no quantum mechanical interference associated with situations A and B.
The best known example of quantum interference is the double-slit experiment. In this experiment, matter waves from electrons, atoms or molecules approach a barrier with two slits in it. One slit becomes and the other becomes . The interference pattern occurs on the far side, observed by detectors suitable to the particles originating the matter wave. The pattern matches the optical double slit pattern.
Applications
Beat
Main article: Beat (acoustics)In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, perceived as a periodic variation in volume whose rate is the difference of the two frequencies.
With tuning instruments that can produce sustained tones, beats can be readily recognized. Tuning two tones to a unison will present a peculiar effect: when the two tones are close in pitch but not identical, the difference in frequency generates the beating. The volume varies like in a tremolo as the sounds alternately interfere constructively and destructively. As the two tones gradually approach unison, the beating slows down and may become so slow as to be imperceptible. As the two tones get further apart, their beat frequency starts to approach the range of human pitch perception, the beating starts to sound like a note, and a combination tone is produced. This combination tone can also be referred to as a missing fundamental, as the beat frequency of any two tones is equivalent to the frequency of their implied fundamental frequency.
Interferometry
Main article: InterferometryInterferometry has played an important role in the advancement of physics, and also has a wide range of applications in physical and engineering measurement. The impact on physics and the applications span various types of waves.
Optical interferometry
Main article: Optical interferometryThomas Young's double slit interferometer in 1803 demonstrated interference fringes when two small holes were illuminated by light from another small hole which was illuminated by sunlight. Young was able to estimate the wavelength of different colours in the spectrum from the spacing of the fringes. The experiment played a major role in the general acceptance of the wave theory of light. In quantum mechanics, this experiment is considered to demonstrate the inseparability of the wave and particle natures of light and other quantum particles (wave–particle duality). Richard Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment.
The results of the Michelson–Morley experiment are generally considered to be the first strong evidence against the theory of a luminiferous aether and in favor of special relativity.
Interferometry has been used in defining and calibrating length standards. When the metre was defined as the distance between two marks on a platinum-iridium bar, Michelson and Benoît used interferometry to measure the wavelength of the red cadmium line in the new standard, and also showed that it could be used as a length standard. Sixty years later, in 1960, the metre in the new SI system was defined to be equal to 1,650,763.73 wavelengths of the orange-red emission line in the electromagnetic spectrum of the krypton-86 atom in a vacuum. This definition was replaced in 1983 by defining the metre as the distance travelled by light in vacuum during a specific time interval. Interferometry is still fundamental in establishing the calibration chain in length measurement.
Interferometry is used in the calibration of slip gauges (called gauge blocks in the US) and in coordinate-measuring machines. It is also used in the testing of optical components.
Radio interferometry
Main article: Astronomical interferometer
In 1946, a technique called astronomical interferometry was developed. Astronomical radio interferometers usually consist either of arrays of parabolic dishes or two-dimensional arrays of omni-directional antennas. All of the telescopes in the array are widely separated and are usually connected together using coaxial cable, waveguide, optical fiber, or other type of transmission line. Interferometry increases the total signal collected, but its primary purpose is to vastly increase the resolution through a process called Aperture synthesis. This technique works by superposing (interfering) the signal waves from the different telescopes on the principle that waves that coincide with the same phase will add to each other while two waves that have opposite phases will cancel each other out. This creates a combined telescope that is equivalent in resolution (though not in sensitivity) to a single antenna whose diameter is equal to the spacing of the antennas farthest apart in the array.
Acoustic interferometry
An acoustic interferometer is an instrument for measuring the physical characteristics of sound waves in a gas or liquid, such velocity, wavelength, absorption, or impedance. A vibrating crystal creates ultrasonic waves that are radiated into the medium. The waves strike a reflector placed parallel to the crystal, reflected back to the source and measured.
See also
- Active noise control
- Beat (acoustics)
- Coherence (physics)
- Diffraction
- Haidinger fringes
- Interference lithography
- Interference visibility
- Interferometer
- Lloyd's Mirror
- Moiré pattern
- Multipath interference
- Newton's rings
- Optical path length
- Thin-film interference
- Rayleigh roughness criterion
- Upfade
References
- On the mechanism of the eye / by Thomas Young.; Young, Thomas; University College, London Library Services (1801). Young, Thomas, 1773-1829. University College London (UCL) UCL Library Services. London : printed by W. Bulmer and Co., Cleveland Row, St. James's.
- Jones, Peter Ward (2001). Oxford University Press. Oxford Music Online. Oxford University Press. doi:10.1093/gmo/9781561592630.article.20622.
- Kipnis, Nahum (1991). History of the Principle of Interference of Light. doi:10.1007/978-3-0348-8652-9. ISBN 978-3-0348-9717-4.
- Ockenga, Wymke. Phase contrast. Leika Science Lab, 09 June 2011. "If two waves interfere, the amplitude of the resulting light wave will be equal to the vector sum of the amplitudes of the two interfering waves."
- Steel, W. H. (1986). Interferometry. Cambridge: Cambridge University Press. ISBN 0-521-31162-4.
- Pfleegor, R. L.; Mandel, L. (1967). "Interference of independent photon beams". Phys. Rev. 159 (5): 1084–1088. Bibcode:1967PhRv..159.1084P. doi:10.1103/physrev.159.1084.
- Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2014). "Widefield two laser interferometry". Optics Express. 22 (22): 27094–27101. Bibcode:2014OExpr..2227094P. doi:10.1364/OE.22.027094. PMID 25401860.
- ^ Born, Max; Wolf, Emil (1999). Principles of Optics. Cambridge: Cambridge University Press. ISBN 0-521-64222-1.
- Feynman R, Leighton R, and Sands M., The Feynman Lectures Website, September 2013."The Feynman Lectures on Physics, Volume III" (online edition)
- Bach, Roger; Pope, Damian; Liou, Sy-Hwang; Batelaan, Herman (2013-03-13). "Controlled double-slit electron diffraction". New Journal of Physics. 15 (3). IOP Publishing: 033018. arXiv:1210.6243. doi:10.1088/1367-2630/15/3/033018. ISSN 1367-2630. S2CID 832961.
- Levitin, Daniel J. (2006). This is Your Brain on Music: The Science of a Human Obsession. Dutton. p. 22. ISBN 978-0525949695.
- Greene, Brian (1999). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton. pp. 97–109. ISBN 978-0-393-04688-5.
- RS Longhurst, Geometrical and Physical Optics, 1968, Longmans, London.
External links
- Easy JavaScript Simulation Model of One Dimensional Wave Interference
- Expressions of position and fringe spacing
- Java simulation of interference of water waves 1
- Java simulation of interference of water waves 2
- Flash animations demonstrating interference Archived 2009-06-24 at the Wayback Machine
 where
where  is the peak amplitude,
is the peak amplitude,  is the
is the  is the
is the  where
where  is the phase difference between the waves in
is the phase difference between the waves in  Using the
Using the  this can be written
this can be written
 This represents a wave at the original frequency, traveling to the right like its components, whose amplitude is proportional to the cosine of
This represents a wave at the original frequency, traveling to the right like its components, whose amplitude is proportional to the cosine of  .
.
 then
then  , so the sum of the two waves is a wave with twice the amplitude
, so the sum of the two waves is a wave with twice the amplitude 
 then
then  , so the sum of the two waves is zero
, so the sum of the two waves is zero 




 for
for  waves from
waves from  to
to  , where
, where









 be a
be a  of observing the object at position
of observing the object at position  is
is  where * indicates
where * indicates  :
:

 and
and  correspond to distinct situations A and B. When this is the case, the equation
correspond to distinct situations A and B. When this is the case, the equation  in the above equation. As in the
in the above equation. As in the  in the above equation depending on whether the quantum interference term is positive or negative. If this term is absent for all
in the above equation depending on whether the quantum interference term is positive or negative. If this term is absent for all