In thermodynamics, the Joule–Thomson effect (also known as the Joule–Kelvin effect or Kelvin–Joule effect) describes the temperature change of a real gas or liquid (as differentiated from an ideal gas) when it is expanding; typically caused by the pressure loss from flow through a valve or porous plug while keeping it insulated so that no heat is exchanged with the environment. This procedure is called a throttling process or Joule–Thomson process. The effect is purely an effect due to deviation from ideality, as any ideal gas has no JT effect.
At room temperature, all gases except hydrogen, helium, and neon cool upon expansion by the Joule–Thomson process when being throttled through an orifice; these three gases rise in temperature when forced through a porous plug at room temperature, but lowers in temperature when already at lower temperatures. Most liquids such as hydraulic oils will be warmed by the Joule–Thomson throttling process. The temperature at which the JT effect switches sign is the inversion temperature.
The gas-cooling throttling process is commonly exploited in refrigeration processes such as liquefiers in air separation industrial process. In hydraulics, the warming effect from Joule–Thomson throttling can be used to find internally leaking valves as these will produce heat which can be detected by thermocouple or thermal-imaging camera. Throttling is a fundamentally irreversible process. The throttling due to the flow resistance in supply lines, heat exchangers, regenerators, and other components of (thermal) machines is a source of losses that limits their performance.
Since it is a constant-enthalpy process, it can be used to experimentally measure the lines of constant enthalpy (isenthalps) on the diagram of a gas. Combined with the specific heat capacity at constant pressure it allows the complete measurement of the thermodynamic potential for the gas.
History
The effect is named after James Prescott Joule and William Thomson, 1st Baron Kelvin, who discovered it in 1852. It followed upon earlier work by Joule on Joule expansion, in which a gas undergoes free expansion in a vacuum and the temperature is unchanged, if the gas is ideal.
Description
The adiabatic (no heat exchanged) expansion of a gas may be carried out in a number of ways. The change in temperature experienced by the gas during expansion depends not only on the initial and final pressure, but also on the manner in which the expansion is carried out.
- If the expansion process is reversible, meaning that the gas is in thermodynamic equilibrium at all times, it is called an isentropic expansion. In this scenario, the gas does positive work during the expansion, and its temperature decreases.
- In a free expansion, on the other hand, the gas does no work and absorbs no heat, so the internal energy is conserved. Expanded in this manner, the temperature of an ideal gas would remain constant, but the temperature of a real gas decreases, except at very high temperature.
- The method of expansion discussed in this article, in which a gas or liquid at pressure P1 flows into a region of lower pressure P2 without significant change in kinetic energy, is called the Joule–Thomson expansion. The expansion is inherently irreversible. During this expansion, enthalpy remains unchanged (see proof below). Unlike a free expansion, work is done, causing a change in internal energy. Whether the internal energy increases or decreases is determined by whether work is done on or by the fluid; that is determined by the initial and final states of the expansion and the properties of the fluid.
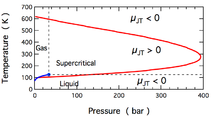
The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N2, are shown in the figure. Note that most conditions in the figure correspond to N2 being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N2) occurs as zero pressure is approached. For N2 gas at low pressures, is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N2 condenses to form a liquid and the coefficient again becomes negative. Thus, for N2 gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N2 forms.
Physical mechanism
There are two factors that can change the temperature of a fluid during an adiabatic expansion: a change in internal energy or the conversion between potential and kinetic internal energy. Temperature is the measure of thermal kinetic energy (energy associated with molecular motion); so a change in temperature indicates a change in thermal kinetic energy. The internal energy is the sum of thermal kinetic energy and thermal potential energy. Thus, even if the internal energy does not change, the temperature can change due to conversion between kinetic and potential energy; this is what happens in a free expansion and typically produces a decrease in temperature as the fluid expands. If work is done on or by the fluid as it expands, then the total internal energy changes. This is what happens in a Joule–Thomson expansion and can produce larger heating or cooling than observed in a free expansion.
In a Joule–Thomson expansion the enthalpy remains constant. The enthalpy, , is defined as
where is internal energy, is pressure, and is volume. Under the conditions of a Joule–Thomson expansion, the change in represents the work done by the fluid (see the proof below). If increases, with constant, then must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule–Thomson coefficient. Conversely, a decrease in means that work is done on the fluid and the internal energy increases. If the increase in kinetic energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative.
For an ideal gas, does not change during a Joule–Thomson expansion. As a result, there is no change in internal energy; since there is also no change in thermal potential energy, there can be no change in thermal kinetic energy and, therefore, no change in temperature. In real gases, does change.
The ratio of the value of to that expected for an ideal gas at the same temperature is called the compressibility factor, . For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in compressibility factor). At low pressure, the value of always moves towards unity as a gas expands. Thus at low temperature, and will increase as the gas expands, resulting in a positive Joule–Thomson coefficient. At high temperature, and decrease as the gas expands; if the decrease is large enough, the Joule–Thomson coefficient will be negative.
For liquids, and for supercritical fluids under high pressure, increases as pressure increases. This is due to molecules being forced together, so that the volume can barely decrease due to higher pressure. Under such conditions, the Joule–Thomson coefficient is negative, as seen in the figure above.
The physical mechanism associated with the Joule–Thomson effect is closely related to that of a shock wave, although a shock wave differs in that the change in bulk kinetic energy of the gas flow is not negligible.
The Joule–Thomson (Kelvin) coefficient
The rate of change of temperature with respect to pressure in a Joule–Thomson process (that is, at constant enthalpy ) is the Joule–Thomson (Kelvin) coefficient . This coefficient can be expressed in terms of the gas's specific volume , its heat capacity at constant pressure , and its coefficient of thermal expansion as:
See the § Derivation of the Joule–Thomson coefficient below for the proof of this relation. The value of is typically expressed in °C/bar (SI units: K/Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.
All real gases have an inversion point at which the value of changes sign. The temperature of this point, the Joule–Thomson inversion temperature, depends on the pressure of the gas before expansion.
In a gas expansion the pressure decreases, so the sign of is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
| If the gas temperature is | then is | since is | thus must be | so the gas |
|---|---|---|---|---|
| below the inversion temperature | positive | always negative | negative | cools |
| above the inversion temperature | negative | positive | warms |
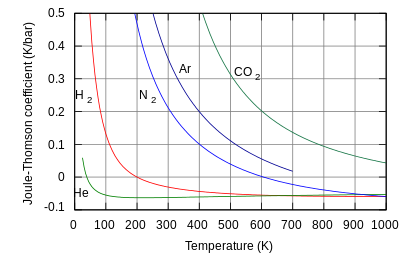
Helium and hydrogen are two gases whose Joule–Thomson inversion temperatures at a pressure of one atmosphere are very low (e.g., about 40 K, −233 °C for helium). Thus, helium and hydrogen warm when expanded at constant enthalpy at typical room temperatures. On the other hand, nitrogen and oxygen, the two most abundant gases in air, have inversion temperatures of 621 K (348 °C) and 764 K (491 °C) respectively: these gases can be cooled from room temperature by the Joule–Thomson effect.
For an ideal gas, is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.
Theoretical models

For a Van der Waals gas, the coefficient iswith inversion temperature .
For the Dieterici gas, the reduced inversion temperature is , and the relation between reduced pressure and reduced inversion temperature is . This is plotted on the right. The critical point falls inside the region where the gas cools on expansion. The outside region is where the gas warms on expansion.
Applications
In practice, the Joule–Thomson effect is achieved by allowing the gas to expand through a throttling device (usually a valve) which must be very well insulated to prevent any heat transfer to or from the gas. No external work is extracted from the gas during the expansion (the gas must not be expanded through a turbine, for example).
The cooling produced in the Joule–Thomson expansion makes it a valuable tool in refrigeration. The effect is applied in the Linde technique as a standard process in the petrochemical industry, where the cooling effect is used to liquefy gases, and in many cryogenic applications (e.g. for the production of liquid oxygen, nitrogen, and argon). A gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers, starting from ambient temperature, cannot be used to liquefy helium, hydrogen, or neon. They must first be cooled to their inversion temperatures, which are -233 C (helium), -71 C (hydrogen), and -42 C (neon).
Proof that the specific enthalpy remains constant
In thermodynamics so-called "specific" quantities are quantities per unit mass (kg) and are denoted by lower-case characters. So h, u, and v are the specific enthalpy, specific internal energy, and specific volume (volume per unit mass, or reciprocal density), respectively. In a Joule–Thomson process the specific enthalpy h remains constant. To prove this, the first step is to compute the net work done when a mass m of the gas moves through the plug. This amount of gas has a volume of V1 = m v1 in the region at pressure P1 (region 1) and a volume V2 = m v2 when in the region at pressure P2 (region 2). Then in region 1, the "flow work" done on the amount of gas by the rest of the gas is: W1 = m P1v1. In region 2, the work done by the amount of gas on the rest of the gas is: W2 = m P2v2. So, the total work done on the mass m of gas is
The change in internal energy minus the total work done on the amount of gas is, by the first law of thermodynamics, the total heat supplied to the amount of gas.
In the Joule–Thomson process, the gas is insulated, so no heat is absorbed. This means that
where u1 and u2 denote the specific internal energies of the gas in regions 1 and 2, respectively. Using the definition of the specific enthalpy h = u + Pv, the above equation implies that
where h1 and h2 denote the specific enthalpies of the amount of gas in regions 1 and 2, respectively.
Throttling in the T-s diagram

A convenient way to get a quantitative understanding of the throttling process is by using diagrams such as h-T diagrams, h-P diagrams, and others. Commonly used are the so-called T-s diagrams. Figure 2 shows the T-s diagram of nitrogen as an example. Various points are indicated as follows:
- T = 300 K, p = 200 bar, s = 5.16 kJ/(kgK), h = 430 kJ/kg;
- T = 270 K, p = 1 bar, s = 6.79 kJ/(kgK), h = 430 kJ/kg;
- T = 133 K, p = 200 bar, s = 3.75 kJ/(kgK), h = 150 kJ/kg;
- T = 77.2 K, p = 1 bar, s = 4.40 kJ/(kgK), h = 150 kJ/kg;
- T = 77.2 K, p = 1 bar, s = 2.83 kJ/(kgK), h = 28 kJ/kg (saturated liquid at 1 bar);
- T = 77.2 K, p = 1 bar, s = 5.41 kJ/(kgK), h = 230 kJ/kg (saturated gas at 1 bar).
As shown before, throttling keeps h constant. E.g. throttling from 200 bar and 300 K (point a in fig. 2) follows the isenthalpic (line of constant specific enthalpy) of 430 kJ/kg. At 1 bar it results in point b which has a temperature of 270 K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133 K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2 K. Since the enthalpy is an extensive parameter the enthalpy in d (hd) is equal to the enthalpy in e (he) multiplied with the mass fraction of the liquid in d (xd) plus the enthalpy in f (hf) multiplied with the mass fraction of the gas in d (1 − xd). So
With numbers: 150 = xd 28 + (1 − xd) 230 so xd is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.
Derivation of the Joule–Thomson coefficient
It is difficult to think physically about what the Joule–Thomson coefficient, , represents. Also, modern determinations of do not use the original method used by Joule and Thomson, but instead measure a different, closely related quantity. Thus, it is useful to derive relationships between and other, more conveniently measured quantities, as described below.
The first step in obtaining these results is to note that the Joule–Thomson coefficient involves the three variables T, P, and H. A useful result is immediately obtained by applying the cyclic rule; in terms of these three variables that rule may be written
Each of the three partial derivatives in this expression has a specific meaning. The first is , the second is the constant pressure heat capacity, , defined by
and the third is the inverse of the isothermal Joule–Thomson coefficient, , defined by
- .
This last quantity is more easily measured than . Thus, the expression from the cyclic rule becomes
This equation can be used to obtain Joule–Thomson coefficients from the more easily measured isothermal Joule–Thomson coefficient. It is used in the following to obtain a mathematical expression for the Joule–Thomson coefficient in terms of the volumetric properties of a fluid.
To proceed further, the starting point is the fundamental equation of thermodynamics in terms of enthalpy; this is
Now "dividing through" by dP, while holding temperature constant, yields
The partial derivative on the left is the isothermal Joule–Thomson coefficient, , and the one on the right can be expressed in terms of the coefficient of thermal expansion via a Maxwell relation. The appropriate relation is
where α is the cubic coefficient of thermal expansion. Replacing these two partial derivatives yields
This expression can now replace in the earlier equation for to obtain:
This provides an expression for the Joule–Thomson coefficient in terms of the commonly available properties heat capacity, molar volume, and thermal expansion coefficient. It shows that the Joule–Thomson inversion temperature, at which is zero, occurs when the coefficient of thermal expansion is equal to the inverse of the temperature. Since this is true at all temperatures for ideal gases (see expansion in gases), the Joule–Thomson coefficient of an ideal gas is zero at all temperatures.
Joule's second law
See also: Joule's first lawIt is easy to verify that for an ideal gas defined by suitable microscopic postulates that αT = 1, so the temperature change of such an ideal gas at a Joule–Thomson expansion is zero. For such an ideal gas, this theoretical result implies that:
- The internal energy of a fixed mass of an ideal gas depends only on its temperature (not pressure or volume).
This rule was originally found by Joule experimentally for real gases and is known as Joule's second law. More refined experiments found important deviations from it.
See also
- Critical point (thermodynamics)
- Enthalpy and Isenthalpic process
- Ideal gas
- Liquefaction of gases
- MIRI (Mid-Infrared Instrument), a J–T loop is used on one of the instruments of the James Webb Space Telescope
- Refrigeration
- Reversible process (thermodynamics)
References
- ^ R. H. Perry and D. W. Green (1984). Perry's Chemical Engineers' Handbook. McGraw-Hill. ISBN 978-0-07-049479-4.
- B. N. Roy (2002). Fundamentals of Classical and Statistical Thermodynamics. John Wiley & Sons. Bibcode:2002fcst.book.....N. ISBN 978-0-470-84313-0.
- ^ W. C. Edmister, B. I. Lee (1984). Applied Hydrocarbon Thermodynamics. Vol. 1 (2nd ed.). Gulf Publishing. ISBN 978-0-87201-855-6.
- F. Reif (1965). "Chapter 5 – Simple applications of macroscopic thermodynamics". Fundamentals of Statistical and Thermal Physics. McGraw-Hill. ISBN 978-0-07-051800-1.
- A. W. Adamson (1973). "Chapter 4 – Chemical thermodynamics. The First Law of Thermodynamics". A Textbook of Physical Chemistry (1st ed.). Academic Press. LCCN 72088328.
- G. W. Castellan (1971). "Chapter 7 – Energy and the First Law of Thermodynamics; Thermochemistry". Physical Chemistry (2nd ed.). Addison-Wesley. ISBN 978-0-201-00912-5.
- Moran, M.J.; Shapiro, H.N. (2006). Fundamentals of Engineering Thermodynamics (5th ed.). John Wiley & Sons.
- ^ De Waele, A. T. A. M. (2017). "Basics of Joule–Thomson Liquefaction and JT Cooling". Journal of Low Temperature Physics. 186 (5–6): 385–403. Bibcode:2017JLTP..186..385D. doi:10.1007/s10909-016-1733-3.
- ^ Pippard, Alfred B. (1981). Elements of classical thermodynamics: for advanced students of physics (Repr ed.). Cambridge: Univ. Pr. pp. 74–77. ISBN 978-0-521-09101-5.
- Goussard, Jacques-Olivier; Roulet, Bernard (1993). "Free expansion for real gases". American Journal of Physics. 61 (9): 845–848. Bibcode:1993AmJPh..61..845G. doi:10.1119/1.17417.
- ^ Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. p. 930. ISBN 978-0-7167-2871-9.
- Rock, P. A. (1983). Chemical Thermodynamics. Mill Valley, CA: University Science Books. sec. 3-2. ISBN 978-0-935702-12-5.
- Pippard, A. B. (1957). "Elements of Classical Thermodynamics", p. 73. Cambridge University Press, Cambridge, U.K.
- Tabor, D. (1991). Gases, liquids and solids, p. 148. Cambridge University Press, Cambridge, U.K. ISBN 0 521 40667 6.
- Klotz, I.M. and R. M. Rosenberg (1991). Chemical Thermodynamics, p. 83. Benjamin, Meno Park, California.
- ^ Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. pp. 31–32. ISBN 0-7167-2871-0.
- Hoover, Wm. G.; Hoover, Carol G.; Travis, Karl P. (2014). "Shock-Wave Compression and Joule–Thomson Expansion". Physical Review Letters. 112 (14): 144504. arXiv:1311.1717. Bibcode:2014PhRvL.112n4504H. doi:10.1103/PhysRevLett.112.144504. PMID 24765974. S2CID 33580985.
- W.R. Salzman. "Joule Expansion". Department of Chemistry, University of Arizona. Archived from the original on 13 June 2012. Retrieved 23 July 2005.
- "10.3: The Joule-Thomson Experiment". Physics LibreTexts. 25 January 2017. Retrieved 5 July 2023.
- Keenan, J.H. (1970). Thermodynamics, Chapter 15. M.I.T. Press, Cambridge, Massachusetts.
- See e.g. M.J. Moran and H.N. Shapiro "Fundamentals of Engineering Thermodynamics" 5th Edition (2006) John Wiley & Sons, Inc. page 147
- Figure composed with data obtained with REFPROP, NIST Standard Reference Database 23
- Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. pp. 89–90. ISBN 978-0-7167-2871-9.
- Keyes, F.G.; Collins, S.C. (1932). "The pressure variation of the heat function as a direct measure of the van der Waals forces". Proc. Natl. Acad. Sci. U.S.A. 18 (4): 328–333. Bibcode:1932PNAS...18..328K. doi:10.1073/pnas.18.4.328. PMC 1076221. PMID 16587688.
- Cusco, L.; McBain, S.E.; Saville, G. (1995). "A flow calorimeter for the measurement of the isothermal Joule–Thomson coefficient of gases at elevated temperatures and pressures. Results for nitrogen at temperatures up to 473 K and pressures up to 10 MPa and for carbon dioxide at temperatures up to 500 K and pressures up to 5 MPa". The Journal of Chemical Thermodynamics. 27 (7): 721–733. doi:10.1006/jcht.1995.0073.
- Callen, H.B (1960). Thermodynamics. New York: John Wiley and Sons. pp. 112–114.
- Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry, volume 1 Fundamental Principles. The Properties of Gases, Longmans, Green and Co., London, pp. 614–615.
- Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (1st edition 1968), third edition 1983, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0, p. 116.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 81.
Bibliography
- M. W. Zemansky (1968). Heat and Thermodynamics; An Intermediate Textbook. McGraw-Hill. pp. 182, 355. LCCN 67026891.
- D. V. Schroeder (2000). An Introduction to Thermal Physics. Addison Wesley Longman. p. 142. ISBN 978-0-201-38027-9.
- C. Kittel, H. Kroemer (1980). Thermal Physics. W. H. Freeman. ISBN 978-0-7167-1088-2.
External links
- Weisstein, Eric Wolfgang (ed.). "Joule-Thomson process". ScienceWorld.
- Weisstein, Eric Wolfgang (ed.). "Joule-Thomson coefficient". ScienceWorld.
- "Inversion Curve of Joule-Thomson Effect using Peng-Robinson CEOS". Demonstrations Projects of Wolfram Mathematica.
- Joule–Thomson effect module, University of Notre Dame
 diagram of a gas. Combined with the
diagram of a gas. Combined with the  it allows the complete measurement of the
it allows the complete measurement of the  for N2. Within the region bounded by the red line, a Joule–Thomson expansion produces cooling (
for N2. Within the region bounded by the red line, a Joule–Thomson expansion produces cooling ( ); outside that region, the expansion produces heating. The gas–liquid coexistence curve is shown by the blue line, terminating at the critical point (the solid blue circle). The dashed lines demarcate the region where N2 is a supercritical fluid (where properties smoothly transition between liquid-like and gas-like).
); outside that region, the expansion produces heating. The gas–liquid coexistence curve is shown by the blue line, terminating at the critical point (the solid blue circle). The dashed lines demarcate the region where N2 is a supercritical fluid (where properties smoothly transition between liquid-like and gas-like). , is defined as
, is defined as

 is internal energy,
is internal energy,  is pressure, and
is pressure, and  is volume. Under the conditions of a Joule–Thomson expansion, the change in
is volume. Under the conditions of a Joule–Thomson expansion, the change in  represents the work done by the fluid (see the
represents the work done by the fluid (see the  . For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in
. For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in  with respect to pressure
with respect to pressure  , and its
, and its  as:
as:

 is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
 is
is
 must be
must be
 . Reproduced from Fig. 17 of .
. Reproduced from Fig. 17 of . with inversion temperature
with inversion temperature  .
.
 , and the relation between reduced pressure and reduced inversion temperature is
, and the relation between reduced pressure and reduced inversion temperature is 






 , defined by
, defined by
 .
.




