| John von Neumann | |
|---|---|
 von Neumann in the 1940s von Neumann in the 1940s | |
| Member of the United States Atomic Energy Commission | |
| In office March 15, 1955 – February 8, 1957 | |
| President | Dwight D. Eisenhower |
| Preceded by | Eugene M. Zuckert |
| Succeeded by | John S. Graham |
| Personal details | |
| Born | Neumann János Lajos (1903-12-28)December 28, 1903 Budapest, Kingdom of Hungary |
| Died | February 8, 1957(1957-02-08) (aged 53) Washington, D.C., U.S. |
| Resting place | Princeton Cemetery |
| Citizenship |
|
| Alma mater | |
| Known for | Mathematical formulation of quantum mechanics, Game theory, Spectral theory, Ergodic theory, von Neumann algebras, List of things named after John von Neumann |
| Spouses |
|
| Children | Marina von Neumann Whitman |
| Awards |
|
| Scientific career | |
| Fields | Logic, mathematics, mathematical physics, theoretical physics, statistics, economics, computer science, theoretical biology, chemistry, computing |
| Institutions | |
| Thesis | Az általános halmazelmélet axiomatikus felépítése (The axiomatic construction of general set theory) (1925) |
| Doctoral advisor | |
| Other academic advisors | |
| Doctoral students | |
| Other notable students | |
| Signature | |
John von Neumann (/vɒn ˈnɔɪmən/ von NOY-mən; Hungarian: Neumann János Lajos [ˈnɒjmɒn ˈjaːnoʃ ˈlɒjoʃ]; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, integrating pure and applied sciences and making major contributions to many fields, including mathematics, physics, economics, computing, and statistics. He was a pioneer in building the mathematical framework of quantum physics, in the development of functional analysis, and in game theory, introducing or codifying concepts including cellular automata, the universal constructor and the digital computer. His analysis of the structure of self-replication preceded the discovery of the structure of DNA.
During World War II, von Neumann worked on the Manhattan Project. He developed the mathematical models behind the explosive lenses used in the implosion-type nuclear weapon. Before and after the war, he consulted for many organizations including the Office of Scientific Research and Development, the Army's Ballistic Research Laboratory, the Armed Forces Special Weapons Project and the Oak Ridge National Laboratory. At the peak of his influence in the 1950s, he chaired a number of Defense Department committees including the Strategic Missile Evaluation Committee and the ICBM Scientific Advisory Committee. He was also a member of the influential Atomic Energy Commission in charge of all atomic energy development in the country. He played a key role alongside Bernard Schriever and Trevor Gardner in the design and development of the United States' first ICBM programs. At that time he was considered the nation's foremost expert on nuclear weaponry and the leading defense scientist at the U.S. Department of Defense.
Von Neumann's contributions and intellectual ability drew praise from colleagues in physics, mathematics, and beyond. Accolades he received range from the Medal of Freedom to a crater on the Moon named in his honor.
Life and education
Family background
Von Neumann was born in Budapest, Kingdom of Hungary (then part of the Austro-Hungarian Empire), on December 28, 1903, to a wealthy, non-observant Jewish family. His birth name was Neumann János Lajos. In Hungarian, the family name comes first, and his given names are equivalent to John Louis in English.
He was the eldest of three brothers; his two younger siblings were Mihály (Michael) and Miklós (Nicholas). His father Neumann Miksa (Max von Neumann) was a banker and held a doctorate in law. He had moved to Budapest from Pécs at the end of the 1880s. Miksa's father and grandfather were born in Ond (now part of Szerencs), Zemplén County, northern Hungary. John's mother was Kann Margit (Margaret Kann); her parents were Kann Jákab and Meisels Katalin of the Meisels family. Three generations of the Kann family lived in spacious apartments above the Kann-Heller offices in Budapest; von Neumann's family occupied an 18-room apartment on the top floor.
On February 20, 1913, Emperor Franz Joseph elevated John's father to the Hungarian nobility for his service to the Austro-Hungarian Empire. The Neumann family thus acquired the hereditary appellation Margittai, meaning "of Margitta" (today Marghita, Romania). The family had no connection with the town; the appellation was chosen in reference to Margaret, as was their chosen coat of arms depicting three marguerites. Neumann János became margittai Neumann János (John Neumann de Margitta), which he later changed to the German Johann von Neumann.
Child prodigy
Von Neumann was a child prodigy who at six years old could divide two eight-digit numbers in his head and converse in Ancient Greek. He, his brothers and his cousins were instructed by governesses. Von Neumann's father believed that knowledge of languages other than their native Hungarian was essential, so the children were tutored in English, French, German and Italian. By age eight, von Neumann was familiar with differential and integral calculus, and by twelve he had read Borel's La Théorie des Fonctions. He was also interested in history, reading Wilhelm Oncken's 46-volume world history series Allgemeine Geschichte in Einzeldarstellungen (General History in Monographs). One of the rooms in the apartment was converted into a library and reading room.
Von Neumann entered the Lutheran Fasori Evangélikus Gimnázium in 1914. Eugene Wigner was a year ahead of von Neumann at the school and soon became his friend.
Although von Neumann's father insisted that he attend school at the grade level appropriate to his age, he agreed to hire private tutors to give von Neumann advanced instruction. At 15, he began to study advanced calculus under the analyst Gábor Szegő. On their first meeting, Szegő was so astounded by von Neumann's mathematical talent and speed that, as recalled by his wife, he came back home with tears in his eyes. By 19, von Neumann had published two major mathematical papers, the second of which gave the modern definition of ordinal numbers, which superseded Georg Cantor's definition. At the conclusion of his education at the gymnasium, he applied for and won the Eötvös Prize, a national award for mathematics.
University studies
According to his friend Theodore von Kármán, von Neumann's father wanted John to follow him into industry, and asked von Kármán to persuade his son not to take mathematics. Von Neumann and his father decided that the best career path was chemical engineering. This was not something that von Neumann had much knowledge of, so it was arranged for him to take a two-year, non-degree course in chemistry at the University of Berlin, after which he sat for the entrance exam to ETH Zurich, which he passed in September 1923. Simultaneously von Neumann entered Pázmány Péter University, then known as the University of Budapest, as a Ph.D. candidate in mathematics. For his thesis, he produced an axiomatization of Cantor's set theory. In 1926, he graduated as a chemical engineer from ETH Zurich and simultaneously passed his final examinations summa cum laude for his Ph.D. in mathematics (with minors in experimental physics and chemistry) at the University of Budapest.
He then went to the University of Göttingen on a grant from the Rockefeller Foundation to study mathematics under David Hilbert. Hermann Weyl remembers how in the winter of 1926–1927 von Neumann, Emmy Noether, and he would walk through "the cold, wet, rain-wet streets of Göttingen" after class discussing hypercomplex number systems and their representations.
Career and private life

Von Neumann's habilitation was completed on December 13, 1927, and he began to give lectures as a Privatdozent at the University of Berlin in 1928. He was the youngest person elected Privatdozent in the university's history. He began writing nearly one major mathematics paper per month. In 1929, he briefly became a Privatdozent at the University of Hamburg, where the prospects of becoming a tenured professor were better, then in October of that year moved to Princeton University as a visiting lecturer in mathematical physics.
Von Neumann was baptized a Catholic in 1930. Shortly afterward, he married Marietta Kövesi, who had studied economics at Budapest University. Von Neumann and Marietta had a daughter, Marina, born in 1935; she would become a professor. The couple divorced on November 2, 1937. On November 17, 1938, von Neumann married Klára Dán.
In 1933 Von Neumann accepted a tenured professorship at the Institute for Advanced Study in New Jersey, when that institution's plan to appoint Hermann Weyl appeared to have failed. His mother, brothers and in-laws followed von Neumann to the United States in 1939. Von Neumann anglicized his name to John, keeping the German-aristocratic surname von Neumann. Von Neumann became a naturalized U.S. citizen in 1937, and immediately tried to become a lieutenant in the U.S. Army's Officers Reserve Corps. He passed the exams but was rejected because of his age.
Klára and John von Neumann were socially active within the local academic community. His white clapboard house on Westcott Road was one of Princeton's largest private residences. He always wore formal suits. He enjoyed Yiddish and "off-color" humor. In Princeton, he received complaints for playing extremely loud German march music; Von Neumann did some of his best work in noisy, chaotic environments. According to Churchill Eisenhart, von Neumann could attend parties until the early hours of the morning and then deliver a lecture at 8:30.
He was known for always being happy to provide others of all ability levels with scientific and mathematical advice. Wigner wrote that he perhaps supervised more work (in a casual sense) than any other modern mathematician. His daughter wrote that he was very concerned with his legacy in two aspects: his life and the durability of his intellectual contributions to the world.
Many considered him an excellent chairman of committees, deferring rather easily on personal or organizational matters but pressing on technical ones. Herbert York described the many "Von Neumann Committees" that he participated in as "remarkable in style as well as output". The way the committees von Neumann chaired worked directly and intimately with the necessary military or corporate entities became a blueprint for all Air Force long-range missile programs. Many people who had known von Neumann were puzzled by his relationship to the military and to power structures in general. Stanisław Ulam suspected that he had a hidden admiration for people or organizations that could influence the thoughts and decision making of others.
He also maintained his knowledge of languages learnt in his youth. He knew Hungarian, French, German and English fluently, and maintained a conversational level of Italian, Yiddish, Latin and Ancient Greek. His Spanish was less perfect. He had a passion for and encyclopedic knowledge of ancient history, and he enjoyed reading Ancient Greek historians in the original Greek. Ulam suspected they may have shaped his views on how future events could play out and how human nature and society worked in general.
Von Neumann's closest friend in the United States was the mathematician Stanisław Ulam. Von Neumann believed that much of his mathematical thought occurred intuitively; he would often go to sleep with a problem unsolved and know the answer upon waking up. Ulam noted that von Neumann's way of thinking might not be visual, but more aural. Ulam recalled, "Quite independently of his liking for abstract wit, he had a strong appreciation (one might say almost a hunger) for the more earthy type of comedy and humor".
Illness and death

In 1955, a mass was found near von Neumann's collarbone, which turned out to be cancer originating in the skeleton, pancreas or prostate. (While there is general agreement that the tumor had metastasised, sources differ on the location of the primary cancer.) The malignancy may have been caused by exposure to radiation at Los Alamos National Laboratory. As death neared he asked for a priest, though the priest later recalled that von Neumann found little comfort in receiving the last rites – he remained terrified of death and unable to accept it. Of his religious views, Von Neumann reportedly said, "So long as there is the possibility of eternal damnation for nonbelievers it is more logical to be a believer at the end," referring to Pascal's wager. He confided to his mother, "There probably has to be a God. Many things are easier to explain if there is than if there isn't."
He died Roman Catholic on February 8, 1957, at Walter Reed Army Medical Hospital and was buried at Princeton Cemetery.
Mathematics
Set theory
See also: Von Neumann–Bernays–Gödel set theory
At the beginning of the 20th century, efforts to base mathematics on naive set theory suffered a setback due to Russell's paradox (on the set of all sets that do not belong to themselves). The problem of an adequate axiomatization of set theory was resolved implicitly about twenty years later by Ernst Zermelo and Abraham Fraenkel. Zermelo–Fraenkel set theory provided a series of principles that allowed for the construction of the sets used in the everyday practice of mathematics, but did not explicitly exclude the possibility of the existence of a set that belongs to itself. In his 1925 doctoral thesis, von Neumann demonstrated two techniques to exclude such sets—the axiom of foundation and the notion of class.
The axiom of foundation proposed that every set can be constructed from the bottom up in an ordered succession of steps by way of the Zermelo–Fraenkel principles. If one set belongs to another, then the first must necessarily come before the second in the succession. This excludes the possibility of a set belonging to itself. To demonstrate that the addition of this new axiom to the others did not produce contradictions, von Neumann introduced the method of inner models, which became an essential demonstration instrument in set theory.
The second approach to the problem of sets belonging to themselves took as its base the notion of class, and defines a set as a class that belongs to other classes, while a proper class is defined as a class that does not belong to other classes. On the Zermelo–Fraenkel approach, the axioms impede the construction of a set of all sets that do not belong to themselves. In contrast, on von Neumann's approach, the class of all sets that do not belong to themselves can be constructed, but it is a proper class, not a set.
Overall, von Neumann's major achievement in set theory was an "axiomatization of set theory and (connected with that) elegant theory of the ordinal and cardinal numbers as well as the first strict formulation of principles of definitions by the transfinite induction".
Von Neumann paradox
Main article: Von Neumann paradoxBuilding on the Hausdorff paradox of Felix Hausdorff (1914), Stefan Banach and Alfred Tarski in 1924 showed how to subdivide a three-dimensional ball into disjoint sets, then translate and rotate these sets to form two identical copies of the same ball; this is the Banach–Tarski paradox. They also proved that a two-dimensional disk has no such paradoxical decomposition. But in 1929, von Neumann subdivided the disk into finitely many pieces and rearranged them into two disks, using area-preserving affine transformations instead of translations and rotations. The result depended on finding free groups of affine transformations, an important technique extended later by von Neumann in his work on measure theory.
Proof theory
See also: Hilbert's programWith the contributions of von Neumann to sets, the axiomatic system of the theory of sets avoided the contradictions of earlier systems and became usable as a foundation for mathematics, despite the lack of a proof of its consistency. The next question was whether it provided definitive answers to all mathematical questions that could be posed in it, or whether it might be improved by adding stronger axioms that could be used to prove a broader class of theorems.
By 1927, von Neumann was involving himself in discussions in Göttingen on whether elementary arithmetic followed from Peano axioms. Building on the work of Ackermann, he began attempting to prove (using the finistic methods of Hilbert's school) the consistency of first-order arithmetic. He succeeded in proving the consistency of a fragment of arithmetic of natural numbers (through the use of restrictions on induction). He continued looking for a more general proof of the consistency of classical mathematics using methods from proof theory.
A strongly negative answer to whether it was definitive arrived in September 1930 at the Second Conference on the Epistemology of the Exact Sciences, in which Kurt Gödel announced his first theorem of incompleteness: the usual axiomatic systems are incomplete, in the sense that they cannot prove every truth expressible in their language. Moreover, every consistent extension of these systems necessarily remains incomplete. At the conference, von Neumann suggested to Gödel that he should try to transform his results for undecidable propositions about integers.
Less than a month later, von Neumann communicated to Gödel an interesting consequence of his theorem: the usual axiomatic systems are unable to demonstrate their own consistency. Gödel replied that he had already discovered this consequence, now known as his second incompleteness theorem, and that he would send a preprint of his article containing both results, which never appeared. Von Neumann acknowledged Gödel's priority in his next letter. However, von Neumann's method of proof differed from Gödel's, and he was also of the opinion that the second incompleteness theorem had dealt a much stronger blow to Hilbert's program than Gödel thought it did. With this discovery, which drastically changed his views on mathematical rigor, von Neumann ceased research in the foundations of mathematics and metamathematics and instead spent time on problems connected with applications.
Ergodic theory
In a series of papers published in 1932, von Neumann made foundational contributions to ergodic theory, a branch of mathematics that involves the states of dynamical systems with an invariant measure. Of the 1932 papers on ergodic theory, Paul Halmos wrote that even "if von Neumann had never done anything else, they would have been sufficient to guarantee him mathematical immortality". By then von Neumann had already written his articles on operator theory, and the application of this work was instrumental in his mean ergodic theorem.
The theorem is about arbitrary one-parameter unitary groups and states that for every vector in the Hilbert space, exists in the sense of the metric defined by the Hilbert norm and is a vector which is such that for all . This was proven in the first paper. In the second paper, von Neumann argued that his results here were sufficient for physical applications relating to Boltzmann's ergodic hypothesis. He also pointed out that ergodicity had not yet been achieved and isolated this for future work.
Later in the year he published another influential paper that began the systematic study of ergodicity. He gave and proved a decomposition theorem showing that the ergodic measure preserving actions of the real line are the fundamental building blocks from which all measure preserving actions can be built. Several other key theorems are given and proven. The results in this paper and another in conjunction with Paul Halmos have significant applications in other areas of mathematics.
Measure theory
See also: Lifting theoryIn measure theory, the "problem of measure" for an n-dimensional Euclidean space R may be stated as: "does there exist a positive, normalized, invariant, and additive set function on the class of all subsets of R?" The work of Felix Hausdorff and Stefan Banach had implied that the problem of measure has a positive solution if n = 1 or n = 2 and a negative solution (because of the Banach–Tarski paradox) in all other cases. Von Neumann's work argued that the "problem is essentially group-theoretic in character": the existence of a measure could be determined by looking at the properties of the transformation group of the given space. The positive solution for spaces of dimension at most two, and the negative solution for higher dimensions, comes from the fact that the Euclidean group is a solvable group for dimension at most two, and is not solvable for higher dimensions. "Thus, according to von Neumann, it is the change of group that makes a difference, not the change of space." Around 1942 he told Dorothy Maharam how to prove that every complete σ-finite measure space has a multiplicative lifting; he did not publish this proof and she later came up with a new one.
In a number of von Neumann's papers, the methods of argument he employed are considered even more significant than the results. In anticipation of his later study of dimension theory in algebras of operators, von Neumann used results on equivalence by finite decomposition, and reformulated the problem of measure in terms of functions. A major contribution von Neumann made to measure theory was the result of a paper written to answer a question of Haar regarding whether there existed an algebra of all bounded functions on the real number line such that they form "a complete system of representatives of the classes of almost everywhere-equal measurable bounded functions". He proved this in the positive, and in later papers with Stone discussed various generalizations and algebraic aspects of this problem. He also proved by new methods the existence of disintegrations for various general types of measures. Von Neumann also gave a new proof on the uniqueness of Haar measures by using the mean values of functions, although this method only worked for compact groups. He had to create entirely new techniques to apply this to locally compact groups. He also gave a new, ingenious proof for the Radon–Nikodym theorem. His lecture notes on measure theory at the Institute for Advanced Study were an important source for knowledge on the topic in America at the time, and were later published.
Topological groups
Using his previous work on measure theory, von Neumann made several contributions to the theory of topological groups, beginning with a paper on almost periodic functions on groups, where von Neumann extended Bohr's theory of almost periodic functions to arbitrary groups. He continued this work with another paper in conjunction with Bochner that improved the theory of almost periodicity to include functions that took on elements of linear spaces as values rather than numbers. In 1938, he was awarded the Bôcher Memorial Prize for his work in analysis in relation to these papers.
In a 1933 paper, he used the newly discovered Haar measure in the solution of Hilbert's fifth problem for the case of compact groups. The basic idea behind this was discovered several years earlier when von Neumann published a paper on the analytic properties of groups of linear transformations and found that closed subgroups of a general linear group are Lie groups. This was later extended by Cartan to arbitrary Lie groups in the form of the closed-subgroup theorem.
Functional analysis
Main article: Operator theorySee also: Spectral theoremVon Neumann was the first to axiomatically define an abstract Hilbert space. He defined it as a complex vector space with a Hermitian scalar product, with the corresponding norm being both separable and complete. In the same papers he also proved the general form of the Cauchy–Schwarz inequality that had previously been known only in specific examples. He continued with the development of the spectral theory of operators in Hilbert space in three seminal papers between 1929 and 1932. This work cumulated in his Mathematical Foundations of Quantum Mechanics which alongside two other books by Stone and Banach in the same year were the first monographs on Hilbert space theory. Previous work by others showed that a theory of weak topologies could not be obtained by using sequences. Von Neumann was the first to outline a program of how to overcome the difficulties, which resulted in him defining locally convex spaces and topological vector spaces for the first time. In addition several other topological properties he defined at the time (he was among the first mathematicians to apply new topological ideas from Hausdorff from Euclidean to Hilbert spaces) such as boundness and total boundness are still used today. For twenty years von Neumann was considered the 'undisputed master' of this area. These developments were primarily prompted by needs in quantum mechanics where von Neumann realized the need to extend the spectral theory of Hermitian operators from the bounded to the unbounded case. Other major achievements in these papers include a complete elucidation of spectral theory for normal operators, the first abstract presentation of the trace of a positive operator, a generalisation of Riesz's presentation of Hilbert's spectral theorems at the time, and the discovery of Hermitian operators in a Hilbert space, as distinct from self-adjoint operators, which enabled him to give a description of all Hermitian operators which extend a given Hermitian operator. He wrote a paper detailing how the usage of infinite matrices, common at the time in spectral theory, was inadequate as a representation for Hermitian operators. His work on operator theory lead to his most profound invention in pure mathematics, the study of von Neumann algebras and in general of operator algebras.
His later work on rings of operators lead to him revisiting his work on spectral theory and providing a new way of working through the geometric content by the use of direct integrals of Hilbert spaces. Like in his work on measure theory he proved several theorems that he did not find time to publish. He told Nachman Aronszajn and K. T. Smith that in the early 1930s he proved the existence of proper invariant subspaces for completely continuous operators in a Hilbert space while working on the invariant subspace problem.
With I. J. Schoenberg he wrote several items investigating translation invariant Hilbertian metrics on the real number line which resulted in their complete classification. Their motivation lie in various questions related to embedding metric spaces into Hilbert spaces.
With Pascual Jordan he wrote a short paper giving the first derivation of a given norm from an inner product by means of the parallelogram identity. His trace inequality is a key result of matrix theory used in matrix approximation problems. He also first presented the idea that the dual of a pre-norm is a norm in the first major paper discussing the theory of unitarily invariant norms and symmetric gauge functions (now known as symmetric absolute norms). This paper leads naturally to the study of symmetric operator ideals and is the beginning point for modern studies of symmetric operator spaces.
Later with Robert Schatten he initiated the study of nuclear operators on Hilbert spaces, tensor products of Banach spaces, introduced and studied trace class operators, their ideals, and their duality with compact operators, and preduality with bounded operators. The generalization of this topic to the study of nuclear operators on Banach spaces was among the first achievements of Alexander Grothendieck. Previously in 1937 von Neumann published several results in this area, for example giving 1-parameter scale of different cross norms on and proving several other results on what are now known as Schatten–von Neumann ideals.
Operator algebras
Main article: Von Neumann algebraSee also: Direct integralVon Neumann founded the study of rings of operators, through the von Neumann algebras (originally called W*-algebras). While his original ideas for rings of operators existed already in 1930, he did not begin studying them in depth until he met F. J. Murray several years later. A von Neumann algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. The von Neumann bicommutant theorem shows that the analytic definition is equivalent to a purely algebraic definition as being equal to the bicommutant. After elucidating the study of the commutative algebra case, von Neumann embarked in 1936, with the partial collaboration of Murray, on the noncommutative case, the general study of factors classification of von Neumann algebras. The six major papers in which he developed that theory between 1936 and 1940 "rank among the masterpieces of analysis in the twentieth century"; they collect many foundational results and started several programs in operator algebra theory that mathematicians worked on for decades afterwards. An example is the classification of factors. In addition in 1938 he proved that every von Neumann algebra on a separable Hilbert space is a direct integral of factors; he did not find time to publish this result until 1949. Von Neumann algebras relate closely to a theory of noncommutative integration, something that von Neumann hinted to in his work but did not explicitly write out. Another important result on polar decomposition was published in 1932.
Lattice theory
Main article: Continuous geometrySee also: Complemented lattice § Orthomodular latticesBetween 1935 and 1937, von Neumann worked on lattice theory, the theory of partially ordered sets in which every two elements have a greatest lower bound and a least upper bound. As Garrett Birkhoff wrote, "John von Neumann's brilliant mind blazed over lattice theory like a meteor". Von Neumann combined traditional projective geometry with modern algebra (linear algebra, ring theory, lattice theory). Many previously geometric results could then be interpreted in the case of general modules over rings. His work laid the foundations for some of the modern work in projective geometry.
His biggest contribution was founding the field of continuous geometry. It followed his path-breaking work on rings of operators. In mathematics, continuous geometry is a substitute of complex projective geometry, where instead of the dimension of a subspace being in a discrete set it can be an element of the unit interval . Earlier, Menger and Birkhoff had axiomatized complex projective geometry in terms of the properties of its lattice of linear subspaces. Von Neumann, following his work on rings of operators, weakened those axioms to describe a broader class of lattices, the continuous geometries.
While the dimensions of the subspaces of projective geometries are a discrete set (the non-negative integers), the dimensions of the elements of a continuous geometry can range continuously across the unit interval . Von Neumann was motivated by his discovery of von Neumann algebras with a dimension function taking a continuous range of dimensions, and the first example of a continuous geometry other than projective space was the projections of the hyperfinite type II factor.
In more pure lattice theoretical work, he solved the difficult problem of characterizing the class of (continuous-dimensional projective geometry over an arbitrary division ring ) in abstract language of lattice theory. Von Neumann provided an abstract exploration of dimension in completed complemented modular topological lattices (properties that arise in the lattices of subspaces of inner product spaces):
Dimension is determined, up to a positive linear transformation, by the following two properties. It is conserved by perspective mappings ("perspectivities") and ordered by inclusion. The deepest part of the proof concerns the equivalence of perspectivity with "projectivity by decomposition"—of which a corollary is the transitivity of perspectivity.
For any integer every -dimensional abstract projective geometry is isomorphic to the subspace-lattice of an -dimensional vector space over a (unique) corresponding division ring . This is known as the Veblen–Young theorem. Von Neumann extended this fundamental result in projective geometry to the continuous dimensional case. This coordinatization theorem stimulated considerable work in abstract projective geometry and lattice theory, much of which continued using von Neumann's techniques. Birkhoff described this theorem as follows:
Any complemented modular lattice L having a "basis" of n ≥ 4 pairwise perspective elements, is isomorphic with the lattice ℛ(R) of all principal right-ideals of a suitable regular ring R. This conclusion is the culmination of 140 pages of brilliant and incisive algebra involving entirely novel axioms. Anyone wishing to get an unforgettable impression of the razor edge of von Neumann's mind, need merely try to pursue this chain of exact reasoning for himself—realizing that often five pages of it were written down before breakfast, seated at a living room writing-table in a bathrobe.
This work required the creation of regular rings. A von Neumann regular ring is a ring where for every , an element exists such that . These rings came from and have connections to his work on von Neumann algebras, as well as AW*-algebras and various kinds of C*-algebras.
Many smaller technical results were proven during the creation and proof of the above theorems, particularly regarding distributivity (such as infinite distributivity), von Neumann developing them as needed. He also developed a theory of valuations in lattices, and shared in developing the general theory of metric lattices.
Birkhoff noted in his posthumous article on von Neumann that most of these results were developed in an intense two-year period of work, and that while his interests continued in lattice theory after 1937, they became peripheral and mainly occurred in letters to other mathematicians. A final contribution in 1940 was for a joint seminar he conducted with Birkhoff at the Institute for Advanced Study on the subject where he developed a theory of σ-complete lattice ordered rings. He never wrote up the work for publication.
Mathematical statistics
Von Neumann made fundamental contributions to mathematical statistics. In 1941, he derived the exact distribution of the ratio of the mean square of successive differences to the sample variance for independent and identically normally distributed variables. This ratio was applied to the residuals from regression models and is commonly known as the Durbin–Watson statistic for testing the null hypothesis that the errors are serially independent against the alternative that they follow a stationary first order autoregression.
Subsequently, Denis Sargan and Alok Bhargava extended the results for testing whether the errors on a regression model follow a Gaussian random walk (i.e., possess a unit root) against the alternative that they are a stationary first order autoregression.
Other work
In his early years, von Neumann published several papers related to set-theoretical real analysis and number theory. In a paper from 1925, he proved that for any dense sequence of points in , there existed a rearrangement of those points that is uniformly distributed. In 1926 his sole publication was on Prüfer's theory of ideal algebraic numbers where he found a new way of constructing them, thus extending Prüfer's theory to the field of all algebraic numbers, and clarified their relation to p-adic numbers. In 1928 he published two additional papers continuing with these themes. The first dealt with partitioning an interval into countably many congruent subsets. It solved a problem of Hugo Steinhaus asking whether an interval is -divisible. Von Neumann proved that indeed that all intervals, half-open, open, or closed are -divisible by translations (i.e. that these intervals can be decomposed into subsets that are congruent by translation). His next paper dealt with giving a constructive proof without the axiom of choice that algebraically independent reals exist. He proved that are algebraically independent for . Consequently, there exists a perfect algebraically independent set of reals the size of the continuum. Other minor results from his early career include a proof of a maximum principle for the gradient of a minimizing function in the field of calculus of variations, and a small simplification of Hermann Minkowski's theorem for linear forms in geometric number theory. Later in his career together with Pascual Jordan and Eugene Wigner he wrote a foundational paper classifying all finite-dimensional formally real Jordan algebras and discovering the Albert algebras while attempting to look for a better mathematical formalism for quantum theory. In 1936 he attempted to further the program of replacing the axioms of his previous Hilbert space program with those of Jordan algebras in a paper investigating the infinite-dimensional case; he planned to write at least one further paper on the topic but never did. Nevertheless, these axioms formed the basis for further investigations of algebraic quantum mechanics started by Irving Segal.
Physics
Quantum mechanics
See also: Quantum mutual information, Measurement in quantum mechanics, and Wave function collapseVon Neumann was the first to establish a rigorous mathematical framework for quantum mechanics, known as the Dirac–von Neumann axioms, in his influential 1932 work Mathematical Foundations of Quantum Mechanics. After having completed the axiomatization of set theory, he began to confront the axiomatization of quantum mechanics. He realized in 1926 that a state of a quantum system could be represented by a point in a (complex) Hilbert space that, in general, could be infinite-dimensional even for a single particle. In this formalism of quantum mechanics, observable quantities such as position or momentum are represented as linear operators acting on the Hilbert space associated with the quantum system.
The physics of quantum mechanics was thereby reduced to the mathematics of Hilbert spaces and linear operators acting on them. For example, the uncertainty principle, according to which the determination of the position of a particle prevents the determination of its momentum and vice versa, is translated into the non-commutativity of the two corresponding operators. This new mathematical formulation included as special cases the formulations of both Heisenberg and Schrödinger.
Von Neumann's abstract treatment permitted him to confront the foundational issue of determinism versus non-determinism, and in the book he presented a proof that the statistical results of quantum mechanics could not possibly be averages of an underlying set of determined "hidden variables", as in classical statistical mechanics. In 1935, Grete Hermann published a paper arguing that the proof contained a conceptual error and was therefore invalid. Hermann's work was largely ignored until after John S. Bell made essentially the same argument in 1966. In 2010, Jeffrey Bub argued that Bell had misconstrued von Neumann's proof, and pointed out that the proof, though not valid for all hidden variable theories, does rule out a well-defined and important subset. Bub also suggests that von Neumann was aware of this limitation and did not claim that his proof completely ruled out hidden variable theories. The validity of Bub's argument is, in turn, disputed. Gleason's theorem of 1957 provided an argument against hidden variables along the lines of von Neumann's, but founded on assumptions seen as better motivated and more physically meaningful.
Von Neumann's proof inaugurated a line of research that ultimately led, through Bell's theorem and the experiments of Alain Aspect in 1982, to the demonstration that quantum physics either requires a notion of reality substantially different from that of classical physics, or must include nonlocality in apparent violation of special relativity.
In a chapter of The Mathematical Foundations of Quantum Mechanics, von Neumann deeply analyzed the so-called measurement problem. He concluded that the entire physical universe could be made subject to the universal wave function. Since something "outside the calculation" was needed to collapse the wave function, von Neumann concluded that the collapse was caused by the consciousness of the experimenter. He argued that the mathematics of quantum mechanics allows the collapse of the wave function to be placed at any position in the causal chain from the measurement device to the "subjective consciousness" of the human observer. In other words, while the line between observer and observed could be drawn in different places, the theory only makes sense if an observer exists somewhere. Although the idea of consciousness causing collapse was accepted by Eugene Wigner, the Von Neumann–Wigner interpretation never gained acceptance among the majority of physicists.
Though theories of quantum mechanics continue to evolve, a basic framework for the mathematical formalism of problems in quantum mechanics underlying most approaches can be traced back to the mathematical formalisms and techniques first used by von Neumann. Discussions about interpretation of the theory, and extensions to it, are now mostly conducted on the basis of shared assumptions about the mathematical foundations.
Viewing von Neumann's work on quantum mechanics as a part of the fulfilment of Hilbert's sixth problem, mathematical physicist Arthur Wightman said in 1974 his axiomization of quantum theory was perhaps the most important axiomization of a physical theory to date. With his 1932 book, quantum mechanics became a mature theory in the sense it had a precise mathematical form, which allowed for clear answers to conceptual problems. Nevertheless, von Neumann in his later years felt he had failed in this aspect of his scientific work as despite all the mathematics he developed, he did not find a satisfactory mathematical framework for quantum theory as a whole.
Von Neumann entropy
Main article: Von Neumann entropyVon Neumann entropy is extensively used in different forms (conditional entropy, relative entropy, etc.) in the framework of quantum information theory. Entanglement measures are based upon some quantity directly related to the von Neumann entropy. Given a statistical ensemble of quantum mechanical systems with the density matrix , it is given by Many of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and conditional quantum entropy. Quantum information theory is largely concerned with the interpretation and uses of von Neumann entropy, a cornerstone in the former's development; the Shannon entropy applies to classical information theory.
Density matrix
Main article: Density matrixThe formalism of density operators and matrices was introduced by von Neumann in 1927 and independently, but less systematically by Lev Landau and Felix Bloch in 1927 and 1946 respectively. The density matrix allows the representation of probabilistic mixtures of quantum states (mixed states) in contrast to wavefunctions, which can only represent pure states.
Von Neumann measurement scheme
The von Neumann measurement scheme, the ancestor of quantum decoherence theory, represents measurements projectively by taking into account the measuring apparatus which is also treated as a quantum object. The 'projective measurement' scheme introduced by von Neumann led to the development of quantum decoherence theories.
Quantum logic
Main article: Quantum logicVon Neumann first proposed a quantum logic in his 1932 treatise Mathematical Foundations of Quantum Mechanics, where he noted that projections on a Hilbert space can be viewed as propositions about physical observables. The field of quantum logic was subsequently inaugurated in a 1936 paper by von Neumann and Garrett Birkhoff, the first to introduce quantum logics, wherein von Neumann and Birkhoff first proved that quantum mechanics requires a propositional calculus substantially different from all classical logics and rigorously isolated a new algebraic structure for quantum logics. The concept of creating a propositional calculus for quantum logic was first outlined in a short section in von Neumann's 1932 work, but in 1936, the need for the new propositional calculus was demonstrated through several proofs. For example, photons cannot pass through two successive filters that are polarized perpendicularly (e.g., horizontally and vertically), and therefore, a fortiori, it cannot pass if a third filter polarized diagonally is added to the other two, either before or after them in the succession, but if the third filter is added between the other two, the photons will indeed pass through. This experimental fact is translatable into logic as the non-commutativity of conjunction . It was also demonstrated that the laws of distribution of classical logic, and , are not valid for quantum theory.
The reason for this is that a quantum disjunction, unlike the case for classical disjunction, can be true even when both of the disjuncts are false and this is in turn attributable to the fact that it is frequently the case in quantum mechanics that a pair of alternatives are semantically determinate, while each of its members is necessarily indeterminate. Consequently, the distributive law of classical logic must be replaced with a weaker condition. Instead of a distributive lattice, propositions about a quantum system form an orthomodular lattice isomorphic to the lattice of subspaces of the Hilbert space associated with that system.
Nevertheless, he was never satisfied with his work on quantum logic. He intended it to be a joint synthesis of formal logic and probability theory and when he attempted to write up a paper for the Henry Joseph Lecture he gave at the Washington Philosophical Society in 1945 he found that he could not, especially given that he was busy with war work at the time. During his address at the 1954 International Congress of Mathematicians he gave this issue as one of the unsolved problems that future mathematicians could work on.
Fluid dynamics
Von Neumann made fundamental contributions in the field of fluid dynamics, including the classic flow solution to blast waves, and the co-discovery (independently by Yakov Borisovich Zel'dovich and Werner Döring) of the ZND detonation model of explosives. During the 1930s, von Neumann became an authority on the mathematics of shaped charges.
Later with Robert D. Richtmyer, von Neumann developed an algorithm defining artificial viscosity that improved the understanding of shock waves. When computers solved hydrodynamic or aerodynamic problems, they put too many computational grid points at regions of sharp discontinuity (shock waves). The mathematics of artificial viscosity smoothed the shock transition without sacrificing basic physics.
Von Neumann soon applied computer modelling to the field, developing software for his ballistics research. During World War II, he approached R. H. Kent, the director of the US Army's Ballistic Research Laboratory, with a computer program for calculating a one-dimensional model of 100 molecules to simulate a shock wave. Von Neumann gave a seminar on his program to an audience which included his friend Theodore von Kármán. After von Neumann had finished, von Kármán said "Of course you realize Lagrange also used digital models to simulate continuum mechanics." Von Neumann had been unaware of Lagrange's Mécanique analytique.
Other work

While not as prolific in physics as he was in mathematics, he nevertheless made several other notable contributions. His pioneering papers with Subrahmanyan Chandrasekhar on the statistics of a fluctuating gravitational field generated by randomly distributed stars were considered a tour de force. In this paper they developed a theory of two-body relaxation and used the Holtsmark distribution to model the dynamics of stellar systems. He wrote several other unpublished manuscripts on topics in stellar structure, some of which were included in Chandrasekhar's other works. In earlier work led by Oswald Veblen von Neumann helped develop basic ideas involving spinors that would lead to Roger Penrose's twistor theory. Much of this was done in seminars conducted at the IAS during the 1930s. From this work he wrote a paper with A. H. Taub and Veblen extending the Dirac equation to projective relativity, with a key focus on maintaining invariance with regards to coordinate, spin, and gauge transformations, as a part of early research into potential theories of quantum gravity in the 1930s. In the same time period he made several proposals to colleagues for dealing with the problems in the newly created quantum field theory and for quantizing spacetime; however, both his colleagues and he did not consider the ideas fruitful and did not pursue them. Nevertheless, he maintained at least some interest, in 1940 writing a manuscript on the Dirac equation in de Sitter space.
Economics
Game theory
Von Neumann founded the field of game theory as a mathematical discipline. He proved his minimax theorem in 1928. It establishes that in zero-sum games with perfect information (i.e., in which players know at each time all moves that have taken place so far), there exists a pair of strategies for both players that allows each to minimize their maximum losses. Such strategies are called optimal. Von Neumann showed that their minimaxes are equal (in absolute value) and contrary (in sign). He improved and extended the minimax theorem to include games involving imperfect information and games with more than two players, publishing this result in his 1944 Theory of Games and Economic Behavior, written with Oskar Morgenstern. The public interest in this work was such that The New York Times ran a front-page story. In this book, von Neumann declared that economic theory needed to use functional analysis, especially convex sets and the topological fixed-point theorem, rather than the traditional differential calculus, because the maximum-operator did not preserve differentiable functions.
Von Neumann's functional-analytic techniques—the use of duality pairings of real vector spaces to represent prices and quantities, the use of supporting and separating hyperplanes and convex sets, and fixed-point theory—have been primary tools of mathematical economics ever since.
Mathematical economics
Von Neumann raised the mathematical level of economics in several influential publications. For his model of an expanding economy, he proved the existence and uniqueness of an equilibrium using his generalization of the Brouwer fixed-point theorem. Von Neumann's model of an expanding economy considered the matrix pencil A − λB with nonnegative matrices A and B; von Neumann sought probability vectors p and q and a positive number λ that would solve the complementarity equation along with two inequality systems expressing economic efficiency. In this model, the (transposed) probability vector p represents the prices of the goods while the probability vector q represents the "intensity" at which the production process would run. The unique solution λ represents the growth factor which is 1 plus the rate of growth of the economy; the rate of growth equals the interest rate.
Von Neumann's results have been viewed as a special case of linear programming, where his model uses only nonnegative matrices. The study of his model of an expanding economy continues to interest mathematical economists. This paper has been called the greatest paper in mathematical economics by several authors, who recognized its introduction of fixed-point theorems, linear inequalities, complementary slackness, and saddlepoint duality. In the proceedings of a conference on von Neumann's growth model, Paul Samuelson said that many mathematicians had developed methods useful to economists, but that von Neumann was unique in having made significant contributions to economic theory itself. The lasting importance of the work on general equilibria and the methodology of fixed point theorems is underscored by the awarding of Nobel prizes in 1972 to Kenneth Arrow, in 1983 to Gérard Debreu, and in 1994 to John Nash who used fixed point theorems to establish equilibria for non-cooperative games and for bargaining problems in his Ph.D. thesis. Arrow and Debreu also used linear programming, as did Nobel laureates Tjalling Koopmans, Leonid Kantorovich, Wassily Leontief, Paul Samuelson, Robert Dorfman, Robert Solow, and Leonid Hurwicz.
Von Neumann's interest in the topic began while he was lecturing at Berlin in 1928 and 1929. He spent his summers in Budapest, as did the economist Nicholas Kaldor; Kaldor recommended that von Neumann read a book by the mathematical economist Léon Walras. Von Neumann noticed that Walras's General Equilibrium Theory and Walras's law, which led to systems of simultaneous linear equations, could produce the absurd result that profit could be maximized by producing and selling a negative quantity of a product. He replaced the equations by inequalities, introduced dynamic equilibria, among other things, and eventually produced his paper.
Linear programming
Building on his results on matrix games and on his model of an expanding economy, von Neumann invented the theory of duality in linear programming when George Dantzig described his work in a few minutes, and an impatient von Neumann asked him to get to the point. Dantzig then listened dumbfounded while von Neumann provided an hourlong lecture on convex sets, fixed-point theory, and duality, conjecturing the equivalence between matrix games and linear programming.
Later, von Neumann suggested a new method of linear programming, using the homogeneous linear system of Paul Gordan (1873), which was later popularized by Karmarkar's algorithm. Von Neumann's method used a pivoting algorithm between simplices, with the pivoting decision determined by a nonnegative least squares subproblem with a convexity constraint (projecting the zero-vector onto the convex hull of the active simplex). Von Neumann's algorithm was the first interior point method of linear programming.
Computer science
Von Neumann was a founding figure in computing, with significant contributions to computing hardware design, to theoretical computer science, to scientific computing, and to the philosophy of computer science.
Hardware

Von Neumann consulted for the Army's Ballistic Research Laboratory, most notably on the ENIAC project, as a member of its Scientific Advisory Committee. Although the single-memory, stored-program architecture is commonly called von Neumann architecture, the architecture was based on the work of J. Presper Eckert and John Mauchly, inventors of ENIAC and its successor, EDVAC. While consulting for the EDVAC project at the University of Pennsylvania, von Neumann wrote an incomplete First Draft of a Report on the EDVAC. The paper, whose premature distribution nullified the patent claims of Eckert and Mauchly, described a computer that stored both its data and its program in the same address space, unlike the earliest computers which stored their programs separately on paper tape or plugboards. This architecture became the basis of most modern computer designs.
Next, von Neumann designed the IAS machine at the Institute for Advanced Study in Princeton, New Jersey. He arranged its financing, and the components were designed and built at the RCA Research Laboratory nearby. Von Neumann recommended that the IBM 701, nicknamed the defense computer, include a magnetic drum. It was a faster version of the IAS machine and formed the basis for the commercially successful IBM 704.
Algorithms
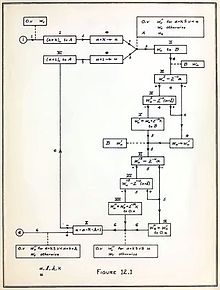
Von Neumann was the inventor, in 1945, of the merge sort algorithm, in which the first and second halves of an array are each sorted recursively and then merged.
As part of Von Neumann's hydrogen bomb work, he and Stanisław Ulam developed simulations for hydrodynamic computations. He also contributed to the development of the Monte Carlo method, which used random numbers to approximate the solutions to complicated problems.
Von Neumann's algorithm for simulating a fair coin with a biased coin is used in the "software whitening" stage of some hardware random number generators. Because obtaining "truly" random numbers was impractical, von Neumann developed a form of pseudorandomness, using the middle-square method. He justified this crude method as faster than any other method at his disposal, writing that "Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin." He also noted that when this method went awry it did so obviously, unlike other methods which could be subtly incorrect.
Stochastic computing was introduced by von Neumann in 1953, but could not be implemented until advances in computing of the 1960s. Around 1950 he was also among the first to talk about the time complexity of computations, which eventually evolved into the field of computational complexity theory.
Cellular automata, DNA and the universal constructor
See also: von Neumann cellular automaton, von Neumann universal constructor, von Neumann neighborhood, and von Neumann Probe

Von Neumann's mathematical analysis of the structure of self-replication preceded the discovery of the structure of DNA. Ulam and von Neumann are also generally credited with creating the field of cellular automata, beginning in the 1940s, as a simplified mathematical model of biological systems.
In lectures in 1948 and 1949, von Neumann proposed a kinematic self-reproducing automaton. By 1952, he was treating the problem more abstractly. He designed an elaborate 2D cellular automaton that would automatically make a copy of its initial configuration of cells. The Von Neumann universal constructor based on the von Neumann cellular automaton was fleshed out in his posthumous Theory of Self Reproducing Automata. The von Neumann neighborhood, in which each cell in a two-dimensional grid has the four orthogonally adjacent grid cells as neighbors, continues to be used for other cellular automata.
Scientific computing and numerical analysis
Considered to be possibly "the most influential researcher in scientific computing of all time", von Neumann made several contributions to the field, both technically and administratively. He developed the Von Neumann stability analysis procedure, still commonly used to avoid errors from building up in numerical methods for linear partial differential equations. His paper with Herman Goldstine in 1947 was the first to describe backward error analysis, although implicitly. He was also one of the first to write about the Jacobi method. At Los Alamos, he wrote several classified reports on solving problems of gas dynamics numerically. However, he was frustrated by the lack of progress with analytic methods for these nonlinear problems. As a result, he turned towards computational methods. Under his influence Los Alamos became the leader in computational science during the 1950s and early 1960s.
From this work von Neumann realized that computation was not just a tool to brute force the solution to a problem numerically, but could also provide insight for solving problems analytically, and that there was an enormous variety of scientific and engineering problems towards which computers would be useful, most significant of which were nonlinear problems. In June 1945 at the First Canadian Mathematical Congress he gave his first talk on general ideas of how to solve problems, particularly of fluid dynamics numerically. He also described how wind tunnels were actually analog computers, and how digital computers would replace them and bring a new era of fluid dynamics. Garrett Birkhoff described it as "an unforgettable sales pitch". He expanded this talk with Goldstine into the manuscript "On the Principles of Large Scale Computing Machines" and used it to promote the support of scientific computing. His papers also developed the concepts of inverting matrices, random matrices and automated relaxation methods for solving elliptic boundary value problems.
Weather systems and global warming
See also: History of numerical weather prediction and History of climate change science § Increasing concern, 1950s–1960sAs part of his research into possible applications of computers, von Neumann became interested in weather prediction, noting similarities between the problems in the field and those he had worked on during the Manhattan Project. In 1946 von Neumann founded the "Meteorological Project" at the Institute for Advanced Study, securing funding for his project from the Weather Bureau, the US Air Force and US Navy weather services. With Carl-Gustaf Rossby, considered the leading theoretical meteorologist at the time, he gathered a group of twenty meteorologists to work on various problems in the field. However, given his other postwar work he was not able to devote enough time to proper leadership of the project and little was accomplished.
This changed when a young Jule Gregory Charney took up co-leadership of the project from Rossby. By 1950 von Neumann and Charney wrote the world's first climate modelling software, and used it to perform the world's first numerical weather forecasts on the ENIAC computer that von Neumann had arranged to be used; von Neumann and his team published the results as Numerical Integration of the Barotropic Vorticity Equation. Together they played a leading role in efforts to integrate sea-air exchanges of energy and moisture into the study of climate. Though primitive, news of the ENIAC forecasts quickly spread around the world and a number of parallel projects in other locations were initiated.
In 1955 von Neumann, Charney and their collaborators convinced their funders to open the Joint Numerical Weather Prediction Unit (JNWPU) in Suitland, Maryland, which began routine real-time weather forecasting. Next up, von Neumann proposed a research program for climate modeling:
The approach is to first try short-range forecasts, then long-range forecasts of those properties of the circulation that can perpetuate themselves over arbitrarily long periods of time, and only finally to attempt forecast for medium-long time periods which are too long to treat by simple hydrodynamic theory and too short to treat by the general principle of equilibrium theory.
Positive results of Norman A. Phillips in 1955 prompted immediate reaction and von Neumann organized a conference at Princeton on "Application of Numerical Integration Techniques to the Problem of the General Circulation". Once again he strategically organized the program as a predictive one to ensure continued support from the Weather Bureau and the military, leading to the creation of the General Circulation Research Section (now the Geophysical Fluid Dynamics Laboratory) next to the JNWPU. He continued work both on technical issues of modelling and in ensuring continuing funding for these projects. During the late 19th century, Svante Arrhenius suggested that human activity could cause global warming by adding carbon dioxide to the atmosphere. In 1955, von Neumann observed that this may already have begun: "Carbon dioxide released into the atmosphere by industry's burning of coal and oil – more than half of it during the last generation – may have changed the atmosphere's composition sufficiently to account for a general warming of the world by about one degree Fahrenheit." His research into weather systems and meteorological prediction led him to propose manipulating the environment by spreading colorants on the polar ice caps to enhance absorption of solar radiation (by reducing the albedo). However, he urged caution in any program of atmosphere modification:
What could be done, of course, is no index to what should be done... In fact, to evaluate the ultimate consequences of either a general cooling or a general heating would be a complex matter. Changes would affect the level of the seas, and hence the habitability of the continental coastal shelves; the evaporation of the seas, and hence general precipitation and glaciation levels; and so on... But there is little doubt that one could carry out the necessary analyses needed to predict the results, intervene on any desired scale, and ultimately achieve rather fantastic results.
He also warned that weather and climate control could have military uses, telling Congress in 1956 that they could pose an even bigger risk than ICBMs.
Technological singularity hypothesis
See also: Technological singularity—von Neumann, 1955"The technology that is now developing and that will dominate the next decades is in conflict with traditional, and, in the main, momentarily still valid, geographical and political units and concepts. This is a maturing crisis of technology... The most hopeful answer is that the human species has been subjected to similar tests before and it seems to have a congenital ability to come through, after varying amounts of trouble."
The first use of the concept of a singularity in the technological context is attributed to von Neumann, who according to Ulam discussed the "ever accelerating progress of technology and changes in the mode of human life, which gives the appearance of approaching some essential singularity in the history of the race beyond which human affairs, as we know them, could not continue." This concept was later fleshed out in the 1970 book Future Shock by Alvin Toffler.
Defense work

Manhattan Project
Beginning in the late 1930s, von Neumann developed an expertise in explosions—phenomena that are difficult to model mathematically. During this period, he was the leading authority of the mathematics of shaped charges, leading him to a large number of military consultancies and consequently his involvement in the Manhattan Project. The involvement included frequent trips to the project's secret research facilities at the Los Alamos Laboratory in New Mexico.
Von Neumann made his principal contribution to the atomic bomb in the concept and design of the explosive lenses that were needed to compress the plutonium core of the Fat Man weapon that was later dropped on Nagasaki. While von Neumann did not originate the "implosion" concept, he was one of its most persistent proponents, encouraging its continued development against the instincts of many of his colleagues, who felt such a design to be unworkable. He also eventually came up with the idea of using more powerful shaped charges and less fissionable material to greatly increase the speed of "assembly".
When it turned out that there would not be enough uranium-235 to make more than one bomb, the implosive lens project was greatly expanded and von Neumann's idea was implemented. Implosion was the only method that could be used with the plutonium-239 that was available from the Hanford Site. He established the design of the explosive lenses required, but there remained concerns about "edge effects" and imperfections in the explosives. His calculations showed that implosion would work if it did not depart by more than 5% from spherical symmetry. After a series of failed attempts with models, this was achieved by George Kistiakowsky, and the construction of the Trinity bomb was completed in July 1945.
In a visit to Los Alamos in September 1944, von Neumann showed that the pressure increase from explosion shock wave reflection from solid objects was greater than previously believed if the angle of incidence of the shock wave was between 90° and some limiting angle. As a result, it was determined that the effectiveness of an atomic bomb would be enhanced with detonation some kilometers above the target, rather than at ground level.

Von Neumann was included in the target selection committee that was responsible for choosing the Japanese cities of Hiroshima and Nagasaki as the first targets of the atomic bomb. Von Neumann oversaw computations related to the expected size of the bomb blasts, estimated death tolls, and the distance above the ground at which the bombs should be detonated for optimum shock wave propagation. The cultural capital Kyoto was von Neumann's first choice, a selection seconded by Manhattan Project leader General Leslie Groves. However, this target was dismissed by Secretary of War Henry L. Stimson.
On July 16, 1945, von Neumann and numerous other Manhattan Project personnel were eyewitnesses to the first test of an atomic bomb detonation, which was code-named Trinity. The event was conducted as a test of the implosion method device, at the Alamogordo Bombing Range in New Mexico. Based on his observation alone, von Neumann estimated the test had resulted in a blast equivalent to 5 kilotons of TNT (21 TJ) but Enrico Fermi produced a more accurate estimate of 10 kilotons by dropping scraps of torn-up paper as the shock wave passed his location and watching how far they scattered. The actual power of the explosion had been between 20 and 22 kilotons. It was in von Neumann's 1944 papers that the expression "kilotons" appeared for the first time.
Von Neumann continued unperturbed in his work and became, along with Edward Teller, one of those who sustained the hydrogen bomb project. He collaborated with Klaus Fuchs on further development of the bomb, and in 1946 the two filed a secret patent outlining a scheme for using a fission bomb to compress fusion fuel to initiate nuclear fusion. The Fuchs–von Neumann patent used radiation implosion, but not in the same way as is used in what became the final hydrogen bomb design, the Teller–Ulam design. Their work was, however, incorporated into the "George" shot of Operation Greenhouse, which was instructive in testing out concepts that went into the final design. The Fuchs–von Neumann work was passed on to the Soviet Union by Fuchs as part of his nuclear espionage, but it was not used in the Soviets' own, independent development of the Teller–Ulam design. The historian Jeremy Bernstein has pointed out that ironically, "John von Neumann and Klaus Fuchs, produced a brilliant invention in 1946 that could have changed the whole course of the development of the hydrogen bomb, but was not fully understood until after the bomb had been successfully made."
For his wartime services, von Neumann was awarded the Navy Distinguished Civilian Service Award in July 1946, and the Medal for Merit in October 1946.
Post-war work
In 1950, von Neumann became a consultant to the Weapons Systems Evaluation Group, whose function was to advise the Joint Chiefs of Staff and the United States Secretary of Defense on the development and use of new technologies. He also became an adviser to the Armed Forces Special Weapons Project, which was responsible for the military aspects on nuclear weapons. Over the following two years, he became a consultant across the US government. This included the Central Intelligence Agency (CIA), a member of the influential General Advisory Committee of the Atomic Energy Commission, a consultant to the newly established Lawrence Livermore National Laboratory, and a member of the Scientific Advisory Group of the United States Air Force During this time he became a "superstar" defense scientist at the Pentagon. His authority was considered infallible at the highest levels of the US government and military.
During several meetings of the advisory board of the US Air Force, von Neumann and Edward Teller predicted that by 1960 the US would be able to build a hydrogen bomb light enough to fit on top of a rocket. In 1953 Bernard Schriever, who was present at the meeting, paid a personal visit to von Neumann at Princeton to confirm this possibility. Schriever enlisted Trevor Gardner, who in turn visited von Neumann several weeks later to fully understand the future possibilities before beginning his campaign for such a weapon in Washington. Now either chairing or serving on several boards dealing with strategic missiles and nuclear weaponry, von Neumann was able to inject several crucial arguments regarding potential Soviet advancements in both these areas and in strategic defenses against American bombers into government reports to argue for the creation of ICBMs. Gardner on several occasions brought von Neumann to meetings with the US Department of Defense to discuss with various senior officials his reports. Several design decisions in these reports such as inertial guidance mechanisms would form the basis for all ICBMs thereafter. By 1954, von Neumann was also regularly testifying to various Congressional military subcommittees to ensure continued support for the ICBM program.
However, this was not enough. To have the ICBM program run at full throttle they needed direct action by the President of the United States. They convinced President Eisenhower in a direct meeting in July 1955, which resulted in a presidential directive on September 13, 1955. It stated that "there would be the gravest repercussions on the national security and on the cohesion of the free world" if the Soviet Union developed the ICBM before the US and therefore designated the ICBM project "a research and development program of the highest priority above all others." The Secretary of Defense was ordered to commence the project with "maximum urgency". Evidence would later show that the Soviets indeed were already testing their own intermediate-range ballistic missiles at the time. Von Neumann would continue to meet the President, including at his home in Gettysburg, Pennsylvania, and other high-level government officials as a key advisor on ICBMs until his death.
Atomic Energy Commission
In 1955, von Neumann became a commissioner of the Atomic Energy Commission (AEC), which at the time was the highest official position available to scientists in the government. (While his appointment formally required that he sever all his other consulting contracts, an exemption was made for von Neumann to continue working with several critical military committees after the Air Force and several key senators raised concerns.) He used this position to further the production of compact hydrogen bombs suitable for intercontinental ballistic missile (ICBM) delivery. He involved himself in correcting the severe shortage of tritium and lithium 6 needed for these weapons, and he argued against settling for the intermediate-range missiles that the Army wanted. He was adamant that H-bombs delivered deep into enemy territory by an ICBM would be the most effective weapon possible, and that the relative inaccuracy of the missile would not be a problem with an H-bomb. He said the Russians would probably be building a similar weapon system, which turned out to be the case. While Lewis Strauss was away in the second half of 1955 von Neumann took over as acting chairman of the commission.
In his final years before his death from cancer, von Neumann headed the United States government's top-secret ICBM committee, which would sometimes meet in his home. Its purpose was to decide on the feasibility of building an ICBM large enough to carry a thermonuclear weapon. Von Neumann had long argued that while the technical obstacles were sizable, they could be overcome. The SM-65 Atlas passed its first fully functional test in 1959, two years after his death. The more advanced Titan rockets were deployed in 1962. Both had been proposed in the ICBM committees von Neumann chaired. The feasibility of the ICBMs owed as much to improved, smaller warheads that did not have guidance or heat resistance issues as it did to developments in rocketry, and his understanding of the former made his advice invaluable.
Von Neumann entered government service primarily because he felt that, if freedom and civilization were to survive, it would have to be because the United States would triumph over totalitarianism from Nazism, Fascism and Soviet Communism. During a Senate committee hearing he described his political ideology as "violently anti-communist, and much more militaristic than the norm".
Personality
Work habits
Herman Goldstine commented on von Neumann's ability to intuit hidden errors and remember old material perfectly. When he had difficulties he would not labor on; instead, he would go home and sleep on it and come back later with a solution. This style, 'taking the path of least resistance', sometimes meant that he could go off on tangents. It also meant that if the difficulty was great from the very beginning, he would simply switch to another problem, not trying to find weak spots from which he could break through. At times he could be ignorant of the standard mathematical literature, finding it easier to rederive basic information he needed rather than chase references.
After World War II began, he became extremely busy with both academic and military commitments. His habit of not writing up talks or publishing results worsened. He did not find it easy to discuss a topic formally in writing unless it was already mature in his mind; if it was not, he would, in his own words, "develop the worst traits of pedantism and inefficiency".
Mathematical range
The mathematician Jean Dieudonné said that von Neumann "may have been the last representative of a once-flourishing and numerous group, the great mathematicians who were equally at home in pure and applied mathematics and who throughout their careers maintained a steady production in both directions". According to Dieudonné, his specific genius was in analysis and "combinatorics", with combinatorics being understood in a very wide sense that described his ability to organize and axiomize complex works that previously seemed to have little connection with mathematics. His style in analysis followed the German school, based on foundations in linear algebra and general topology. While von Neumann had an encyclopedic background, his range in pure mathematics was not as wide as Poincaré, Hilbert or even Weyl: von Neumann never did significant work in number theory, algebraic topology, algebraic geometry or differential geometry. However, in applied mathematics his work equalled that of Gauss, Cauchy or Poincaré.
According to Wigner, "Nobody knows all science, not even von Neumann did. But as for mathematics, he contributed to every part of it except number theory and topology. That is, I think, something unique." Halmos noted that while von Neumann knew lots of mathematics, the most notable gaps were in algebraic topology and number theory; he recalled an incident where von Neumann failed to recognize the topological definition of a torus. Von Neumann admitted to Herman Goldstine that he had no facility at all in topology and he was never comfortable with it, with Goldstine later bringing this up when comparing him to Hermann Weyl, who he thought was deeper and broader.
In his biography of von Neumann, Salomon Bochner wrote that much of von Neumann's works in pure mathematics involved finite and infinite dimensional vector spaces, which at the time, covered much of the total area of mathematics. However he pointed out this still did not cover an important part of the mathematical landscape, in particular, anything that involved geometry "in the global sense", topics such as topology, differential geometry and harmonic integrals, algebraic geometry and other such fields. Von Neumann rarely worked in these fields and, as Bochner saw it, had little affinity for them.
In one of von Neumann's last articles, he lamented that pure mathematicians could no longer attain deep knowledge of even a fraction of the field. In the early 1940s, Ulam had concocted for him a doctoral-style examination to find weaknesses in his knowledge; von Neumann was unable to answer satisfactorily a question each in differential geometry, number theory, and algebra. They concluded that doctoral exams might have "little permanent meaning". However, when Weyl turned down an offer to write a history of mathematics of the 20th century, arguing that no one person could do it, Ulam thought von Neumann could have aspired to do so.
Preferred problem-solving techniques
Ulam remarked that most mathematicians could master one technique that they then used repeatedly, whereas von Neumann had mastered three:
- A facility with the symbolic manipulation of linear operators;
- An intuitive feeling for the logical structure of any new mathematical theory;
- An intuitive feeling for the combinatorial superstructure of new theories.
Although he was commonly described as an analyst, he once classified himself an algebraist, and his style often displayed a mix of algebraic technique and set-theoretical intuition. He loved obsessive detail and had no issues with excess repetition or overly explicit notation. An example of this was a paper of his on rings of operators, where he extended the normal functional notation, to . However, this process ended up being repeated several times, where the final result were equations such as . The 1936 paper became known to students as "von Neumann's onion" because the equations "needed to be peeled before they could be digested". Overall, although his writings were clear and powerful, they were not clean or elegant. Although powerful technically, his primary concern was more with the clear and viable formation of fundamental issues and questions of science rather than just the solution of mathematical puzzles.
According to Ulam, von Neumann surprised physicists by doing dimensional estimates and algebraic computations in his head with fluency Ulam likened to blindfold chess. His impression was that von Neumann analyzed physical situations by abstract logical deduction rather than concrete visualization.
Lecture style
Goldstine compared his lectures to being on glass, smooth and lucid. By comparison, Goldstine thought his scientific articles were written in a much harsher manner, and with much less insight. Halmos described his lectures as "dazzling", with his speech clear, rapid, precise and all encompassing. Like Goldstine, he also described how everything seemed "so easy and natural" in lectures but puzzling on later reflection. He was a quick speaker: Banesh Hoffmann found it very difficult to take notes, even in shorthand, and Albert Tucker said that people often had to ask von Neumann questions to slow him down so they could think through the ideas he was presenting. Von Neumann knew about this and was grateful for his audience telling him when he was going too quickly. Although he did spend time preparing for lectures, he rarely used notes, instead jotting down points of what he would discuss and for how long.
Eidetic memory
Von Neumann was also noted for his eidetic memory, particularly of the symbolic kind. Herman Goldstine writes:
One of his remarkable abilities was his power of absolute recall. As far as I could tell, von Neumann was able on once reading a book or article to quote it back verbatim; moreover, he could do it years later without hesitation. He could also translate it at no diminution in speed from its original language into English. On one occasion I tested his ability by asking him to tell me how A Tale of Two Cities started. Whereupon, without any pause, he immediately began to recite the first chapter and continued until asked to stop after about ten or fifteen minutes.
Von Neumann was reportedly able to memorize the pages of telephone directories. He entertained friends by asking them to randomly call out page numbers; he then recited the names, addresses and numbers therein. Stanisław Ulam believed that von Neumann's memory was auditory rather than visual.
Mathematical quickness
Von Neumann's mathematical fluency, calculation speed, and general problem-solving ability were widely noted by his peers. Paul Halmos called his speed "awe-inspiring." Lothar Wolfgang Nordheim described him as the "fastest mind I ever met". Enrico Fermi told physicist Herbert L. Anderson: "You know, Herb, Johnny can do calculations in his head ten times as fast as I can! And I can do them ten times as fast as you can, Herb, so you can see how impressive Johnny is!" Edward Teller admitted that he "never could keep up with him", and Israel Halperin described trying to keep up as like riding a "tricycle chasing a racing car."
He had an unusual ability to solve novel problems quickly. George Pólya, whose lectures at ETH Zürich von Neumann attended as a student, said, "Johnny was the only student I was ever afraid of. If in the course of a lecture I stated an unsolved problem, the chances were he'd come to me at the end of the lecture with the complete solution scribbled on a slip of paper." When George Dantzig brought von Neumann an unsolved problem in linear programming "as I would to an ordinary mortal", on which there had been no published literature, he was astonished when von Neumann said "Oh, that!", before offhandedly giving a lecture of over an hour, explaining how to solve the problem using the hitherto unconceived theory of duality.
A story about von Neumann's encounter with the famous fly puzzle has entered mathematical folklore. In this puzzle, two bicycles begin 20 miles apart, and each travels toward the other at 10 miles per hour until they collide; meanwhile, a fly travels continuously back and forth between the bicycles at 15 miles per hour until it is squashed in the collision. The questioner asks how far the fly traveled in total; the "trick" for a quick answer is to realize that the fly's individual transits do not matter, only that it has been traveling at 15 miles per hour for one hour. As Eugene Wigner tells it, Max Born posed the riddle to von Neumann. The other scientists to whom he had posed it had laboriously computed the distance, so when von Neumann was immediately ready with the correct answer of 15 miles, Born observed that he must have guessed the trick. "What trick?" von Neumann replied. "All I did was sum the geometric series."
Self-doubts
Rota wrote that von Neumann had "deep-seated and recurring self-doubts". John L. Kelley reminisced in 1989 that "Johnny von Neumann has said that he will be forgotten while Kurt Gödel is remembered with Pythagoras, but the rest of us viewed Johnny with awe." Ulam suggests that some of his self-doubts with regard for his own creativity may have come from the fact he had not discovered several important ideas that others had, even though he was more than capable of doing so, giving the incompleteness theorems and Birkhoff's pointwise ergodic theorem as examples. Von Neumann had a virtuosity in following complicated reasoning and had supreme insights, yet he perhaps felt he did not have the gift for seemingly irrational proofs and theorems or intuitive insights. Ulam describes how during one of his stays at Princeton while von Neumann was working on rings of operators, continuous geometries and quantum logic he felt that von Neumann was not convinced of the importance of his work, and only when finding some ingenious technical trick or new approach did he take some pleasure in it. However, according to Rota, von Neumann still had an "incomparably stronger technique" compared to his friend, despite describing Ulam as the more creative mathematician.
Legacy
Accolades
Nobel Laureate Hans Bethe said "I have sometimes wondered whether a brain like von Neumann's does not indicate a species superior to that of man". Edward Teller observed "von Neumann would carry on a conversation with my 3-year-old son, and the two of them would talk as equals, and I sometimes wondered if he used the same principle when he talked to the rest of us." Peter Lax wrote "Von Neumann was addicted to thinking, and in particular to thinking about mathematics". Eugene Wigner said, "He understood mathematical problems not only in their initial aspect, but in their full complexity." Claude Shannon called him "the smartest person I've ever met", a common opinion. Jacob Bronowski wrote "He was the cleverest man I ever knew, without exception. He was a genius." Due to his wide reaching influence and contributions to many fields, von Neumann is widely considered a polymath.
Wigner noted the extraordinary mind that von Neumann had, and he described von Neumann as having a mind faster than anyone he knew, stating that:
I have known a great many intelligent people in my life. I knew Max Planck, Max von Laue, and Werner Heisenberg. Paul Dirac was my brother-in-law; Leo Szilard and Edward Teller have been among my closest friends; and Albert Einstein was a good friend, too. And I have known many of the brightest younger scientists. But none of them had a mind as quick and acute as Jancsi von Neumann. I have often remarked this in the presence of those men, and no one ever disputed me.
"It seems fair to say that if the influence of a scientist is interpreted broadly enough to include impact on fields beyond science proper, then John von Neumann was probably the most influential mathematician who ever lived," wrote Miklós Rédei. Peter Lax commented that von Neumann would have won a Nobel Prize in Economics had he lived longer, and that "if there were Nobel Prizes in computer science and mathematics, he would have been honored by these, too." Rota writes that "he was the first to have a vision of the boundless possibilities of computing, and he had the resolve to gather the considerable intellectual and engineering resources that led to the construction of the first large computer" and consequently that "No other mathematician in this century has had as deep and lasting an influence on the course of civilization." He is widely regarded as one of the greatest and most influential mathematicians and scientists of the 20th century.
Neurophysiologist Leon Harmon described him in a similar manner, calling him the only "true genius" he had ever met: "von Neumann's mind was all-encompassing. He could solve problems in any domain. ... And his mind was always working, always restless." While consulting for non-academic projects von Neumann's combination of outstanding scientific ability and practicality gave him a high credibility with military officers, engineers, and industrialists that no other scientist could match. In nuclear missilery he was considered "the clearly dominant advisory figure" according to Herbert York. Economist Nicholas Kaldor said he was "unquestionably the nearest thing to a genius I have ever encountered." Likewise, Paul Samuelson wrote, "We economists are grateful for von Neumann's genius. It is not for us to calculate whether he was a Gauss, or a Poincaré, or a Hilbert. He was the incomparable Johnny von Neumann. He darted briefly into our domain and it has never been the same since."
Honors and awards
Main articles: List of things named after John von Neumann and List of awards and honors received by John von Neumann
Events and awards named in recognition of von Neumann include the annual John von Neumann Theory Prize of the Institute for Operations Research and the Management Sciences, IEEE John von Neumann Medal, and the John von Neumann Prize of the Society for Industrial and Applied Mathematics. Both the crater von Neumann on the Moon and the asteroid 22824 von Neumann are named in his honor.
Von Neumann received awards including the Medal for Merit in 1947, the Medal of Freedom in 1956, and the Enrico Fermi Award also in 1956. He was elected a member of multiple honorary societies, including the American Academy of Arts and Sciences and the National Academy of Sciences, and he held eight honorary doctorates. On May 4, 2005, the United States Postal Service issued the American Scientists commemorative postage stamp series, designed by artist Victor Stabin. The scientists depicted were von Neumann, Barbara McClintock, Josiah Willard Gibbs, and Richard Feynman.
John von Neumann University [hu] was established in Kecskemét, Hungary in 2016, as a successor to Kecskemét College.
Selected works
Main article: List of scientific publications by John von NeumannVon Neumann's first published paper was On the position of zeroes of certain minimum polynomials, co-authored with Michael Fekete and published when von Neumann was 18. At 19, his solo paper On the introduction of transfinite numbers was published. He expanded his second solo paper, An axiomatization of set theory, to create his PhD thesis. His first book, Mathematical Foundations of Quantum Mechanics, was published in 1932. Following this, von Neumann switched from publishing in German to publishing in English, and his publications became more selective and expanded beyond pure mathematics. His 1942 Theory of Detonation Waves contributed to military research, his work on computing began with the unpublished 1946 On the principles of large scale computing machines, and his publications on weather prediction began with the 1950 Numerical integration of the barotropic vorticity equation. Alongside his later papers were informal essays targeted at colleagues and the general public, such as his 1947 The Mathematician, described as a "farewell to pure mathematics", and his 1955 Can we survive technology?, which considered a bleak future including nuclear warfare and deliberate climate change. His complete works have been compiled into a six-volume set.
See also
- List of pioneers in computer science
- Teapot Committee
- The MANIAC, 2023 book about von Neumann
- German: Abenteuer eines Mathematikers (English title: Adventures of a Mathematician), biopic about Stanislaw Ulam also features John von Neumann.
Notes
- Dyson 2012, p. 48.
- Israel, Giorgio ; Gasca, Ana Millan (2009). The World as a Mathematical Game: John von Neumann and Twentieth Century Science. Science Networks. Historical Studies. Vol. 38. Basel: Birkhäuser. p. 14. doi:10.1007/978-3-7643-9896-5. ISBN 978-3-7643-9896-5. OCLC 318641638.
- Goldstine 1980, p. 169.
- ^ Halperin, Israel. "The Extraordinary Inspiration of John von Neumann". In Glimm, Impagliazzo & Singer (1990), p. 16.
- While Israel Halperin's thesis advisor is often listed as Salomon Bochner, this may be because "Professors at the university direct doctoral theses but those at the Institute do not. Unaware of this, in 1934 I asked von Neumann if he would direct my doctoral thesis. He replied Yes."
- John von Neumann at the Mathematics Genealogy Project. Retrieved 2015-03-17.
- Szanton 1992, p. 130.
- Dempster, M. A. H. (February 2011). "Benoit B. Mandelbrot (1924–2010): a father of Quantitative Finance" (PDF). Quantitative Finance. 11 (2): 155–156. doi:10.1080/14697688.2011.552332. S2CID 154802171.
- Rédei 1999, p. 7.
- Macrae 1992.
- Aspray 1990, p. 246.
- Sheehan 2010.
- Doran, Robert S.; Kadison, Richard V., eds. (2004). Operator Algebras, Quantization, and Noncommutative Geometry: A Centennial Celebration Honoring John von Neumann and Marshall H. Stone. Washington, D.C.: American Mathematical Society. p. 1. ISBN 978-0-8218-3402-2.
- Myhrvold, Nathan (March 21, 1999). "John von Neumann". Time. Archived from the original on 2001-02-11.
- Blair 1957, p. 104.
- Bhattacharya 2022, p. 4.
- Dyson 1998, p. xxi.
- Macrae 1992, pp. 38–42.
- Macrae 1992, pp. 37–38.
- Macrae 1992, p. 39.
- Macrae 1992, pp. 44–45.
- "Neumann de Margitta Miksa a Magyar Jelzálog-Hitelbank igazgatója n:Kann Margit gy:János-Lajos, Mihály-József, Miklós-Ágost | Libri Regii | Hungaricana". archives.hungaricana.hu (in Hungarian). Retrieved 2022-08-08.
- ^ Macrae 1992, pp. 57–58.
- Henderson, Harry (2007). Mathematics: Powerful Patterns Into Nature and Society. New York: Chelsea House. p. 30. ISBN 978-0-8160-5750-4. OCLC 840438801.
- Schneider, Gersting & Brinkman 2015, p. 28.
- Mitchell, Melanie (2009). Complexity: A Guided Tour. Oxford University Press. p. 124. ISBN 978-0-19-512441-5. OCLC 216938473.
- Macrae 1992, pp. 46–47.
- ^ Halmos 1973, p. 383.
- ^ Blair 1957, p. 90.
- Macrae 1992, p. 52.
- Aspray 1990.
- ^ Macrae 1992, pp. 70–71.
- Impagliazzo, John; Glimm, James; Singer, Isadore Manuel The Legacy of John von Neumann, American Mathematical Society, 1990, p. 5, ISBN 0-8218-4219-6.
- Nasar, Sylvia (2001). A Beautiful Mind : a Biography of John Forbes Nash, Jr., Winner of the Nobel Prize in Economics, 1994. London: Simon & Schuster. p. 81. ISBN 978-0-7432-2457-4.
- Macrae 1992, p. 84.
- von Kármán, T., & Edson, L. (1967). The wind and beyond. Little, Brown & Company.
- Macrae 1992, pp. 85–87.
- Macrae 1992, p. 97.
- ^ Regis, Ed (November 8, 1992). "Johnny Jiggles the Planet". The New York Times. Retrieved 2008-02-04.
- von Neumann, J. (1928). "Die Axiomatisierung der Mengenlehre". Mathematische Zeitschrift (in German). 27 (1): 669–752. doi:10.1007/BF01171122. ISSN 0025-5874. S2CID 123492324.
- Macrae 1992, pp. 86–87.
- Wigner, Eugene (2001). "John von Neumann (1903–1957)". In Mehra, Jagdish (ed.). The Collected Works of Eugene Paul Wigner: Historical, Philosophical, and Socio-Political Papers. Historical and Biographical Reflections and Syntheses. Berlin: Springer. p. 128. doi:10.1007/978-3-662-07791-7. ISBN 978-3-662-07791-7.
- Pais 2000, p. 187.
- Macrae 1992, pp. 98–99.
- Weyl, Hermann (2012). Pesic, Peter (ed.). Levels of Infinity: Selected Writings on Mathematics and Philosophy (1 ed.). Dover Publications. p. 55. ISBN 978-0-486-48903-2.
- Hashagen, Ulf (2010). "Die Habilitation von John von Neumann an der Friedrich-Wilhelms-Universität in Berlin: Urteile über einen ungarisch-jüdischen Mathematiker in Deutschland im Jahr 1927". Historia Mathematica. 37 (2): 242–280. doi:10.1016/j.hm.2009.04.002.
- Dimand, Mary Ann; Dimand, Robert (2002). A History of Game Theory: From the Beginnings to 1945. London: Routledge. p. 129. ISBN 9781138006607.
- Macrae 1992, p. 145.
- Macrae 1992, pp. 143–144.
- ^ Macrae 1992, pp. 155–157.
- ^ Bochner 1958, p. 446.
- "Marina Whitman". The Gerald R. Ford School of Public Policy at the University of Michigan. July 18, 2014. Retrieved 2015-01-05.
- "Princeton Professor Divorced by Wife Here". Nevada State Journal. November 3, 1937.
- Heims 1980, p. 178.
- Macrae 1992, pp. 170–174.
- Macrae 1992, pp. 167–168.
- Macrae 1992, pp. 195–196.
- Macrae 1992, pp. 190–195.
- Macrae 1992, pp. 170–171.
- Regis, Ed (1987). Who Got Einstein's Office?: Eccentricity and Genius at the Institute for Advanced Study. Reading, Massachusetts: Addison-Wesley. p. 103. ISBN 978-0-201-12065-3. OCLC 15548856.
- ^ "Conversation with Marina Whitman". Gray Watson (256.com). Archived from the original on 2011-04-28. Retrieved 2011-01-30.
- Macrae 1992, p. 48.
- ^ Blair 1957, p. 94.
- Eisenhart, Churchill (1984). "Interview Transcript #9 - Oral History Project" (PDF) (Interview). Interviewed by William Apsray. New Jersey: Princeton Mathematics Department. p. 7. Retrieved 2022-04-03.
- ^ Goldstine 1985, p. 7.
- DeGroot, Morris H. (1989). "A Conversation with David Blackwell". In Duren, Peter (ed.). A Century of Mathematics in America: Part III. American Mathematical Society. p. 592. ISBN 0-8218-0136-8.
- Szanton 1992, p. 227.
- von Neumann Whitman, Marina. "John von Neumann: A Personal View". In Glimm, Impagliazzo & Singer (1990), p. 2.
- York 1971, p. 18.
- Pais 2006, p. 108.
- Ulam 1976, pp. 231–232.
- Ulam 1958, pp. 5–6.
- Szanton 1992, p. 277.
- Blair 1957, p. 93.
- Ulam 1976, pp. 97, 102, 244–245.
- Rota, Gian-Carlo (1989). "The Lost Cafe". In Cooper, Necia Grant; Eckhardt, Roger; Shera, Nancy (eds.). From Cardinals To Chaos: Reflections On The Life And Legacy Of Stanisław Ulam. Cambridge University Press. pp. 23–32. ISBN 978-0-521-36734-9. OCLC 18290810.
- Macrae 1992, p. 75.
- Ulam 1958, pp. 4–6.
- While Macrae gives the origin as pancreatic, the Life magazine article says it was the prostate. Sheehan's book gives it as testicular.
- Veisdal, Jørgen (November 11, 2019). "The Unparalleled Genius of John von Neumann". Medium. Retrieved 2019-11-19.
- Jacobsen 2015, p. 62.
- Poundstone, William (1993). Prisoner's Dilemma: John Von Neumann, Game Theory, and the Puzzle of the Bomb. Random House Digital. p. 194. ISBN 978-0-385-41580-4.
- Halmos 1973, pp. 383, 394.
- Jacobsen 2015, p. 63.
- Read, Colin (2012). The Portfolio Theorists: von Neumann, Savage, Arrow and Markowitz. Great Minds in Finance. Palgrave Macmillan. p. 65. ISBN 978-0230274143. Retrieved 2017-09-29.
When von Neumann realised he was incurably ill his logic forced him to realise that he would cease to exist... fate which appeared to him unavoidable but unacceptable.
- Macrae 1992, p. 379"
- Ayoub, Raymond George (2004). Musings Of The Masters: An Anthology Of Mathematical Reflections. Washington, D.C.: MAA. p. 170. ISBN 978-0-88385-549-2. OCLC 56537093.
- Macrae 1992, p. 380.
- "Nassau Presbyterian Church".
- Macrae 1992, pp. 104–105.
- ^ Van Heijenoort, Jean (1967). From Frege to Gödel: a Source Book in Mathematical Logic, 1879–1931. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-32450-3. OCLC 523838.
- Murawski 2010, p. 196.
- von Neumann, J. (1929), "Zur allgemeinen Theorie des Masses" [On the general theory of mass] (PDF), Fundamenta Mathematicae (in German), 13: 73–116, doi:10.4064/fm-13-1-73-116
- Ulam 1958, pp. 14–15.
- Von Plato, Jan (2018). "The Development of Proof Theory". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 ed.). Stanford University. Retrieved 2023-09-25.
- van der Waerden, B. L. (1975). "On the sources of my book Moderne algebra". Historia Mathematica. 2 (1): 31–40. doi:10.1016/0315-0860(75)90034-8.
- Neumann, J. v. (1927). "Zur Hilbertschen Beweistheorie". Mathematische Zeitschrift (in German). 24: 1–46. doi:10.1007/BF01475439. S2CID 122617390.
- Murawski 2010, pp. 204–206.
- ^ Rédei 2005, p. 123.
- von Plato 2018, p. 4080.
- Dawson, John W. Jr. (1997). Logical Dilemmas: The Life and Work of Kurt Gödel. Wellesley, Massachusetts: A. K. Peters. p. 70. ISBN 978-1-56881-256-4.
- von Plato 2018, pp. 4083–4088.
- von Plato 2020, pp. 24–28.
- Rédei 2005, p. 124.
- von Plato 2020, p. 22.
- Sieg, Wilfried (2013). Hilbert's Programs and Beyond. Oxford University Press. p. 149. ISBN 978-0195372229.
- Murawski 2010, p. 209.
- Hopf, Eberhard (1939). "Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung". Leipzig Ber. Verhandl. Sächs. Akad. Wiss. (in German). 91: 261–304.
Two of the papers are:
von Neumann, John (1932). "Proof of the Quasi-ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (1): 70–82. Bibcode:1932PNAS...18...70N. doi:10.1073/pnas.18.1.70. PMC 1076162. PMID 16577432.
von Neumann, John (1932). "Physical Applications of the Ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (3): 263–266. Bibcode:1932PNAS...18..263N. doi:10.1073/pnas.18.3.263. JSTOR 86260. PMC 1076204. PMID 16587674..
- Halmos 1958, p. 93.
- Halmos 1958, p. 91.
- ^ Mackey, George W. "Von Neumann and the Early Days of Ergodic Theory". In Glimm, Impagliazzo & Singer (1990), pp. 27–30.
- Ornstein, Donald S. "Von Neumann and Ergodic Theory". In Glimm, Impagliazzo & Singer (1990), p. 39.
- Halmos 1958, p. 86.
- Halmos 1958, p. 87.
- Pietsch 2007, p. 168.
- Halmos 1958, p. 88.
- ^ Dieudonné 2008.
- Ionescu-Tulcea, Alexandra; Ionescu-Tulcea, Cassius (1969). Topics in the Theory of Lifting. Springer-Verlag Berlin Heidelberg. p. V. ISBN 978-3-642-88509-9.
- Halmos 1958, p. 89.
- Neumann, J. v. (1940). "On Rings of Operators. III". Annals of Mathematics. 41 (1): 94–161. doi:10.2307/1968823. JSTOR 1968823.
- Halmos 1958, p. 90.
- Neumann, John von (1950). Functional Operators, Volume 1: Measures and Integrals. Princeton University Press. ISBN 9780691079660.
- von Neumann, John (1999). Invariant Measures. American Mathematical Society. ISBN 978-0-8218-0912-9.
- von Neumann, John (1934). "Almost Periodic Functions in a Group. I." Transactions of the American Mathematical Society. 36 (3): 445–492. doi:10.2307/1989792. JSTOR 1989792.
- von Neumann, John; Bochner, Salomon (1935). "Almost Periodic Functions in Groups, II". Transactions of the American Mathematical Society. 37 (1): 21–50. doi:10.2307/1989694. JSTOR 1989694.
- "AMS Bôcher Prize". AMS. January 5, 2016. Retrieved 2018-01-12.
- Bochner 1958, p. 440.
- von Neumann, J. (1933). "Die Einfuhrung Analytischer Parameter in Topologischen Gruppen". Annals of Mathematics. 2 (in German). 34 (1): 170–190. doi:10.2307/1968347. JSTOR 1968347.
- v. Neumann, J. (1929). "Über die analytischen Eigenschaften von Gruppen linearer Transformationen und ihrer Darstellungen". Mathematische Zeitschrift (in German). 30 (1): 3–42. doi:10.1007/BF01187749. S2CID 122565679.
- ^ Bochner 1958, p. 441.
- Pietsch 2007, p. 11.
- Dieudonné 1981, p. 172.
- Pietsch 2007, p. 14.
- Dieudonné 1981, pp. 211, 218.
- Pietsch 2007, pp. 58, 65–66.
- ^ Steen, L. A. (April 1973). "Highlights in the History of Spectral Theory". The American Mathematical Monthly. 80 (4): 359–381, esp. 370–373. doi:10.1080/00029890.1973.11993292. JSTOR 2319079.
- Pietsch, Albrecht (2014). "Traces of operators and their history". Acta et Commentationes Universitatis Tartuensis de Mathematica. 18 (1): 51–64. doi:10.12697/ACUTM.2014.18.06.
- Lord, Sukochev & Zanin 2012, p. 1.
- Dieudonné 1981, pp. 175–176, 178–179, 181, 183.
- Pietsch 2007, p. 202.
- Kar, Purushottam; Karnick, Harish (2013). "On Translation Invariant Kernels and Screw Functions". p. 2. arXiv:1302.4343 .
- Alpay, Daniel; Levanony, David (2008). "On the Reproducing Kernel Hilbert Spaces Associated with the Fractional and Bi-Fractional Brownian Motions". Potential Analysis. 28 (2): 163–184. arXiv:0705.2863. doi:10.1007/s11118-007-9070-4. S2CID 15895847.
- Horn & Johnson 2013, p. 320.
- Horn & Johnson 2013, p. 458.
- Horn, Roger A.; Johnson, Charles R. (1991). Topics in Matrix Analysis. Cambridge University Press. p. 139. ISBN 0-521-30587-X.
- Horn & Johnson 2013, p. 335.
- Bhatia, Rajendra (1997). Matrix Analysis. Graduate Texts in Mathematics. Vol. 169. New York: Springer. p. 109. doi:10.1007/978-1-4612-0653-8. ISBN 978-1-4612-0653-8.
- Lord, Sukochev & Zanin 2021, p. 73.
- Prochnoa, Joscha; Strzelecki, Michał (2022). "Approximation, Gelfand, and Kolmogorov numbers of Schatten class embeddings". Journal of Approximation Theory. 277: 105736. arXiv:2103.13050. doi:10.1016/j.jat.2022.105736. S2CID 232335769.
- "Nuclear operator". Encyclopedia of Mathematics. Archived from the original on 2021-06-23. Retrieved 2022-08-07.
- Pietsch 2007, p. 372.
- Pietsch 2014, p. 54.
- Lord, Sukochev & Zanin 2012, p. 73.
- Lord, Sukochev & Zanin 2021, p. 26.
- Pietsch 2007, p. 272.
- Pietsch 2007, pp. 272, 338.
- Pietsch 2007, p. 140.
- Murray, Francis J. "The Rings of Operators Papers". In Glimm, Impagliazzo & Singer (1990), pp. 57–59.
- Petz, D.; Rédei, M. R. "John von Neumann And The Theory Of Operator Algebras". In Bródy & Vámos (1995), pp. 163–181.
- "Von Neumann Algebras" (PDF). Princeton University. Retrieved 2016-01-06.
- ^ Dieudonné 2008, p. 90.
- Pietsch 2007, pp. 151.
- Pietsch 2007, p. 146.
- "Direct Integrals of Hilbert Spaces and von Neumann Algebras" (PDF). University of California at Los Angeles. Archived from the original (PDF) on 2015-07-02. Retrieved 2016-01-06.
- Segal 1965.
- Kadison, Richard V. "Operator Algebras - An Overview". In Glimm, Impagliazzo & Singer (1990), pp. 65,71,74.
- Pietsch 2007, p. 148.
- Birkhoff 1958, p. 50.
- ^ Lashkhi, A. A. (1995). "General geometric lattices and projective geometry of modules". Journal of Mathematical Sciences. 74 (3): 1044–1077. doi:10.1007/BF02362832. S2CID 120897087.
- von Neumann, John (1936). "Examples of continuous geometries". Proc. Natl. Acad. Sci. USA. 22 (2): 101–108. Bibcode:1936PNAS...22..101N. doi:10.1073/pnas.22.2.101. JFM 62.0648.03. JSTOR 86391. PMC 1076713. PMID 16588050.
von Neumann, John (1998) . "Continuous geometry". Proceedings of the National Academy of Sciences of the United States of America. Princeton Landmarks in Mathematics. 22 (2). Princeton University Press: 92–100. doi:10.1073/pnas.22.2.92. ISBN 978-0-691-05893-1. MR 0120174. PMC 1076712. PMID 16588062.
von Neumann, John (1962). Taub, A. H. (ed.). Collected works. Vol. IV: Continuous geometry and other topics. Oxford: Pergamon Press. MR 0157874.
von Neumann, John (1981) . Halperin, Israel (ed.). "Continuous geometries with a transition probability". Memoirs of the American Mathematical Society. 34 (252). doi:10.1090/memo/0252. ISBN 978-0-8218-2252-4. ISSN 0065-9266. MR 0634656.
- Macrae 1992, p. 140.
- von Neumann, John (1930). "Zur Algebra der Funktionaloperationen und Theorie der normalen Operatoren". Mathematische Annalen (in German). 102 (1): 370–427. Bibcode:1930MatAn.102..685E. doi:10.1007/BF01782352. S2CID 121141866.. The original paper on von Neumann algebras.
- Birkhoff 1958, pp. 50–51.
- Birkhoff 1958, p. 51.
- Wehrung, Friedrich (2006). "Von Neumann coordinatization is not first-order". Journal of Mathematical Logic. 6 (1): 1–24. arXiv:math/0409250. doi:10.1142/S0219061306000499. S2CID 39438451.
- ^ Birkhoff 1958, p. 52.
- Goodearl, Ken R. (1979). Von Neumann Regular Rings. Pitman Publishing. p. ix. ISBN 0-273-08400-3.
- Goodearl, Ken R. (1981). "Von Neumann regular rings: connections with functional analysis". Bulletin of the American Mathematical Society. 4 (2): 125–134. doi:10.1090/S0273-0979-1981-14865-5.
- Birkhoff 1958, pp. 52–53.
- Birkhoff 1958, pp. 55–56.
- von Neumann, John (1941). "Distribution of the ratio of the mean square successive difference to the variance". Annals of Mathematical Statistics. 12 (4): 367–395. doi:10.1214/aoms/1177731677. JSTOR 2235951.
- ^ Durbin, J.; Watson, G. S. (1950). "Testing for Serial Correlation in Least Squares Regression, I". Biometrika. 37 (3–4): 409–428. doi:10.2307/2332391. JSTOR 2332391. PMID 14801065.
- Sargan, J.D.; Bhargava, Alok (1983). "Testing residuals from least squares regression for being generated by the Gaussian random walk". Econometrica. 51 (1): 153–174. doi:10.2307/1912252. JSTOR 1912252.
- Rédei, László (1959). "Neumann János munkássága az algebrában és számelméletben". Matematikai Lapok (in Hungarian). 10: 226–230.
- von Neumann, J. (1925). "Egyenletesen sürü szämsorozatok (Gleichmässig dichte Zahlenfolgen)". Mat. Fiz. Lapok. 32: 32–40.
- Carbone, Ingrid; Volcic, Aljosa (2011). "A von Neumann theorem for uniformly distributed sequences of partitions". Rend. Circ. Mat. Palermo. 60 (1–2): 83–88. arXiv:0901.2531. doi:10.1007/s12215-011-0030-x. S2CID 7270857.
- Niederreiter, Harald (1975). "Rearrangement theorems for sequences". Astérisque. 24–25: 243–261.
- von Neumann, J. (1926). "Zur Prüferschen Theorie der idealen Zahlen". Acta Szeged. 2: 193–227. JFM 52.0151.02.
- Ulam 1958, pp. 9–10.
- Narkiewicz, Wladyslaw (2004). Elementary and Analytic Theory of Algebraic Numbers. Springer Monographs in Mathematics (3rd ed.). Springer. p. 120. doi:10.1007/978-3-662-07001-7. ISBN 978-3-662-07001-7. Narkiewicz, Władysław (2018). The Story of Algebraic Numbers in the First Half of the 20th Century: From Hilbert to Tate. Springer Monographs in Mathematics. Springer. p. 144. doi:10.1007/978-3-030-03754-3. ISBN 978-3-030-03754-3.
- van Dantzig, D. (1936). "Nombres universels ou p-adiques avec une introduction sur l'algèbre topologique". Annales scientifiques de l'École Normale Supérieure (in French). 53: 282–283. doi:10.24033/asens.858.
- Warner, Seth (1993). Topological Rings. North-Hollywood. p. 428. ISBN 9780080872896.
- von Neumann, J. (1928). "Die Zerlegung eines Intervalles in abzählbar viele kongruente Teilmengen". Fundamenta Mathematicae. 11 (1): 230–238. doi:10.4064/fm-11-1-230-238. JFM 54.0096.03.
- Wagon & Tomkowicz 2016, p. 73.
- Dyson 2013, p. 156.
- Harzheim, Egbert (2008). "A Construction of Subsets of the Reals which have a Similarity Decomposition". Order. 25 (2): 79–83. doi:10.1007/s11083-008-9079-3. S2CID 45005704.
- von Neumann, J. (1928). "Ein System algebraisch unabhängiger Zahlen". Mathematische Annalen. 99: 134–141. doi:10.1007/BF01459089. JFM 54.0096.02. S2CID 119788605.
- Kuiper, F.; Popken, Jan (1962). "On the So-Called von Neumann-Numbers". Indagationes Mathematicae (Proceedings). 65: 385–390. doi:10.1016/S1385-7258(62)50037-1.
- Mycielski, Jan (1964). "Independent sets in topological algebras". Fundamenta Mathematicae. 55 (2): 139–147. doi:10.4064/fm-55-2-139-147.
- Wagon & Tomkowicz 2016, p. 114.
- von Neumann, J. (1930). "Über einen Hilfssatz der Variationsrechnung". Abhandlungen Hamburg. 8: 28–31. JFM 56.0440.04.
- Miranda, Mario (1997). "Maximum principles and minimal surfaces". Annali della Scuola Normale Superiore di Pisa - Classe di Scienze. 4, 25 (3–4): 667–681.
- Gilbarg, David; Trudinger, Neil S. (2001). Elliptic Partial Differential Equations of Second Order (2 ed.). Springer. p. 316. doi:10.1007/978-3-642-61798-0. ISBN 978-3-642-61798-0.
- Ladyzhenskaya, Olga A.; Ural'tseva, Nina N. (1968). Linear and Quasilinear Elliptic Equations. Academic Press. pp. 14, 243. ISBN 978-1483253329.
- von Neumann, J. (1929). "Zum Beweise des Minkowskischen Stazes über Linearformen". Mathematische Zeitschrift. 30: 1–2. doi:10.1007/BF01187748. JFM 55.0065.04. S2CID 123066944.
- Koksma, J. F. (1936). Diophantische Approximationen (in German). Springer. p. 15. doi:10.1007/978-3-642-65618-7. ISBN 978-3-642-65618-7.
- Ulam 1958, pp. 10, 23.
- Baez, John. "State-Observable Duality (Part 2)". The n-Category Café. Retrieved 2022-08-20.
- McCrimmon, Kevin (2004). A Taste of Jordan Algebras. Universitext. New York: Springer. p. 68. doi:10.1007/b97489. ISBN 978-0-387-21796-3.
- Rédei, Miklós (1996). "Why John von Neumann did not Like the Hilbert Space formalism of quantum mechanics (and what he liked instead)". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 27 (4): 493–510. Bibcode:1996SHPMP..27..493R. doi:10.1016/S1355-2198(96)00017-2.
- Wang, Shuzhou; Wang, Zhenhua (2021). "Operator means in JB-algebras". Reports on Mathematical Physics. 88 (3): 383. arXiv:2012.13127. Bibcode:2021RpMP...88..383W. doi:10.1016/S0034-4877(21)00087-2. S2CID 229371549.
- Landsman, Nicolaas P. (2009). "Algebraic Quantum Mechanics". In Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (eds.). Compendium of Quantum Physics: Concepts, Experiments, History and Philosophy. Springer. pp. 6–7. doi:10.1007/978-3-540-70626-7. ISBN 978-3-540-70626-7.
- Kronz, Fred; Lupher, Tracy (2021). "Quantum Theory and Mathematical Rigor". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (Winter 2021 ed.). Stanford University. Retrieved 2022-12-21.
- ^ Van Hove, Léon (1958). "Von Neumann's Contributions to Quantum Theory". Bulletin of the American Mathematical Society. 64 (3): 95–99. doi:10.1090/s0002-9904-1958-10206-2.
- ^ Macrae 1992, pp. 139–141.
- Hermann, Grete (1935). "Die naturphilosophischen Grundlagen der Quantenmechanik". Naturwissenschaften. 23 (42): 718–721. Bibcode:1935NW.....23..718H. doi:10.1007/BF01491142. S2CID 40898258. English translation in Hermann, Grete (2016). Crull, Elise; Bacciagaluppi, Guido (eds.). Grete Hermann — Between physics and philosophy. Springer. pp. 239–278.
- Bell, John S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/RevModPhys.38.447. OSTI 1444158.
- Bub, Jeffrey (2010). "Von Neumann's 'No Hidden Variables' Proof: A Re-Appraisal". Foundations of Physics. 40 (9–10): 1333–1340. arXiv:1006.0499. Bibcode:2010FoPh...40.1333B. doi:10.1007/s10701-010-9480-9. S2CID 118595119.
- Mermin, N. David; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". Foundations of Physics. 48 (9): 1007–1020. arXiv:1805.10311. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5. S2CID 118951033.
- Peres, Asher (1992). "An experimental test for Gleason's theorem". Physics Letters A. 163 (4): 243–245. Bibcode:1992PhLA..163..243P. doi:10.1016/0375-9601(92)91005-C.
- Freire, Olival Jr. (2006). "Philosophy enters the optics laboratory: Bell's theorem and its first experimental tests (1965–1982)". Studies in History and Philosophy of Modern Physics. 37 (4): 577–616. arXiv:physics/0508180. Bibcode:2006SHPMP..37..577F. doi:10.1016/j.shpsb.2005.12.003. S2CID 13503517.
- Stacey, B. C. (2016). "Von Neumann was not a Quantum Bayesian". Philosophical Transactions of the Royal Society A. 374 (2068): 20150235. arXiv:1412.2409. Bibcode:2016RSPTA.37450235S. doi:10.1098/rsta.2015.0235. PMID 27091166. S2CID 16829387.
- Wigner, Eugene; Margenau, Henry (December 1967). "Remarks on the Mind Body Question, in Symmetries and Reflections, Scientific Essays". American Journal of Physics. 35 (12): 1169–1170. Bibcode:1967AmJPh..35.1169W. doi:10.1119/1.1973829.
- Schlosshauer, M.; Koer, J.; Zeilinger, A. (2013). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004. S2CID 55537196.
- Wightman, A. S. (1976). "Hilbert's Sixth Problem: Mathematical Treatment of the Axioms of Physics". In Browder, Felix E. (ed.). Mathematical Developments Arising from Hilbert Problems. American Mathematical Society. pp. 157–158. ISBN 978-0821814284.
- Kac, Rota & Schwartz 2008, p. 168.
- Rédei 2005, pp. 21, 151–152, 194.
- Nielsen, Michael A.; Chuang, Isaac (2001). Quantum computation and quantum information (reprinted ed.). Cambridge University Press. p. 700. ISBN 978-0-521-63503-5.
- "Alexandr S. Holevo".
- Wilde, Mark M. (2013). Quantum Information Theory. Cambridge University Press. p. 252.
- von Neumann, John (1927). "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik". Göttinger Nachrichten (in German). 1: 245–272.
- Schlüter, Michael; Sham, Lu Jeu (1982), "Density functional theory", Physics Today, 35 (2): 36–43, Bibcode:1982PhT....35b..36S, doi:10.1063/1.2914933, S2CID 126232754
- Fano, Ugo (June 1995), "Density matrices as polarization vectors", Rendiconti Lincei, 6 (2): 123–130, doi:10.1007/BF03001661, S2CID 128081459
- Hall, Brian C. (2013). "Systems and Subsystems, Multiple Particles". Quantum Theory for Mathematicians. Graduate Texts in Mathematics. Vol. 267. pp. 419–440. doi:10.1007/978-1-4614-7116-5_19. ISBN 978-1-4614-7115-8.
- Giulini, Domenico; Joos, Erich; Kiefer, Claus; Kupsch, Joachim; Stamatescu, Ion-Olimpiu; Zeh, H. Dieter (1996). Decoherence and the Appearance of a Classical World in Quantum Theory. Berlin, Heidelberg: Springer Berlin Heidelberg. ISBN 978-3-662-03263-3. OCLC 851393174.
- Bacciagaluppi, Guido (2020). "The Role of Decoherence in Quantum Mechanics". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Fall 2020 ed.). Stanford University. Retrieved 2023-09-25.
- Gabbay, Dov M.; Woods, John (2007). "The History of Quantum Logic". The Many Valued and Nonmonotonic Turn in Logic. Elsevier. pp. 205–2017. ISBN 978-0-08-054939-2.
- ^ Birkhoff, Garrett; von Neumann, John (October 1936). "The Logic of Quantum Mechanics". Annals of Mathematics. 37 (4): 823–843. doi:10.2307/1968621. JSTOR 1968621.
- Putnam, Hilary (1985). Philosophical Papers. Vol. 3: Realism and Reason. Cambridge University Press. p. 263. ISBN 978-0-521-31394-0.
- Rédei 2005, pp. 30–32.
- Rédei & Stöltzner 2001, pp. 53, 153–154, 168–169.
- von Neumann, John. "The Point Source Solution". In Taub (1963), pp. 219–237.
- von Neumann, John. "Theory of Detonation Waves. Progress Report to the National Defense Research Committee Div. B, OSRD-549". In Taub (1963), pp. 205–218.
- Carlucci, Donald E.; Jacobson, Sidney S. (August 26, 2013). Ballistics: Theory and Design of Guns and Ammunition (2nd ed.). CRC Press. p. 523.
- von Neumann, J.; Richtmyer, R. D. (March 1950). "A Method for the Numerical Calculation of Hydrodynamic Shocks". Journal of Applied Physics. 21 (3): 232–237. Bibcode:1950JAP....21..232V. doi:10.1063/1.1699639.
- ^ Metropolis, Nicholas; Howlett, J.; Rota, Gian-Carlo, eds. (1980). A History of Computing in the Twentieth Century. Elsevier. pp. 24–25. doi:10.1016/C2009-0-22029-0. ISBN 978-1-4832-9668-5.
- Binney, James (1996). "The stellar-dynamical oeuvre". Journal of Astrophysics and Astronomy. 17 (3–4): 81–93. Bibcode:1996JApA...17...81B. doi:10.1007/BF02702298. S2CID 56126751.
- Benacquista, Matthew J.; Downing, Jonathan M. B. (2013). "Relativistic Binaries in Globular Clusters". Living Reviews in Relativity. 16 (1): 4. arXiv:1110.4423. Bibcode:2013LRR....16....4B. doi:10.12942/lrr-2013-4. PMC 5255893. PMID 28179843.
- Uchaikin, Vladimir V.; Zolotarev, Vladimir M. (1999). Chance and Stability: Stable Distributions and their Applications. De Gruyter. pp. xviii, 281, 424. doi:10.1515/9783110935974. ISBN 9783110631159.
- Silva, J. M.; Lima, J. A. S.; de Souza, R. E.; Del Popolo, A.; Le Delliou, Morgan; Lee, Xi-Guo (2016). "Chandrasekhar's dynamical friction and non-extensive statistics". Journal of Cosmology and Astroparticle Physics. 2016 (5): 21. arXiv:1604.02034. Bibcode:2016JCAP...05..021S. doi:10.1088/1475-7516/2016/05/021. hdl:11449/173002. S2CID 118462043.
- Taub 1963, pp. 172–176.
- Bonolis, Luisa (2017). "Stellar structure and compact objects before 1940: Towards relativistic astrophysics". The European Physical Journal H. 42 (2): 311–393, esp. pp. 351, 361. arXiv:1703.09991. Bibcode:2017EPJH...42..311B. doi:10.1140/epjh/e2017-80014-4.
- Trautman, Andrzej; Trautman, Krzysztof (1994). "Generalized pure spinors". Journal of Geometry and Physics. 15 (1): 1–22. Bibcode:1994JGP....15....1T. doi:10.1016/0393-0440(94)90045-0.
- Forstnerič, Franc (2021). "The Calabi–Yau Property of Superminimal Surfaces in Self-Dual Einstein Four-Manifolds". The Journal of Geometric Analysis. 31 (5): 4754–4780. arXiv:2004.03536. doi:10.1007/s12220-020-00455-6. S2CID 215238355.
- Segal, Irving E. "The Mathematical Implications of Fundamental Physical Principles". In Glimm, Impagliazzo & Singer (1990), pp. 162–163.
- Rickles 2020, p. 89.
- Rédei 2005, pp. 21–22.
- Rédei & Stöltzner 2001, pp. 222–224.
- Rickles 2020, pp. 202–203.
- Taub 1963, p. 177.
- ^ Kuhn, H. W.; Tucker, A. W. (1958). "John von Neumann's work in the theory of games and mathematical economics". Bull. Amer. Math. Soc. 64 (Part 2) (3): 100–122. CiteSeerX 10.1.1.320.2987. doi:10.1090/s0002-9904-1958-10209-8. MR 0096572.
- von Neumann, J (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen (in German). 100: 295–320. doi:10.1007/bf01448847. S2CID 122961988.
- Lissner, Will (March 10, 1946). "Mathematical Theory of Poker Is Applied to Business Problems; GAMING STRATEGY USED IN ECONOMICS Big Potentialities Seen Strategies Analyzed Practical Use in Games". The New York Times. ISSN 0362-4331. Retrieved 2020-07-25.
- Blume, Lawrence E. (2008). "Convexity". In Durlauf, Steven N.; Blume, Lawrence E. (eds.). The New Palgrave Dictionary of Economics (2nd ed.). New York: Palgrave Macmillan. pp. 225–226. doi:10.1057/9780230226203.0315. ISBN 978-0-333-78676-5.
- For this problem to have a unique solution, it suffices that the nonnegative matrices A and B satisfy an irreducibility condition, generalizing that of the Perron–Frobenius theorem of nonnegative matrices, which considers the (simplified) eigenvalue problem
- A − λ I q = 0,
- Morgenstern, Oskar; Thompson, Gerald L. (1976). Mathematical Theory of Expanding and Contracting Economies. Lexington Books. Lexington, Massachusetts: D. C. Heath and Company. pp. xviii, 277. ISBN 978-0-669-00089-4.
- Rockafellar, R. T. (1970). Convex analysis. Princeton University Press. pp. i, 74. ISBN 978-0-691-08069-7. OCLC 64619. Rockafellar, R. T. (1974). "Convex Algebra and Duality in Dynamic Models of production". In Loz, Josef; Loz, Maria (eds.). Mathematical Models in Economics. Proc. Sympos. and Conf. von Neumann Models, Warsaw, 1972. Amsterdam: Elsevier North-Holland Publishing and Polish Academy of Sciences. pp. 351–378. OCLC 839117596.
- Ye, Yinyu (1997). "The von Neumann growth model". Interior point algorithms: Theory and analysis. New York: Wiley. pp. 277–299. ISBN 978-0-471-17420-2. OCLC 36746523.
- ^ Dore, Chakravarty & Goodwin 1989, p. xi.
- Bruckmann, Gerhart; Weber, Wilhelm, eds. (September 21, 1971). Contributions to von Neumann's Growth Model. Proceedings of a Conference Organized by the Institute for Advanced Studies Vienna, Austria, July 6 and 7, 1970. Springer–Verlag. doi:10.1007/978-3-662-24667-2. ISBN 978-3-662-22738-1.
- Dore, Chakravarty & Goodwin 1989, p. 234.
- Macrae 1992, pp. 250–253.
- Dantzig, G. B. (1983). "Reminiscences about the origins of linear programming.". In Bachem, A.; Grötschel, M.; Korte, B. (eds.). Mathematical Programming The State of the Art: Bonn 1982. Berlin, New York: Springer-Verlag. pp. 78–86. ISBN 0387120823. OCLC 9556834.
- Dantzig, George; Thapa, Mukund N. (2003). Linear Programming : 2: Theory and Extensions. New York, NY: Springer-Verlag. ISBN 978-1-4419-3140-5.
- Goldstine 1980, pp. 167–178.
- Macrae 1992, pp. 279–283.
- "BRL's Scientific Advisory Committee, 1940". U.S. Army Research Laboratory. Retrieved 2018-01-12.
- "John W. Mauchly and the Development of the ENIAC Computer". University of Pennsylvania. Archived from the original on 2007-04-16. Retrieved 2017-01-27.
- Rédei 2005, p. 73.
- Dyson 2012, pp. 267–268, 287.
- Knuth, Donald (1998). The Art of Computer Programming: Volume 3 Sorting and Searching. Boston: Addison-Wesley. p. 159. ISBN 978-0-201-89685-5.
- Knuth, Donald E. (1987). "Von Neumann's First Computer Program". In Aspray, W.; Burks, A. (eds.). Papers of John von Neumann on computing and computer theory. Cambridge: MIT Press. pp. 89–95. ISBN 978-0-262-22030-9.
- Macrae 1992, pp. 334–335.
- ^ Von Neumann, John (1951). "Various techniques used in connection with random digits". National Bureau of Standards Applied Mathematics Series. 12: 36–38.
- von Neumann, J. "Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components". In Bródy & Vámos (1995), pp. 567–616.
- Petrovic, R.; Siljak, D. (1962). "Multiplication by means of coincidence". ACTES Proc. of 3rd Int. Analog Comp. Meeting.
- Afuso, C. (1964), Quart. Tech. Prog. Rept, Illinois: Department of Computer Science, University of Illinois at Urbana-Champaign
- Chaitin, Gregory J. (2002). Conversations with a Mathematician: Math, Art, Science and the Limits of Reason. London: Springer. p. 28. doi:10.1007/978-1-4471-0185-7. ISBN 978-1-4471-0185-7.
- Pesavento, Umberto (1995). "An implementation of von Neumann's self-reproducing machine" (PDF). Artificial Life. 2 (4): 337–354. doi:10.1162/artl.1995.2.337. PMID 8942052. Archived from the original (PDF) on 2007-06-21.
- Rocha, L.M. (2015). "Von Neumann and Natural Selection". Lecture Notes of I-585-Biologically Inspired Computing Course, Indiana University (PDF). pp. 25–27. Archived from the original (PDF) on 2015-09-07. Retrieved 2016-02-06.
- Damerow, Julia, ed. (June 14, 2010). "John von Neumann's Cellular Automata". Embryo Project Encyclopedia. Arizona State University. School of Life Sciences. Center for Biology and Society. Retrieved 2024-01-14.
- von Neumann, John (1966). A. Burks (ed.). The Theory of Self-reproducing Automata. Urbana, IL: Univ. of Illinois Press. ISBN 978-0-598-37798-2.
- "2.1 Von Neumann's Contributions". Molecularassembler.com. Retrieved 2009-09-16.
- "2.1.3 The Cellular Automaton (CA) Model of Machine Replication". Molecularassembler.com. Retrieved 2009-09-16.
- von Neumann, John (1966). Arthur W. Burks (ed.). Theory of Self-Reproducing Automata (PDF). Urbana and London: University of Illinois Press. ISBN 978-0-598-37798-2.
- Toffoli, Tommaso; Margolus, Norman (1987). Cellular Automata Machines: A New Environment for Modeling. MIT Press. p. 60..
- Gustafsson 2018, p. 91.
- Gustafsson 2018, pp. 101–102.
- Gustafsson 2018, p. 235.
- Brezinski & Wuytack 2001, p. 27.
- Brezinski & Wuytack 2001, p. 216.
- Gustafsson 2018, pp. 112–113.
- Lax, Peter D. (2005). "Interview with Peter D. Lax" (PDF) (Interview). Interviewed by Martin Raussen; Christian Skau. Oslo: Notices of the American Mathematical Society. p. 223.
- Ulam, Stanisław M. (1986). Reynolds, Mark C.; Rota, Gian-Carlo (eds.). Science, Computers, and People: From the Tree of Mathematics. Boston: Birkhäuser. p. 224. doi:10.1007/978-1-4615-9819-0. ISBN 978-1-4615-9819-0.
- Hersh, Reuben (2015). Peter Lax, Mathematician: An Illustrated Memoir. American Mathematical Society. p. 170. ISBN 978-1-4704-2043-7.
- Birkhoff, Garrett (1990). "Fluid dynamics, reactor computations, and surface representation". In Nash, Stephen G. (ed.). A history of scientific computing. Association for Computing Machinery. pp. 64–69. doi:10.1145/87252.88072. ISBN 978-0-201-50814-7.
- Edwards 2010, p. 115.
- ^ Weather Architecture By Jonathan Hill (Routledge, 2013), page 216
- Edwards 2010, pp. 117–118.
- Charney, J. G.; Fjörtoft, R.; Neumann, J. (1950). "Numerical Integration of the Barotropic Vorticity Equation". Tellus. 2 (4): 237–254. Bibcode:1950Tell....2..237C. doi:10.3402/TELLUSA.V2I4.8607.
- Gilchrist, Bruce, "Remembering Some Early Computers, 1948–1960" (PDF). Archived from the original (PDF) on 2006-12-12. Retrieved 2006-12-12., Columbia University EPIC, 2006, pp.7-9. (archived 2006) Contains some autobiographical material on Gilchrist's use of the IAS computer beginning in 1952.
- Edwards 2010, p. 126.
- Edwards 2010, p. 130.
- Intraseasonal Variability in the Atmosphere-Ocean Climate System, By William K.-M. Lau, Duane E. Waliser (Springer 2011), page V
- Edwards 2010, pp. 152–153.
- Edwards 2010, pp. 153, 161, 189–190.
- "The Carbon Dioxide Greenhouse Effect". The Discovery of Global Warming. American Institute of Physics. May 2023. Retrieved 2023-10-09.
- Macrae 1992, p. 16.
- ^ Engineering: Its Role and Function in Human Society edited by William H. Davenport, Daniel I. Rosenthal (Elsevier 2016), page 266
- ^ Macrae 1992, p. 332.
- ^ Heims 1980, pp. 236–247.
- Edwards 2010, pp. 189–191.
- The Technological Singularity by Murray Shanahan, (MIT Press, 2015), page 233
- Chalmers, David (2010). "The singularity: a philosophical analysis". Journal of Consciousness Studies. 17 (9–10): 7–65.
- Jacobsen 2015, Ch. 3.
- Hoddeson et al. 1993, pp. 130–133, 157–159.
- Hoddeson et al. 1993, pp. 239–245.
- Hoddeson et al. 1993, p. 295.
- Sublette, Carey. "Section 8.0 The First Nuclear Weapons". Nuclear Weapons Frequently Asked Questions. Retrieved 2016-01-08.
- Hoddeson et al. 1993, pp. 320–327.
- Macrae 1992, p. 209.
- Hoddeson et al. 1993, p. 184.
- Macrae 1992, pp. 242–245.
- Groves, Leslie (1962). Now it Can be Told: The Story of the Manhattan Project. New York: Harper & Row. pp. 268–276. ISBN 978-0-306-70738-4. OCLC 537684.
- Hoddeson et al. 1993, pp. 371–372.
- Macrae 1992, p. 205.
- Herken, Gregg (2002). Brotherhood of the Bomb: The Tangled Lives and Loyalties of Robert Oppenheimer, Ernest Lawrence, and Edward Teller. New York: Holt. pp. 171, 374. ISBN 978-0-8050-6589-3. OCLC 48941348.
- ^ Bernstein, Jeremy (2010). "John von Neumann and Klaus Fuchs: an Unlikely Collaboration". Physics in Perspective. 12 (1): 36–50. Bibcode:2010PhP....12...36B. doi:10.1007/s00016-009-0001-1. S2CID 121790196.
- Macrae 1992, p. 208.
- ^ Macrae 1992, pp. 350–351.
- "Weapons' Values to be Appraised". Spokane Daily Chronicle. December 15, 1948. Retrieved 2015-01-08.
- Sheehan 2010, p. 182.
- Jacobsen 2015, p. 40.
- Sheehan 2010, pp. 178–179.
- Sheehan 2010, p. 199.
- Sheehan 2010, pp. 217, 219–220.
- Sheehan 2010, p. 221.
- Sheehan 2010, p. 259.
- Sheehan 2010, pp. 273, 276–278.
- Sheehan 2010, pp. 275, 278.
- Sheehan 2010, pp. 287–299.
- Sheehan 2010, p. 311.
- ^ Aspray 1990, p. 250.
- Heims 1980, p. 275.
- Aspray 1990, pp. 244–245.
- Heims 1980, p. 276.
- Macrae 1992, pp. 367–369.
- Heims 1980, p. 282.
- ^ Macrae 1992, pp. 359–365.
- Blair 1957, p. 96.
- Pais 2006, p. 109.
- Goldstine 1985, pp. 9–10.
- Albers & Alexanderson 2008, p. 81.
- ^ Goldstine 1985, p. 16.
- Ulam 1976, p. 78.
- ^ Halmos 1973, pp. 387–388.
- ^ Lax, Peter D. "Remembering John von Neumann". In Glimm, Impagliazzo & Singer (1990), p. 6.
- Rédei & Stöltzner 2001, p. 168.
- Dyson 1998, p. 77.
- Halmos 1973, p. 389.
- Ulam 1958, p. 8.
- Ulam 1976, p. 291.
- Ulam 1976, p. 96.
- Halperin, Israel (1984). "Interview Transcript #18 - Oral History Project" (PDF) (Interview). Interviewed by Albert Tucker. Princeton Mathematics Department. p. 12. Retrieved 2022-04-04.
- Ulam 1958, p. 9.
- ^ Segal, Irving E. "The Mathematical Implications of Fundamental Physical Principles". In Glimm, Impagliazzo & Singer (1990), pp. 154–156.
- Halmos 1973, p. 388.
- Ulam 1958, p. 38.
- Hoffmann, Banesh (1984). "Interview Transcript #20 - Oral History Project" (PDF) (Interview). Interviewed by Albert Tucker. Princeton Mathematics Department. p. 4. Retrieved 2022-04-04.
- Tucker 1984, p. 4.
- Goldstine 1980, pp. 167.
- John von Neumann: Life, Work, and Legacy Institute of Advanced Study, Princeton
- Ulam 1976, pp. 147–148.
- Halmos 1973, p. 386.
- Goldstine 1980, pp. 171.
- Fermi Remembered, James W. Cronin, University of Chicago Press (2004), page 236
- Teller, Edward (April 1957). "John von Neumann". Bulletin of the Atomic Scientists. 13 (4): 150–151. Bibcode:1957BuAtS..13d.150T. doi:10.1080/00963402.1957.11457538.
- Kaplan, Michael and Kaplan, Ellen (2006) Chances are–: adventures in probability. Viking.
- Petković, Miodrag (2009). Famous puzzles of great mathematicians. American Mathematical Society. p. 157. ISBN 978-0-8218-4814-2.
- Mirowski, Philip (2002). Machine Dreams: Economics Becomes a Cyborg Science. Cambridge University Press. p. 258. ISBN 978-0-521-77283-9. OCLC 45636899.
- "Fly Puzzle (Two Trains Puzzle)". Wolfram MathWorld. February 15, 2014. Retrieved 2014-02-25.
- "John von Neumann – A Documentary". The Mathematical Association of America. 1966. 17m00s – 19m11s. Retrieved 2022-08-26.
- Halmos 1973, pp. 386–387.
- ^ Rota 1997, p. 71.
- Kelley, J. L. (1989). "Once Over Lightly". In Duren, Peter (ed.). A Century of Mathematics in America: Part III. American Mathematical Society. p. 478. ISBN 0-8218-0136-8.
- Ulam 1976, pp. 76–77.
- Nowak, Amram (January 1, 1966). "John Von Neumann a documentary". Mathematical Association of America, Committee on Educational Media. OCLC 177660043., DVD version (2013) OCLC 897933992.
- ^ Szanton 1992, p. 58.
- Soni, Jimmy; Goodman, Rob (2017). A Mind at Play: How Claude Shannon Invented the Information Age. Simon & Schuster. p. 76. ISBN 978-1476766683.
- Bronowski, Jacob (1974). The Ascent of Man. Boston: Little, Brown. p. 433.
- "John von Neumann". Atomic Heritage Foundation. Retrieved 2024-11-06.
- Robinson, Andrew (December 18, 2021). "Brilliant polymath, troubled person: how John von Neumann shaped our world". Physics World. Retrieved 2024-11-06.
- Adami, Christoph (2024). The Evolution of Biological Information: How Evolution Creates Complexity, from Viruses to Brains. Princeton: Princeton University Press. pp. 189–190. ISBN 978-0-691-24114-2.
- Rédei 2005, p. 7.
- Rédei 2005, p. xiii.
- Rota 1997, p. 70.
- Ulam 1976, p. 4; Kac, Rota & Schwartz 2008, p. 206; Albers & Alexanderson 2008, p. 168; Szanton 1992, p. 51 Rhodes, Richard (1995). Dark Sun: The Making of the Hydrogen Bomb. New York: Simon & Schuster. p. 250. ISBN 0-684-80400-X. Doedel, Eusebius J.; Domokos, Gábor; Kevrekidis, Ioannis G. (March 2006). "Modeling and Computations in Dynamical Systems". World Scientific Series on Nonlinear Science Series B. 13. doi:10.1142/5982. ISBN 978-981-256-596-9.
- McCorduck, Pamela (2004). Machines Who Think: A Personal Inquiry into the History and Prospects of Artificial Intelligence (2nd ed.). Routledge. p. 81. ISBN 978-1568812052.
- York 1971, p. 85.
- Dore, Chakravarty & Goodwin 1989, p. 121.
- "John von Neumann Theory Prize". Institute for Operations Research and the Management Sciences. Archived from the original on 2016-05-13. Retrieved 2016-05-17.
- "IEEE John von Neumann Medal". IEEE Awards. Institute of Electrical and Electronics Engineers. Retrieved 2024-07-30.
- "The John von Neumann Lecture". Society for Industrial and Applied Mathematics. Retrieved 2016-05-17.
- "Von Neumann". United States Geological Survey. Retrieved 2016-05-17.
- "22824 von Neumann (1999 RP38)". Jet Propulsion Laboratory. Retrieved 2018-02-13.
- "(22824) von Neumann = 1999 RP38 = 1998 HR2". Minor Planet Center. Retrieved 2018-02-13.
- "Dwight D. Eisenhower: Citation Accompanying Medal of Freedom Presented to Dr. John von Neumann". The American Presidency Project.
- Aspray 1990, pp. 246–247.
- Ulam 1958, pp. 41–42.
- "Von Neumann, John, 1903–1957". Physics History Network. American Institute of Physics. Retrieved 2023-10-12.
- "American Scientists Issue". Arago: People, Postage & the Post. National Postal Museum. Archived from the original on 2016-02-02. Retrieved 2022-08-02.
- "Neumann János Egyetem". Neumann János Egyetem.
- ^ Dyson 2013, p. 154.
- Dyson 2013, p. 155.
- Dyson 2013, p. 157.
- Dyson 2013, p. 158.
- Dyson 2013, p. 159.
- von Neumann, John (1947). "The Mathematician". In Heywood, Robert B. (ed.). The Works of the Mind. University of Chicago Press. OCLC 752682744.
- Dyson 2013, pp. 159–160.
References
- Albers, Donald J.; Alexanderson, Gerald L., eds. (2008). Mathematical People: Profiles and Interviews (2 ed.). CRC Press. doi:10.1201/b10585. ISBN 978-1568813400.
- Aspray, William (1990). John von Neumann and the Origins of Modern Computing. Cambridge, Massachusetts: MIT Press. Bibcode:1990jvno.book.....A. ISBN 978-0262518857. OCLC 21524368.
- Bhattacharya, Ananyo (2022). The Man from the Future: The Visionary Life of John von Neumann. W. W. Norton & Company. ISBN 978-1324003991.
- Birkhoff, Garret (1958). "Von Neumann and lattice theory". Bulletin of the American Mathematical Society. 64 (3, Part 2): 50–56. doi:10.1090/S0002-9904-1958-10192-5.
- Blair, Clay Jr. (February 25, 1957). "Passing of a Great Mind". Life. pp. 89–104.
- Bochner, S. (1958). "John von Neumann 1903–1957: A Biographical Memoir" (PDF). National Academy of Sciences. Retrieved 2025-01-16.
- Brezinski, C.; Wuytack, L. (2001). Numerical Analysis: Historical Developments in the 20th Century. Elsevier. doi:10.1016/C2009-0-10776-6. ISBN 9780444598585.
- Bródy, F.; Vámos, Tibor, eds. (1995). The Neumann Compendium. World Scientific Series in 20th Century Mathematics. Vol. 1. Singapore: World Scientific Publishing Company. doi:10.1142/2692. ISBN 978-981-02-2201-7. OCLC 32013468.
- Dieudonné, Jean (1981). History of Functional Analysis. North-Hollywood Publishing Company. ISBN 978-0444861481.
- Dieudonné, J. (2008). "Von Neumann, Johann (or John)". In Gillispie, C. C. (ed.). Complete Dictionary of Scientific Biography. Vol. 14 (7th ed.). Detroit: Charles Scribner's Sons. pp. 88–92 Gale Virtual Reference Library. ISBN 978-0-684-31559-1. OCLC 187313311.
- Dore, Mohammed; Chakravarty, Sukhamoy; Goodwin, Richard, eds. (1989). John von Neumann and Modern Economics. Oxford: Clarendon. ISBN 978-0-19-828554-0. OCLC 18520691.
- Dyson, George (1998). Darwin among the machines the evolution of global intelligence. Cambridge, Massachusetts: Perseus Books. ISBN 978-0-7382-0030-9. OCLC 757400572.
- Dyson, George (2012). Turing's Cathedral: the Origins of the Digital Universe. New York: Pantheon Books. ISBN 978-0-375-42277-5. OCLC 745979775.
"I am thinking of something much more important than bombs. I am thinking about computers"
- Dyson, Freeman (2013). "A Walk through Johnny von Neumann's Garden". Notices of the AMS. 60 (2): 154–161. doi:10.1090/noti942.
- Edwards, Paul N. (2010). A Vast Machine: Computer Models, Climate Data, and the Politics of Global Warming. The MIT Press. ISBN 978-0-262-01392-5.
- Glimm, James; Impagliazzo, John; Singer, Isadore Manuel, eds. (1990). The Legacy of John von Neumann. American Mathematical Society. ISBN 978-0-8218-4219-5.
- Goldstine, Herman (1980). The Computer from Pascal to von Neumann. Princeton University Press. ISBN 978-0-691-02367-0.
- Goldstine, Herman (1985). "Interview Transcript #15 - Oral History Project" (PDF) (Interview). Interviewed by Albert Tucker; Frederik Nebeker. Maryland: Princeton Mathematics Department. Retrieved 2022-04-03.
- Gustafsson, Bertil (2018). Scientific Computing: A Historical Perspective. Texts in Computational Science and Engineering. Vol. 17. Springer. doi:10.1007/978-3-319-69847-2. ISBN 978-3-319-69847-2.
- Halmos, Paul R. (1958). "Von Neumann on measure and ergodic theory". Bulletin of the American Mathematical Society. 64 (3, Part 2): 86–94. doi:10.1090/S0002-9904-1958-10203-7.
- Halmos, Paul (1973). "The Legend of John Von Neumann". The American Mathematical Monthly. 80 (4): 382–394. doi:10.1080/00029890.1973.11993293.
- Heims, Steve J. (1980). John von Neumann and Norbert Wiener, from Mathematics to the Technologies of Life and Death. Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-08105-4.
- Hoddeson, Lillian; Henriksen, Paul W.; Meade, Roger A.; Westfall, Catherine L. (1993). Critical Assembly: A Technical History of Los Alamos During the Oppenheimer Years, 1943–1945. New York: Cambridge University Press. ISBN 978-0-521-44132-2. OCLC 26764320.
- Horn, Roger A.; Johnson, Charles R. (2013). Matrix Analysis (2 ed.). Cambridge University Press. ISBN 978-0-521-83940-2.
- Jacobsen, Annie (2015). The Pentagon's Brain: An Uncensored History Of DARPA, America's Top Secret Military Research Agency. Little, Brown and Company. ISBN 978-0316371667. OCLC 1037806913.
- Kac, Mark; Rota, Gian-Carlo; Schwartz, Jacob T. (2008). Discrete Thoughts: Essays on Mathematics, Science and Philosophy (2 ed.). Boston: Birkhäuser. doi:10.1007/978-0-8176-4775-9. ISBN 978-0-8176-4775-9.
- Lord, Steven; Sukochev, Fedor; Zanin, Dmitriy (2012). Singular Traces: Theory and Applications (1 ed.). De Gruyter. doi:10.1515/9783110262551. ISBN 9783110262551.
- Lord, Steven; Sukochev, Fedor; Zanin, Dmitriy (2021). Singular Traces Volume 1: Theory (2 ed.). De Gruyter. doi:10.1515/9783110378054. ISBN 9783110378054. S2CID 242485577.
- Macrae, Norman (1992). John von Neumann: The Scientific Genius Who Pioneered the Modern Computer, Game Theory, Nuclear Deterrence, and Much More. Pantheon Press. ISBN 978-0-679-41308-0. Description, contents, incl. arrow-scrollable preview, & review.
- Murawski, Roman (2010). "John Von Neumann and Hilbert's School". Essays in the Philosophy and History of Logic and Mathematics. Amsterdam: Rodopi. pp. 195–209. doi:10.1163/9789042030916_015. ISBN 978-90-420-3091-6.
- Pais, Abraham (2000). The Genius of Science: A Portrait Gallery: A Portrait Gallery of Twentieth-Century Physicists. Oxford University Press. ISBN 978-0198506140.
- Pais, Abraham (2006). J. Robert Oppenheimer: A Life. Oxford: Oxford University Press. ISBN 978-0-19-516673-6. OCLC 475574884.
- Pietsch, Albrecht (2007). History of Banach Spaces and Linear Operators. Boston: Birkhäuser. doi:10.1007/978-0-8176-4596-0. ISBN 978-0-8176-4596-0.
- Rédei, Miklós (1999). "Unsolved Problems in Mathematics" (PDF). The Mathematical Intelligencer. 21: 7–12. doi:10.1007/BF03025331. S2CID 117002529.
- Rédei, Miklós; Stöltzner, Michael, eds. (2001). John von Neumann and the Foundations of Quantum Physics. Springer. doi:10.1007/978-94-017-2012-0. ISBN 978-0792368120.
- Rédei, Miklós, ed. (2005). John von Neumann: Selected Letters. History of Mathematics. Vol. 27. Providence, Rhode Island: American Mathematical Society. ISBN 978-0-8218-3776-4. OCLC 60651134.
- Rickles, Dean (2020). Covered with Deep Mist: The Development of Quantum Gravity 1916–1956. Oxford University Press. doi:10.1093/oso/9780199602957.001.0001. ISBN 9780199602957.
- Rota, Gian-Carlo (1997). Palombi, Fabrizio (ed.). Indiscrete Thoughts. Boston, MA: Birkhäuser. doi:10.1007/978-0-8176-4781-0. ISBN 978-0-8176-4781-0.
- Schneider, G. Michael; Gersting, Judith; Brinkman, Bo (2015). Invitation to Computer Science. Boston: Cengage Learning. ISBN 978-1-305-07577-1. OCLC 889643614.
- Segal, Irving (1965). "Algebraic Integration Theory". Bulletin of the American Mathematical Society. 71 (3): 419–489. doi:10.1090/S0002-9904-1965-11284-8.
- Sheehan, Neil (2010). A Fiery Peace in a Cold War: Bernard Schriever and the Ultimate Weapon. Vintage. ISBN 978-0679745495.
- Szanton, Andrew (1992). The Recollections of Eugene P. Wigner: as told to Andrew Szanton (1 ed.). Springer. doi:10.1007/978-1-4899-6313-0. ISBN 978-1-4899-6313-0.
- Taub, A. H., ed. (1963). John von Neumann Collected Works Volume VI: Theory of Games, Astrophysics, Hydrodynamics and Meteorology. New York: Pergamon Press. ISBN 978-0-08-009566-0. OCLC 493423386.
- Tucker, Albert (1984). "Interview Transcript #34 - Oral History Project" (PDF) (Interview). Interviewed by William Aspray. Princeton: Princeton Mathematics Department. Retrieved 2022-04-04.
- Ulam, Stanisław (1958). "John von Neumann 1903–1957" (PDF). Bull. Amer. Math. Soc. 64 (3): 1–49. doi:10.1090/S0002-9904-1958-10189-5.
- Ulam, Stanisław (1976). Adventures of a Mathematician. New York: Charles Scribner's Sons. ISBN 0-684-14391-7.
- von Plato, Jan (2018). "In search of the sources of incompleteness" (PDF). Proceedings of the International Congress of Mathematicians 2018. 3: 4075–4092. doi:10.1142/9789813272880_0212. ISBN 978-981-327-287-3. S2CID 203463751.
- von Plato, Jan (2020). Can Mathematics Be Proved Consistent?. Sources and Studies in the History of Mathematics and Physical Sciences. Springer International Publishing. doi:10.1007/978-3-030-50876-0. ISBN 978-3-030-50876-0. S2CID 226522427.
- Wagon, Stan; Tomkowicz, Grzegorz (2016). The Banach–Tarski Paradox (2 ed.). Cambridge University Press. ISBN 9781316572870.
- York, Herbert (1971). Race to Oblivion: A Participant's View of the Arms Race. New York: Simon and Schuster. ISBN 978-0671209315.
Further reading
Books
- Erickson, Paul (2015). The World the Game Theorists Made. University of Chicago Press. ISBN 9780226097176.
- Halmos, Paul R. (1985). I Want To Be A Mathematician: an Automathography. New York: Springer-Verlag. doi:10.1007/978-1-4612-1084-9. ISBN 978-0-387-96078-4. OCLC 11497873.
- Hargittai, Balazs; Hargittai, Istvan (2015). Wisdom of the Martians of Science: In Their Own Words with Commentaries. World Scientific. doi:10.1142/9809. ISBN 978-9814723817.
- Hargittai, Istvan (2008). Martians of Science: Five Physicists Who Changed the Twentieth Century. Oxford University Press. doi:10.1093/acprof:oso/9780195178456.001.0001. ISBN 978-0195365566.
- Horvath, Janos, ed. (2006). A Panorama of Hungarian Mathematics in the Twentieth Century I. Bolyai Society Mathematical Studies. Vol. 14. Springer. doi:10.1007/978-3-540-30721-1. ISBN 978-3540289456.
- Krehl, Peter O. K. (2009). History of Shock Waves, Explosions and Impact: A Chronological and Biographical Reference. Springer. doi:10.1007/978-3-540-30421-0. ISBN 978-3-540-30421-0.
- Leonard, Robert (2010). Von Neumann, Morgenstern, and the Creation of Game Theory: From Chess to Social Science, 1900–1960. Cambridge University Press. doi:10.1017/CBO9780511778278. ISBN 978-1107609266.
- Poundstone, William (1993). Prisoner's Dilemma: John Von Neumann, Game Theory, and the Puzzle of the Bomb. Random House Digital. ISBN 978-0-385-41580-4.
- Purrington, Robert D. (2018). The Heroic Age: The Creation of Quantum Mechanics, 1925–1940. Oxford University Press. ISBN 978-0190655174.
- Slater, Robert (1989). Portraits in Silicon. Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-19262-0. OCLC 15630421.
- von Neumann Whitman, Marina (2012). The Martian's Daughter—A Memoir. Anne Arbor: University of Michigan Press. ISBN 978-0-472-03564-9. OCLC 844308382.
- Vonneuman, Nicholas A. (1987). John von Neumann as Seen by His Brother (PDF). Meadowbrook, Pennsylvania: N.A. Vonneuman. ISBN 978-0-9619681-0-6. OCLC 17547196.
- Weintraub, E. Roy, ed. (1992). Towards a History of Game Theory. History of Political Economy. Vol. 24 (Supplement). ISSN 0018-2702.
Popular periodicals
- Grafton, Samuel (September 1956). "Married to a Man Who Believes the Mind Can Move the World". Good Housekeeping Magazine (Interview with Klari von Neumann). pp. 80–81, 282–292.
Journals
- Formica, Giambattista (2022). "John von Neumann's Discovery of the 2nd Incompleteness Theorem". History and Philosophy of Logic. 44: 66–90. doi:10.1080/01445340.2022.2137324. S2CID 256699234.
- Smithies, F. (1959). "John von Neumann". Journal of the London Mathematical Society. s1-34 (3): 373–384. doi:10.1112/jlms/s1-34.3.373.
- Carvajalino, Juan (2021). "Unlocking the Mystery of the Origins of John von Neumann's Growth Model". History of Political Economy. 53 (4): 595–631. doi:10.1215/00182702-9308883.
- Carvajalino, Juan (2022). "Where Did John von Neumann's Mathematical Economics Come From?". History of Political Economy. 54 (5): 823–858. doi:10.1215/00182702-10005718.
- Boldyrev, Ivan (2024). "The Frame for the Not-Yet Existent: How American, European, and Soviet Scholars Jointly Shaped Modern Mathematical Economics". History of Political Economy. 56 (3): 467–488. doi:10.1215/00182702-11156216.
External links
- A more or less complete bibliography of publications of John von Neumann by Nelson H. F. Beebe
- O'Connor, John J.; Robertson, Edmund F., "John von Neumann", MacTutor History of Mathematics Archive, University of St Andrews
- von Neumann's profile at Google Scholar
- Oral History Project - The Princeton Mathematics Community in the 1930s, contains many interviews that describe contact and anecdotes of von Neumann and others at the Princeton University and Institute for Advanced Study community.
- Oral history interviews (from the Charles Babbage Institute, University of Minnesota) with: Alice R. Burks and Arthur W. Burks; Eugene P. Wigner; and Nicholas C. Metropolis.
- zbMATH profile
- Query for "von neumann" on the digital repository of the Institute for Advanced Study.
- Von Neumann vs. Dirac on Quantum Theory and Mathematical Rigor – from Stanford Encyclopedia of Philosophy
- Quantum Logic and Probability Theory - from Stanford Encyclopedia of Philosophy
- FBI files on John von Neumann released via FOI
- Biographical video by David Brailsford (John Dunford Professor Emeritus of computer science at the University of Nottingham)
- John von Neumann: Prophet of the 21st Century 2013 Arte documentary on John von Neumann and his influence in the modern world (in German and French with English subtitles).
- John von Neumann - A Documentary 1966 detailed documentary by the Mathematical Association of America containing remarks by several of his colleagues including Ulam, Wigner, Halmos, Morgenstern, Bethe, Goldstine, Strauss and Teller.
| Set theory | ||
|---|---|---|
| Overview |  | |
| Axioms | ||
| Operations |
| |
| ||
| Set types | ||
| Theories | ||
| ||
| Set theorists | ||
- John von Neumann
- 1903 births
- 1957 deaths
- 20th-century American mathematicians
- 20th-century American physicists
- Algebraists
- American anti-communists
- American computer scientists
- American nuclear physicists
- American operations researchers
- American people of Hungarian-Jewish descent
- American Roman Catholics
- Hungarian physicists
- American systems scientists
- Mathematicians from Austria-Hungary
- Ballistics experts
- Burials at Princeton Cemetery
- Deaths from cancer in Washington, D.C.
- Carl-Gustaf Rossby Research Medal recipients
- Cellular automatists
- Computer designers
- Converts to Roman Catholicism from Judaism
- Cyberneticists
- Elected Members of the International Statistical Institute
- Enrico Fermi Award recipients
- ETH Zurich alumni
- Fasori Gimnázium alumni
- Fellows of the American Physical Society
- Fellows of the Econometric Society
- Fluid dynamicists
- Functional analysts
- Game theorists
- Hungarian anti-communists
- Hungarian computer scientists
- Hungarian emigrants to the United States
- 20th-century Hungarian inventors
- 20th-century Hungarian Jews
- 20th-century Hungarian mathematicians
- 20th-century Hungarian physicists
- Hungarian nobility
- Hungarian nuclear physicists
- Hungarian Roman Catholics
- Institute for Advanced Study faculty
- Jewish anti-communists
- Jewish American physicists
- Lattice theorists
- Manhattan Project people
- Mathematical economists
- Mathematical physicists
- Mathematicians from Budapest
- Measure theorists
- Medal for Merit recipients
- Members of the American Philosophical Society
- Members of the Lincean Academy
- Members of the Royal Netherlands Academy of Arts and Sciences
- Members of the United States National Academy of Sciences
- Mental calculators
- Monte Carlo methodologists
- Naturalized citizens of the United States
- Numerical analysts
- Oak Ridge National Laboratory people
- Operations researchers
- Operator theorists
- People from Pest, Hungary
- Presidents of the American Mathematical Society
- Princeton University faculty
- Probability theorists
- Quantum physicists
- RAND Corporation people
- Recipients of the Medal of Freedom
- Researchers of artificial life
- American set theorists
- Theoretical physicists
- Academic staff of the University of Göttingen
- Von Neumann family
- Yiddish-speaking people
- Academic staff of the University of Hamburg
- Recipients of the Navy Distinguished Civilian Service Award
 and states that for every vector
and states that for every vector  in the
in the  exists in the sense of the metric defined by the Hilbert norm and is a vector
exists in the sense of the metric defined by the Hilbert norm and is a vector  which is such that
which is such that  for all
for all  . This was proven in the first paper. In the second paper, von Neumann argued that his results here were sufficient for physical applications relating to
. This was proven in the first paper. In the second paper, von Neumann argued that his results here were sufficient for physical applications relating to  and proving several other results on what are now known as Schatten–von Neumann ideals.
and proving several other results on what are now known as Schatten–von Neumann ideals.
 it can be an element of the
it can be an element of the  . Earlier,
. Earlier,  (continuous-dimensional projective geometry over an arbitrary
(continuous-dimensional projective geometry over an arbitrary  ) in abstract language of lattice theory. Von Neumann provided an abstract exploration of dimension in completed
) in abstract language of lattice theory. Von Neumann provided an abstract exploration of dimension in completed  every
every  -dimensional abstract projective geometry is
-dimensional abstract projective geometry is  over a (unique) corresponding division ring
over a (unique) corresponding division ring  . This is known as the
. This is known as the  , an element
, an element  exists such that
exists such that  . These rings came from and have connections to his work on von Neumann algebras, as well as
. These rings came from and have connections to his work on von Neumann algebras, as well as  -divisible. Von Neumann proved that indeed that all intervals, half-open, open, or closed are
-divisible. Von Neumann proved that indeed that all intervals, half-open, open, or closed are 
 are algebraically independent for
are algebraically independent for  . Consequently, there exists a perfect algebraically independent set of reals the size of the
. Consequently, there exists a perfect algebraically independent set of reals the size of the  , it is given by
, it is given by  Many of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and
Many of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and  . It was also demonstrated that the laws of distribution of classical logic,
. It was also demonstrated that the laws of distribution of classical logic, 
 and
and 
 , are not valid for quantum theory.
, are not valid for quantum theory.
 along with two inequality systems expressing economic efficiency. In this model, the (
along with two inequality systems expressing economic efficiency. In this model, the ( to
to  . However, this process ended up being repeated several times, where the final result were equations such as
. However, this process ended up being repeated several times, where the final result were equations such as  . The 1936 paper became known to students as "von Neumann's onion" because the equations "needed to be peeled before they could be digested". Overall, although his writings were clear and powerful, they were not clean or elegant. Although powerful technically, his primary concern was more with the clear and viable formation of fundamental issues and questions of science rather than just the solution of mathematical puzzles.
. The 1936 paper became known to students as "von Neumann's onion" because the equations "needed to be peeled before they could be digested". Overall, although his writings were clear and powerful, they were not clean or elegant. Although powerful technically, his primary concern was more with the clear and viable formation of fundamental issues and questions of science rather than just the solution of mathematical puzzles.