The grain boundary diffusion coefficient is the diffusion coefficient of a diffusant along a grain boundary in a polycrystalline solid. It is a physical constant denoted , and it is important in understanding how grain boundaries affect atomic diffusivity. Grain boundary diffusion is a commonly observed route for solute migration in polycrystalline materials. It dominates the effective diffusion rate at lower temperatures in metals and metal alloys. Take the apparent self-diffusion coefficient for single-crystal and polycrystal silver, for example. At high temperatures, the coefficient is the same in both types of samples. However, at temperatures below 700 °C, the values of with polycrystal silver consistently lie above the values of with a single crystal.
Measurement
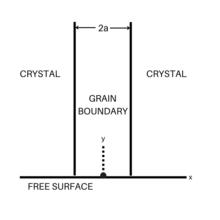
The general way to measure grain boundary diffusion coefficients was suggested by Fisher. In the Fisher model, a grain boundary is represented as a thin layer of high-diffusivity uniform and isotropic slab embedded in a low-diffusivity isotropic crystal. Suppose that the thickness of the slab is , the length is , and the depth is a unit length, the diffusion process can be described as the following formula. The first equation represents diffusion in the volume, while the second shows diffusion along the grain boundary, respectively.
where
where is the volume concentration of the diffusing atoms and is their concentration in the grain boundary.
To solve the equation, Whipple introduced an exact analytical solution. He assumed a constant surface composition, and used a Fourier–Laplace transform to obtain a solution in integral form. The diffusion profile therefore can be depicted by the following equation.
To further determine , two common methods were used. The first is used for accurate determination of . The second technique is useful for comparing the relative of different boundaries.
- Method 1: Suppose the slab was cut into a series of thin slices parallel to the sample surface, we measure the distribution of in-diffused solute in the slices, . Then we used the above formula that developed by Whipple to get .
- Method 2: To compare the length of penetration of a given concentration at the boundary with the length of lattice penetration from the surface far from the boundary.
References
- P. Heitjans, J. Karger, Ed, “Diffusion in condensed matter: Methods, Materials, Models,” 2nd edition, Birkhauser, 2005, pp. 1-965.
- Shewmon, Paul (2016). Diffusion in Solids. Bibcode:2016diso.book.....S. doi:10.1007/978-3-319-48206-4. ISBN 978-3-319-48564-5. S2CID 137442988.
- Fisher, J. C. (January 1951). "Calculation of Diffusion Penetration Curves for Surface and Grain Boundary Diffusion". Journal of Applied Physics. 22 (1): 74–77. Bibcode:1951JAP....22...74F. doi:10.1063/1.1699825. ISSN 0021-8979.
- Whipple, R.T.P. (1954-12-01). "CXXXVIII. Concentration contours in grain boundary diffusion". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 45 (371): 1225–1236. doi:10.1080/14786441208561131. ISSN 1941-5982.
 , and it is important in understanding how grain boundaries affect
, and it is important in understanding how grain boundaries affect  , where
, where  is the diffusion coefficient,
is the diffusion coefficient,  is the boundary width, and
is the boundary width, and  is the rate of sideflow.
is the rate of sideflow. , the length is
, the length is  , and the depth is a unit length, the diffusion process can be described as the following formula. The first equation represents diffusion in the volume, while the second shows diffusion along the grain boundary, respectively.
, and the depth is a unit length, the diffusion process can be described as the following formula. The first equation represents diffusion in the volume, while the second shows diffusion along the grain boundary, respectively.
 where
where 

 is the volume concentration of the diffusing atoms and
is the volume concentration of the diffusing atoms and  is their concentration in the grain boundary.
is their concentration in the grain boundary.

 . The second technique is useful for comparing the relative
. The second technique is useful for comparing the relative  . Then we used the above formula that developed by Whipple to get
. Then we used the above formula that developed by Whipple to get  with the length of lattice penetration from the surface far from the boundary.
with the length of lattice penetration from the surface far from the boundary.