
Garfield's proof of the Pythagorean theorem is an original proof the Pythagorean theorem discovered by James A. Garfield (November 19, 1831 – September 19, 1881), the 20th president of the United States. The proof appeared in print in the New-England Journal of Education (Vol. 3, No.14, April 1, 1876). At the time of the publication of the proof Garfield was not the President, he was only the Congressman from Ohio. He assumed the office of President on March 4, 1881, and served in that position only for a brief period up to September 19, 1881 when he was assassinated. Garfield was the only President of the United States to have contributed anything original to mathematics. The proof is nontrivial and, according to the historian of mathematics, William Dunham, "Garfield's is really a very clever proof." The proof appears as the 231st proof in The Pythagorean Proposition, a compendium of 370 different proofs of the Pythagorean theorem.
The proof
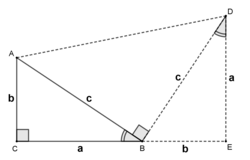
In the figure, is a right-angled triangle with right angle at . The side-lengths of the triangle are . Pythagorean theorem asserts that .
To prove the theorem, Garfield drew a line through perpendicular to and on this line chose a point such that . Then, from he dropped a perpendicular upon the extended line . From the figure, one can easily see that the triangles and are congruent. Since and are both perpendicular to , they are parallel and so the quadrilateral is a trapezoid. The theorem is proved by computing the area of this trapezoid in two different ways.
- .
From these one gets
which on simplification yields
References
- G., J. A. (1876). "PONS ASINORUM". New England Journal of Education. 3 (14): 161. ISSN 2578-4145. JSTOR 44764657.
- Sid J. Kolpas. "Mathematical Treasure: James A. Garfield's Proof of the Pythagorean Theorem". maa.org. Mathematical Association of America. Retrieved 29 November 2023. (The article appeared in the peer-reviewed online journal Convergence published by the Mathematical Association of America.)
- Alonso Del Arte (February 2019). "A future president once published a mathematical proof". medium.com. Retrieved 29 November 2023.
- William Dunham (1994). The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems, and Personalities. New York: John Wiley & Sons. p. 99. ISBN 0-471-53656-3.
- Elisha Scan Loomis (1940). The Pythagorean Proposition (2 ed.). Washington DC: National Council of Teachers of Mathematics. p. 109. ISBN 978-0-87353-036-1. Retrieved 28 November 2023. (A collection of 370 different proofs of the Pythagorean theorem.)
 is a right-angled triangle with right angle at
is a right-angled triangle with right angle at  . The side-lengths of the triangle are
. The side-lengths of the triangle are  . Pythagorean theorem asserts that
. Pythagorean theorem asserts that  .
.
 perpendicular to
perpendicular to  and on this line chose a point
and on this line chose a point  such that
such that  . Then, from
. Then, from  upon the extended line
upon the extended line  . From the figure, one can easily see that the triangles
. From the figure, one can easily see that the triangles  are congruent. Since
are congruent. Since  and
and  , they are parallel and so the quadrilateral
, they are parallel and so the quadrilateral  is a trapezoid. The theorem is proved by computing the area of this trapezoid in two different ways.
is a trapezoid. The theorem is proved by computing the area of this trapezoid in two different ways.
 .
.

