
In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.
For example, the totatives of n = 9 are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since gcd(9, 3) = gcd(9, 6) = 3 and gcd(9, 9) = 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since for n = 1 the only integer in the range from 1 to n is 1 itself, and gcd(1, 1) = 1.
Euler's totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime, then φ(mn) = φ(m)φ(n). This function gives the order of the multiplicative group of integers modulo n (the group of units of the ring ). It is also used for defining the RSA encryption system.
History, terminology, and notation
Leonhard Euler introduced the function in 1763. However, he did not at that time choose any specific symbol to denote it. In a 1784 publication, Euler studied the function further, choosing the Greek letter π to denote it: he wrote πD for "the multitude of numbers less than D, and which have no common divisor with it". This definition varies from the current definition for the totient function at D = 1 but is otherwise the same. The now-standard notation φ(A) comes from Gauss's 1801 treatise Disquisitiones Arithmeticae, although Gauss did not use parentheses around the argument and wrote φA. Thus, it is often called Euler's phi function or simply the phi function.
In 1879, J. J. Sylvester coined the term totient for this function, so it is also referred to as Euler's totient function, the Euler totient, or Euler's totient. Jordan's totient is a generalization of Euler's.
The cototient of n is defined as n − φ(n). It counts the number of positive integers less than or equal to n that have at least one prime factor in common with n.
Computing Euler's totient function
There are several formulae for computing φ(n).
Euler's product formula
It states
where the product is over the distinct prime numbers dividing n. (For notation, see Arithmetical function.)
An equivalent formulation is where is the prime factorization of (that is, are distinct prime numbers).
The proof of these formulae depends on two important facts.
Phi is a multiplicative function
This means that if gcd(m, n) = 1, then φ(m) φ(n) = φ(mn). Proof outline: Let A, B, C be the sets of positive integers which are coprime to and less than m, n, mn, respectively, so that |A| = φ(m), etc. Then there is a bijection between A × B and C by the Chinese remainder theorem.
Value of phi for a prime power argument
If p is prime and k ≥ 1, then
Proof: Since p is a prime number, the only possible values of gcd(p, m) are 1, p, p, ..., p, and the only way to have gcd(p, m) > 1 is if m is a multiple of p, that is, m ∈ {p, 2p, 3p, ..., pp = p}, and there are p such multiples not greater than p. Therefore, the other p − p numbers are all relatively prime to p.
Proof of Euler's product formula
The fundamental theorem of arithmetic states that if n > 1 there is a unique expression where p1 < p2 < ... < pr are prime numbers and each ki ≥ 1. (The case n = 1 corresponds to the empty product.) Repeatedly using the multiplicative property of φ and the formula for φ(p) gives
This gives both versions of Euler's product formula.
An alternative proof that does not require the multiplicative property instead uses the inclusion-exclusion principle applied to the set , excluding the sets of integers divisible by the prime divisors.
Example
In words: the distinct prime factors of 20 are 2 and 5; half of the twenty integers from 1 to 20 are divisible by 2, leaving ten; a fifth of those are divisible by 5, leaving eight numbers coprime to 20; these are: 1, 3, 7, 9, 11, 13, 17, 19.
The alternative formula uses only integers:
Fourier transform
The totient is the discrete Fourier transform of the gcd, evaluated at 1. Let
where xk = gcd(k,n) for k ∈ {1, ..., n}. Then
The real part of this formula is
For example, using and :Unlike the Euler product and the divisor sum formula, this one does not require knowing the factors of n. However, it does involve the calculation of the greatest common divisor of n and every positive integer less than n, which suffices to provide the factorization anyway.
Divisor sum
The property established by Gauss, that
where the sum is over all positive divisors d of n, can be proven in several ways. (See Arithmetical function for notational conventions.)
One proof is to note that φ(d) is also equal to the number of possible generators of the cyclic group Cd ; specifically, if Cd = ⟨g⟩ with g = 1, then g is a generator for every k coprime to d. Since every element of Cn generates a cyclic subgroup, and each subgroup Cd ⊆ Cn is generated by precisely φ(d) elements of Cn, the formula follows. Equivalently, the formula can be derived by the same argument applied to the multiplicative group of the nth roots of unity and the primitive dth roots of unity.
The formula can also be derived from elementary arithmetic. For example, let n = 20 and consider the positive fractions up to 1 with denominator 20:
Put them into lowest terms:
These twenty fractions are all the positive k/d ≤ 1 whose denominators are the divisors d = 1, 2, 4, 5, 10, 20. The fractions with 20 as denominator are those with numerators relatively prime to 20, namely 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20; by definition this is φ(20) fractions. Similarly, there are φ(10) fractions with denominator 10, and φ(5) fractions with denominator 5, etc. Thus the set of twenty fractions is split into subsets of size φ(d) for each d dividing 20. A similar argument applies for any n.
Möbius inversion applied to the divisor sum formula gives
where μ is the Möbius function, the multiplicative function defined by and for each prime p and k ≥ 2. This formula may also be derived from the product formula by multiplying out to get
An example:
Some values
The first 100 values (sequence A000010 in the OEIS) are shown in the table and graph below:
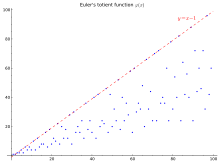
φ(n) for 1 ≤ n ≤ 100 + 1 2 3 4 5 6 7 8 9 10 0 1 1 2 2 4 2 6 4 6 4 10 10 4 12 6 8 8 16 6 18 8 20 12 10 22 8 20 12 18 12 28 8 30 30 16 20 16 24 12 36 18 24 16 40 40 12 42 20 24 22 46 16 42 20 50 32 24 52 18 40 24 36 28 58 16 60 60 30 36 32 48 20 66 32 44 24 70 70 24 72 36 40 36 60 24 78 32 80 54 40 82 24 64 42 56 40 88 24 90 72 44 60 46 72 32 96 42 60 40
In the graph at right the top line y = n − 1 is an upper bound valid for all n other than one, and attained if and only if n is a prime number. A simple lower bound is , which is rather loose: in fact, the lower limit of the graph is proportional to n/log log n.
Euler's theorem
Main article: Euler's theoremThis states that if a and n are relatively prime then
The special case where n is prime is known as Fermat's little theorem.
This follows from Lagrange's theorem and the fact that φ(n) is the order of the multiplicative group of integers modulo n.
The RSA cryptosystem is based on this theorem: it implies that the inverse of the function a ↦ a mod n, where e is the (public) encryption exponent, is the function b ↦ b mod n, where d, the (private) decryption exponent, is the multiplicative inverse of e modulo φ(n). The difficulty of computing φ(n) without knowing the factorization of n is thus the difficulty of computing d: this is known as the RSA problem which can be solved by factoring n. The owner of the private key knows the factorization, since an RSA private key is constructed by choosing n as the product of two (randomly chosen) large primes p and q. Only n is publicly disclosed, and given the difficulty to factor large numbers we have the guarantee that no one else knows the factorization.
Other formulae
-
In particular:
-
Compare this to the formula (see least common multiple).
- φ(n) is even for n ≥ 3.
Moreover, if n has r distinct odd prime factors, 2 | φ(n)
- For any a > 1 and n > 6 such that 4 ∤ n there exists an l ≥ 2n such that l | φ(a − 1).
-
where rad(n) is the radical of n (the product of all distinct primes dividing n).
- ( cited in)
-
(where γ is the Euler–Mascheroni constant).
Menon's identity
Main article: Menon's identityIn 1965 P. Kesava Menon proved
where d(n) = σ0(n) is the number of divisors of n.
Divisibility by any fixed positive integer
The following property, which is part of the « folklore » (i.e., apparently unpublished as a specific result: see the introduction of this article in which it is stated as having « long been known ») has important consequences. For instance it rules out uniform distribution of the values of in the arithmetic progressions modulo for any integer .
- For every fixed positive integer , the relation holds for almost all , meaning for all but values of as .
This is an elementary consequence of the fact that the sum of the reciprocals of the primes congruent to 1 modulo diverges, which itself is a corollary of the proof of Dirichlet's theorem on arithmetic progressions.
Generating functions
The Dirichlet series for φ(n) may be written in terms of the Riemann zeta function as:
where the left-hand side converges for .
The Lambert series generating function is
which converges for |q| < 1.
Both of these are proved by elementary series manipulations and the formulae for φ(n).
Growth rate
In the words of Hardy & Wright, the order of φ(n) is "always 'nearly n'."
First
but as n goes to infinity, for all δ > 0
These two formulae can be proved by using little more than the formulae for φ(n) and the divisor sum function σ(n).
In fact, during the proof of the second formula, the inequality
true for n > 1, is proved.
We also have
Here γ is Euler's constant, γ = 0.577215665..., so e = 1.7810724... and e = 0.56145948....
Proving this does not quite require the prime number theorem. Since log log n goes to infinity, this formula shows that
In fact, more is true.
and
The second inequality was shown by Jean-Louis Nicolas. Ribenboim says "The method of proof is interesting, in that the inequality is shown first under the assumption that the Riemann hypothesis is true, secondly under the contrary assumption."
For the average order, we have
due to Arnold Walfisz, its proof exploiting estimates on exponential sums due to I. M. Vinogradov and N. M. Korobov. By a combination of van der Corput's and Vinogradov's methods, H.-Q. Liu (On Euler's function.Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), no. 4, 769–775) improved the error term to
(this is currently the best known estimate of this type). The "Big O" stands for a quantity that is bounded by a constant times the function of n inside the parentheses (which is small compared to n).
This result can be used to prove that the probability of two randomly chosen numbers being relatively prime is 6/π.
Ratio of consecutive values
In 1950 Somayajulu proved
In 1954 Schinzel and Sierpiński strengthened this, proving that the set
is dense in the positive real numbers. They also proved that the set
is dense in the interval (0,1).
Totient numbers
A totient number is a value of Euler's totient function: that is, an m for which there is at least one n for which φ(n) = m. The valency or multiplicity of a totient number m is the number of solutions to this equation. A nontotient is a natural number which is not a totient number. Every odd integer exceeding 1 is trivially a nontotient. There are also infinitely many even nontotients, and indeed every positive integer has a multiple which is an even nontotient.
The number of totient numbers up to a given limit x is
for a constant C = 0.8178146....
If counted accordingly to multiplicity, the number of totient numbers up to a given limit x is
where the error term R is of order at most x/(log x) for any positive k.
It is known that the multiplicity of m exceeds m infinitely often for any δ < 0.55655.
Ford's theorem
Ford (1999) proved that for every integer k ≥ 2 there is a totient number m of multiplicity k: that is, for which the equation φ(n) = m has exactly k solutions; this result had previously been conjectured by Wacław Sierpiński, and it had been obtained as a consequence of Schinzel's hypothesis H. Indeed, each multiplicity that occurs, does so infinitely often.
However, no number m is known with multiplicity k = 1. Carmichael's totient function conjecture is the statement that there is no such m.
Perfect totient numbers
Main article: Perfect totient numberA perfect totient number is an integer that is equal to the sum of its iterated totients. That is, we apply the totient function to a number n, apply it again to the resulting totient, and so on, until the number 1 is reached, and add together the resulting sequence of numbers; if the sum equals n, then n is a perfect totient number.
Applications
Cyclotomy
Main article: Constructible polygonIn the last section of the Disquisitiones Gauss proves that a regular n-gon can be constructed with straightedge and compass if φ(n) is a power of 2. If n is a power of an odd prime number the formula for the totient says its totient can be a power of two only if n is a first power and n − 1 is a power of 2. The primes that are one more than a power of 2 are called Fermat primes, and only five are known: 3, 5, 17, 257, and 65537. Fermat and Gauss knew of these. Nobody has been able to prove whether there are any more.
Thus, a regular n-gon has a straightedge-and-compass construction if n is a product of distinct Fermat primes and any power of 2. The first few such n are
Prime number theorem for arithmetic progressions
Main article: Prime number theorem § Prime number theorem for arithmetic progressionsThe RSA cryptosystem
Main article: RSA (algorithm)Setting up an RSA system involves choosing large prime numbers p and q, computing n = pq and k = φ(n), and finding two numbers e and d such that ed ≡ 1 (mod k). The numbers n and e (the "encryption key") are released to the public, and d (the "decryption key") is kept private.
A message, represented by an integer m, where 0 < m < n, is encrypted by computing S = m (mod n).
It is decrypted by computing t = S (mod n). Euler's Theorem can be used to show that if 0 < t < n, then t = m.
The security of an RSA system would be compromised if the number n could be efficiently factored or if φ(n) could be efficiently computed without factoring n.
Unsolved problems
Lehmer's conjecture
Main article: Lehmer's totient problemIf p is prime, then φ(p) = p − 1. In 1932 D. H. Lehmer asked if there are any composite numbers n such that φ(n) divides n − 1. None are known.
In 1933 he proved that if any such n exists, it must be odd, square-free, and divisible by at least seven primes (i.e. ω(n) ≥ 7). In 1980 Cohen and Hagis proved that n > 10 and that ω(n) ≥ 14. Further, Hagis showed that if 3 divides n then n > 10 and ω(n) ≥ 298848.
Carmichael's conjecture
Main article: Carmichael's totient function conjectureThis states that there is no number n with the property that for all other numbers m, m ≠ n, φ(m) ≠ φ(n). See Ford's theorem above.
As stated in the main article, if there is a single counterexample to this conjecture, there must be infinitely many counterexamples, and the smallest one has at least ten billion digits in base 10.
Riemann hypothesis
The Riemann hypothesis is true if and only if the inequality
is true for all n ≥ p120569# where γ is Euler's constant and p120569# is the product of the first 120569 primes.
See also
Notes
- "Euler's totient function". Khan Academy. Retrieved 2016-02-26.
- Long (1972, p. 85)
- Pettofrezzo & Byrkit (1970, p. 72)
- Long (1972, p. 162)
- Pettofrezzo & Byrkit (1970, p. 80)
- See Euler's theorem.
- L. Euler "Theoremata arithmetica nova methodo demonstrata" (An arithmetic theorem proved by a new method), Novi commentarii academiae scientiarum imperialis Petropolitanae (New Memoirs of the Saint-Petersburg Imperial Academy of Sciences), 8 (1763), 74–104. (The work was presented at the Saint-Petersburg Academy on October 15, 1759. A work with the same title was presented at the Berlin Academy on June 8, 1758). Available on-line in: Ferdinand Rudio, ed., Leonhardi Euleri Commentationes Arithmeticae, volume 1, in: Leonhardi Euleri Opera Omnia, series 1, volume 2 (Leipzig, Germany, B. G. Teubner, 1915), pages 531–555. On page 531, Euler defines n as the number of integers that are smaller than N and relatively prime to N (... aequalis sit multitudini numerorum ipso N minorum, qui simul ad eum sint primi, ...), which is the phi function, φ(N).
- ^ Sandifer, p. 203
- Graham et al. p. 133 note 111
- L. Euler, Speculationes circa quasdam insignes proprietates numerorum, Acta Academiae Scientarum Imperialis Petropolitinae, vol. 4, (1784), pp. 18–30, or Opera Omnia, Series 1, volume 4, pp. 105–115. (The work was presented at the Saint-Petersburg Academy on October 9, 1775).
- Both φ(n) and ϕ(n) are seen in the literature. These are two forms of the lower-case Greek letter phi.
- Gauss, Disquisitiones Arithmeticae article 38
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing Company. §409.
- J. J. Sylvester (1879) "On certain ternary cubic-form equations", American Journal of Mathematics, 2 : 357-393; Sylvester coins the term "totient" on page 361.
- "totient". Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
- Schramm (2008)
- Gauss, DA, art 39
- Gauss, DA art. 39, arts. 52-54
- Graham et al. pp. 134-135
- ^ Hardy & Wright 1979, thm. 328
- Dineva (in external refs), prop. 1
- ^ Walfisz, Arnold (1963). Weylsche Exponentialsummen in der neueren Zahlentheorie. Mathematische Forschungsberichte (in German). Vol. 16. Berlin: VEB Deutscher Verlag der Wissenschaften. Zbl 0146.06003.
- Lomadse, G. (1964), "The scientific work of Arnold Walfisz" (PDF), Acta Arithmetica, 10 (3): 227–237, doi:10.4064/aa-10-3-227-237
- ^ Sitaramachandrarao, R. (1985). "On an error term of Landau II". Rocky Mountain J. Math. 15 (2): 579–588. doi:10.1216/RMJ-1985-15-2-579.
- Pollack, P. (2023), "Two problems on the distribution of Carmichael's lambda function", Mathematika, 69 (4): 1195–1220, arXiv:2303.14043, doi:10.1112/mtk.12222
- Hardy & Wright 1979, thm. 288
- Hardy & Wright 1979, thm. 309
- Hardy & Wright 1979, intro to § 18.4
- Hardy & Wright 1979, thm. 326
- Hardy & Wright 1979, thm. 327
- In fact Chebyshev's theorem (Hardy & Wright 1979, thm.7) and Mertens' third theorem is all that is needed.
- Hardy & Wright 1979, thm. 436
- Theorem 15 of Rosser, J. Barkley; Schoenfeld, Lowell (1962). "Approximate formulas for some functions of prime numbers". Illinois J. Math. 6 (1): 64–94. doi:10.1215/ijm/1255631807.
- Bach & Shallit, thm. 8.8.7
- ^ Ribenboim (1989). "How are the Prime Numbers Distributed? §I.C The Distribution of Values of Euler's Function". The Book of Prime Number Records (2nd ed.). New York: Springer-Verlag. pp. 172–175. doi:10.1007/978-1-4684-0507-1_5. ISBN 978-1-4684-0509-5.
- Sándor, Mitrinović & Crstici (2006) pp.24–25
- Hardy & Wright 1979, thm. 332
- ^ Ribenboim, p.38
- ^ Sándor, Mitrinović & Crstici (2006) p.16
- ^ Guy (2004) p.144
- Sándor & Crstici (2004) p.230
- Zhang, Mingzhi (1993). "On nontotients". Journal of Number Theory. 43 (2): 168–172. doi:10.1006/jnth.1993.1014. ISSN 0022-314X. Zbl 0772.11001.
- ^ Ford, Kevin (1998). "The distribution of totients". Ramanujan J. 2 (1–2): 67–151. doi:10.1023/A:1009761909132. ISSN 1382-4090. Zbl 0914.11053. Reprinted in Analytic and Elementary Number Theory: A Tribute to Mathematical Legend Paul Erdos, Developments in Mathematics, vol. 1, 1998, doi:10.1007/978-1-4757-4507-8_8, ISBN 978-1-4419-5058-1. Updated and corrected in arXiv:1104.3264, 2011.
- Sándor et al (2006) p.22
- Sándor et al (2006) p.21
- ^ Guy (2004) p.145
- Sándor & Crstici (2004) p.229
- Sándor & Crstici (2004) p.228
- Gauss, DA. The 7th § is arts. 336–366
- Gauss proved if n satisfies certain conditions then the n-gon can be constructed. In 1837 Pierre Wantzel proved the converse, if the n-gon is constructible, then n must satisfy Gauss's conditions
- Gauss, DA, art 366
- Gauss, DA, art. 366. This list is the last sentence in the Disquisitiones
- Ribenboim, pp. 36–37.
- Cohen, Graeme L.; Hagis, Peter Jr. (1980). "On the number of prime factors of n if φ(n) divides n − 1". Nieuw Arch. Wiskd. III Series. 28: 177–185. ISSN 0028-9825. Zbl 0436.10002.
- Hagis, Peter Jr. (1988). "On the equation M·φ(n) = n − 1". Nieuw Arch. Wiskd. IV Series. 6 (3): 255–261. ISSN 0028-9825. Zbl 0668.10006.
- Guy (2004) p.142
- Broughan, Kevin (2017). Equivalents of the Riemann Hypothesis, Volume One: Arithmetic Equivalents (First ed.). Cambridge University Press. ISBN 978-1-107-19704-6. Corollary 5.35
References
The Disquisitiones Arithmeticae has been translated from Latin into English and German. The German edition includes all of Gauss's papers on number theory: all the proofs of quadratic reciprocity, the determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes.
References to the Disquisitiones are of the form Gauss, DA, art. nnn.
- Abramowitz, M.; Stegun, I. A. (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN 0-486-61272-4. See paragraph 24.3.2.
- Bach, Eric; Shallit, Jeffrey (1996), Algorithmic Number Theory (Vol I: Efficient Algorithms), MIT Press Series in the Foundations of Computing, Cambridge, MA: The MIT Press, ISBN 0-262-02405-5, Zbl 0873.11070
- Dickson, Leonard Eugene, "History Of The Theory Of Numbers", vol 1, chapter 5 "Euler's Function, Generalizations; Farey Series", Chelsea Publishing 1952
- Ford, Kevin (1999), "The number of solutions of φ(x) = m", Annals of Mathematics, 150 (1): 283–311, doi:10.2307/121103, ISSN 0003-486X, JSTOR 121103, MR 1715326, Zbl 0978.11053.
- Gauss, Carl Friedrich (1986), Disquisitiones Arithmeticae (Second, corrected edition), translated by Clarke, Arthur A., New York: Springer, ISBN 0-387-96254-9
- Gauss, Carl Friedrich (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition), translated by Maser, H., New York: Chelsea, ISBN 0-8284-0191-8
- Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994), Concrete Mathematics: a foundation for computer science (2nd ed.), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5, Zbl 0836.00001
- Guy, Richard K. (2004), Unsolved Problems in Number Theory, Problem Books in Mathematics (3rd ed.), New York, NY: Springer-Verlag, ISBN 0-387-20860-7, Zbl 1058.11001
- Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (Fifth ed.), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Liu, H.-Q. (2016), "On Euler's function", Proc. Roy. Soc. Edinburgh Sect. A, 146 (4): 769–775, doi:10.1017/S0308210515000682.
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77-171950
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766
- Ribenboim, Paulo (1996), The New Book of Prime Number Records (3rd ed.), New York: Springer, ISBN 0-387-94457-5, Zbl 0856.11001
- Sandifer, Charles (2007), The early mathematics of Leonhard Euler, MAA, ISBN 978-0-88385-559-1
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006), Handbook of number theory I, Dordrecht: Springer-Verlag, pp. 9–36, ISBN 1-4020-4215-9, Zbl 1151.11300
- Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 179–327. ISBN 1-4020-2546-7. Zbl 1079.11001.
- Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor", Electronic Journal of Combinatorial Number Theory, A50 (8(1)).
External links
- "Totient function", Encyclopedia of Mathematics, EMS Press, 2001
- Euler's Phi Function and the Chinese Remainder Theorem — proof that φ(n) is multiplicative Archived 2021-02-28 at the Wayback Machine
- Euler's totient function calculator in JavaScript — up to 20 digits
- Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions Archived 2021-01-16 at the Wayback Machine
- Plytage, Loomis, Polhill Summing Up The Euler Phi Function
| Totient function | |
|---|---|
|
 or
or  , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the
, and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the  ). It is also used for defining the
). It is also used for defining the 
 where
where  is the
is the  (that is,
(that is,  are distinct prime numbers).
are distinct prime numbers).

 where p1 < p2 < ... < pr are
where p1 < p2 < ... < pr are 
 , excluding the sets of integers divisible by the prime divisors.
, excluding the sets of integers divisible by the prime divisors.





 and
and  :
: Unlike the Euler product and the divisor sum formula, this one does not require knowing the factors of n. However, it does involve the calculation of the greatest common divisor of n and every positive integer less than n, which suffices to provide the factorization anyway.
Unlike the Euler product and the divisor sum formula, this one does not require knowing the factors of n. However, it does involve the calculation of the greatest common divisor of n and every positive integer less than n, which suffices to provide the factorization anyway.




 and
and  for each prime p and k ≥ 2. This formula may also be derived from the product formula by multiplying out
for each prime p and k ≥ 2. This formula may also be derived from the product formula by multiplying out  to get
to get 

 , which is rather loose: in fact, the
, which is rather loose: in fact, the 






 (see
(see 


 ( cited in)
( cited in)




 for any integer
for any integer  .
.
 holds for almost all
holds for almost all  values of
values of  as
as  .
.
 .
.















