| Part of a series on |
| Antennas |
|---|
 |
| Common types |
| Components |
| Systems |
| Safety and regulation |
| Radiation sources / regions |
| Characteristics |
| Techniques |
In electrical engineering, electrical length is a dimensionless parameter equal to the physical length of an electrical conductor such as a cable or wire, divided by the wavelength of alternating current at a given frequency traveling through the conductor. In other words, it is the length of the conductor measured in wavelengths. It can alternately be expressed as an angle, in radians or degrees, equal to the phase shift the alternating current experiences traveling through the conductor.
Electrical length is defined for a conductor operating at a specific frequency or narrow band of frequencies. It is determined by the construction of the cable, so different cables of the same length operating at the same frequency can have different electrical lengths. A conductor is called electrically long if it has an electrical length much greater than one; that is it is much longer than the wavelength of the alternating current passing through it, and electrically short if it is much shorter than a wavelength. Electrical lengthening and electrical shortening means adding reactance (capacitance or inductance) to an antenna or conductor to increase or decrease the electrical length, usually for the purpose of making it resonant at a different resonant frequency.
This concept is used throughout electronics, and particularly in radio frequency circuit design, transmission line and antenna theory and design. Electrical length determines when wave effects (phase shift along conductors) become important in a circuit. Ordinary lumped element electric circuits only work well for alternating currents at frequencies for which the circuit is electrically small (electrical length much less than one). For frequencies high enough that the wavelength approaches the size of the circuit (the electrical length approaches one) the lumped element model on which circuit theory is based becomes inaccurate, and transmission line techniques must be used.
Definition

Electrical length is defined for conductors carrying alternating current (AC) at a single frequency or narrow band of frequencies. An alternating electric current of a single frequency is an oscillating sine wave which repeats with a period of . This current flows through a given conductor such as a wire or cable at a particular phase velocity . It takes time for later portions of the wave to reach a given point on the conductor so the spatial distribution of current and voltage along the conductor at any time is a moving sine wave. After a time equal to the period a complete cycle of the wave has passed a given point and the wave repeats; during this time a point of constant phase on the wave has traveled a distance of
so (Greek lambda) is the wavelength of the wave along the conductor, the distance between successive crests of the wave.
The electrical length of a conductor with a physical length of at a given frequency is the number of wavelengths or fractions of a wavelength of the wave along the conductor; in other words the conductor's length measured in wavelengths
The phase velocity at which electrical signals travel along a transmission line or other cable depends on the construction of the line. Therefore, the wavelength corresponding to a given frequency varies in different types of lines, thus at a given frequency different conductors of the same physical length can have different electrical lengths.
Phase shift definition
In radio frequency applications, when a delay is introduced due to a conductor, it is often the phase shift , the difference in phase of the sinusoidal wave between the two ends of the conductor, that is of importance. The length of a sinusoidal wave is commonly expressed as an angle, in units of degrees (with 360° in a wavelength) or radians (with 2π radians in a wavelength). So alternately the electrical length can be expressed as an angle which is the phase shift of the wave between the ends of the conductor
Significance
The electrical length of a conductor determines when wave effects (phase shift along the conductor) are important. If the electrical length is much less than one, that is the physical length of a conductor is much shorter than the wavelength, say less than one tenth of the wavelength () it is called electrically short. In this case the voltage and current are approximately constant along the conductor, so it acts as a simple connector which transfers alternating current with negligible phase shift. In circuit theory the connecting wires between components are usually assumed to be electrically short, so the lumped element circuit model is only valid for alternating current when the circuit is electrically small, much smaller than a wavelength. When the electrical length approaches or is greater than one, a conductor will have significant reactance, inductance or capacitance, depending on its length. So simple circuit theory is inadequate and transmission line techniques (the distributed-element model) must be used.
Velocity factor
In a vacuum an electromagnetic wave (radio wave) travels at the speed of light 2.9979×10 meters per second, and very close to this speed in air, so the free space wavelength of the wave is . (in this article free space variables are distinguished by a subscript 0) Thus a physical length of a radio wave in space or air has an electrical length of
- wavelengths.
In the SI system of units, empty space has a permittivity of 8.854×10 F/m (farads per metre) and a magnetic permeability of 1.257×10 H/m (henries per meter). These universal constants determine the speed of light

In an electrical cable, for a cycle of the alternating current to move a given distance along the line, it takes time to charge the capacitance between the conductors, and the rate of change of the current is slowed by the series inductance of the wires. This determines the phase velocity at which the wave moves along the line. In cables and transmission lines an electrical signal travels at a rate determined by the effective shunt capacitance and series inductance per unit length of the transmission line
Some transmission lines consist only of bare metal conductors, if they are far away from other high permittivity materials their signals propagate at very close to the speed of light, . In most transmission lines the material construction of the line slows the velocity of the signal so it travels at a reduced phase velocity
where (kappa) is a dimensionless number between 0 and 1 called the velocity factor (VF), characteristic of the type of line, equal to the ratio of signal velocity in the line to the speed of light.
Most transmission lines contain a dielectric material (insulator) filling some or all of the space in between the conductors. The permittivity or dielectric constant of that material increases the distributed capacitance in the cable, which reduces the velocity factor below unity. If there is a material with high magnetic permeability () in the line such as steel or ferrite which increases the distributed inductance , it can also reduce , but this is almost never the case. If all the space around the transmission line conductors containing the near fields was filled with a material of permittivity and permeability , the phase velocity on the line would be
The effective permittivity and permeability per unit length of the line are frequently given as dimensionless constants; relative permittivity: and relative permeability: equal to the ratio of these parameters compared to the universal constants and
so the phase velocity is
So the velocity factor of the line is
In many lines, for example twin lead, only a fraction of the space surrounding the line containing the fields is occupied by a solid dielectric. With only part of the electromagnetic field effected by the dielectric, there is less reduction of the wave velocity. In this case an effective permittivity can be calculated which if it filled all the space around the line would give the same phase velocity. This is computed as a weighted average of the relative permittivity of free space, unity, and that of the dielectric: where the fill factor F expresses the effective proportion of space around the line occupied by dielectric.
In most transmission lines there are no materials with high magnetic permeability, so and and so
(no magnetic materials)
Since the electromagnetic waves travel slower in the line than in free space, the wavelength of the wave in the transmission line is shorter than the free space wavelength by the factor kappa: . Therefore, more wavelengths fit in a transmission line of a given length than in the same length of wave in free space, so the electrical length of a transmission line is longer than the electrical length of a wave of the same frequency in free space
Transmission lines
| Type of line | Velocity factor κ |
Velocity of signal in cm per ns | |
|---|---|---|---|
| Parallel line, air dielectric |
.95 | 29 | |
| Parallel line, polyethylene dielectric (Twin lead) |
.85 | 28 | |
| Coaxial cable, polyethylene dielectric |
.66 | 20 | |
| Twisted pair, CAT-5 | .64 | 19 | |
| Stripline | .50 | 15 | |
| Microstrip | .50 | 15 |
Ordinary electrical cable suffices to carry alternating current when the cable is electrically short; the electrical length of the cable is small compared to one, that is when the physical length of the cable is small compared to a wavelength, say .
As frequency gets high enough that the length of the cable becomes a significant fraction of a wavelength, , ordinary wires and cables become poor conductors of AC. Impedance discontinuities at the source, load, connectors and switches begin to reflect the electromagnetic current waves back toward the source, creating bottlenecks so not all the power reaches the load. Ordinary wires act as antennas, radiating the power into space as radio waves, and in radio receivers can also pick up radio frequency interference (RFI).
To mitigate these problems, at these frequencies transmission line is used instead. A transmission line is a specialized cable designed for carrying electric current of radio frequency. The distinguishing feature of a transmission line is that it is constructed to have a constant characteristic impedance along its length and through connectors and switches, to prevent reflections. This also means AC current travels at a constant phase velocity along its length, while in ordinary cable phase velocity may vary. The velocity factor depends on the details of construction, and is different for each type of transmission line. However the approximate velocity factor for the major types of transmission lines is given in the table.
Electrical length is widely used with a graphical aid called the Smith chart to solve transmission line calculations. A Smith chart has a scale around the circumference of the circular chart graduated in wavelengths and degrees, which represents the electrical length of the transmission line from the point of measurement to the source or load.
The equation for the voltage as a function of time along a transmission line with a matched load, so there is no reflected power, is
where
- is the peak voltage along the line
- is the angular frequency of the alternating current in radians per second
- is the wavenumber, equal to the number of radians of the wave in one meter
- is the distance along the line
- is time
In a matched transmission line, the current is in phase with the voltage, and their ratio is the characteristic impedance of the line
Antennas
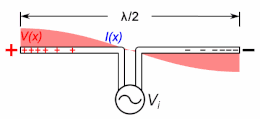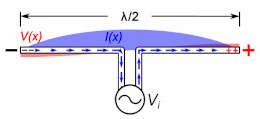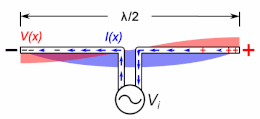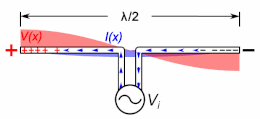
An important class of radio antenna is the thin element antenna in which the radiating elements are conductive wires or rods. These include monopole antennas and dipole antennas, as well as antennas based on them such as the whip antenna, T antenna, mast radiator, Yagi, log periodic, and turnstile antennas. These are resonant antennas, in which the radio frequency electric currents travel back and forth in the antenna conductors, reflecting from the ends.
If the antenna rods are not too thick (have a large enough length to diameter ratio), the current along them is close to a sine wave, so the concept of electrical length also applies to these. The current is in the form of two oppositely directed sinusoidal traveling waves which reflect from the ends, which interfere to form standing waves. The electrical length of an antenna, like a transmission line, is its length in wavelengths of the current on the antenna at the operating frequency. An antenna's resonant frequency, radiation pattern, and driving point impedance depend not on its physical length but on its electrical length. A thin antenna element is resonant at frequencies at which the standing current wave has a node (zero) at the ends (and in monopoles an antinode (maximum) at the ground plane). A dipole antenna is resonant at frequencies at which its electrical length is a half wavelength () or a multiple of it. A monopole antenna is resonant at frequencies at which its electrical length is a quarter wavelength () or a multiple of it.
Resonant frequency is important because at frequencies at which the antenna is resonant the input impedance it presents to its feedline is purely resistive. If the resistance of the antenna is matched to the characteristic resistance of the feedline, it absorbs all the power supplied to it, while at other frequencies it has reactance and reflects some power back down the line toward the transmitter, causing standing waves (high SWR) on the feedline. Since only a portion of the power is radiated this causes inefficiency, and can possibly overheat the line or transmitter. Therefore, transmitting antennas are usually designed to be resonant at the transmitting frequency; and if they cannot be made the right length they are electrically lengthened or shortened to be resonant (see below).
End effects

A thin-element antenna can be thought of as a transmission line with the conductors separated, so the near-field electric and magnetic fields extend further into space than in a transmission line, in which the fields are mainly confined to the vicinity of the conductors. Near the ends of the antenna elements the electric field is not perpendicular to the conductor axis as in a transmission line but spreads out in a fan shape (fringing field). As a result, the end sections of the antenna have increased capacitance, storing more charge, so the current waveform departs from a sine wave there, decreasing faster toward the ends. When approximated as a sine wave, the current does not quite go to zero at the ends; the nodes of the current standing wave, instead of being at the ends of the element, occur somewhat beyond the ends. Thus the electrical length of the antenna is longer than its physical length.
The electrical length of an antenna element also depends on the length-to-diameter ratio of the conductor. As the ratio of the diameter to wavelength increases, the capacitance increases, so the node occurs farther beyond the end, and the electrical length of the element increases. When the elements get too thick, the current waveform becomes significantly different from a sine wave, so the entire concept of electrical length is no longer applicable, and the behavior of the antenna must be calculated by electromagnetic simulation computer programs like NEC.
As with a transmission line, an antenna's electrical length is increased by anything that adds shunt capacitance or series inductance to it, such as the presence of high permittivity dielectric material around it. In microstrip antennas which are fabricated as metal strips on printed circuit boards, the dielectric constant of the substrate board increases the electrical length of the antenna. Proximity to the Earth or a ground plane, a dielectric coating on the conductor, nearby grounded towers, metal structural members, guy lines and the capacitance of insulators supporting the antenna also increase the electrical length.
These factors, called "end effects", cause the electrical length of an antenna element to be somewhat longer than the length of the same wave in free space. In other words, the physical length of the antenna at resonance will be somewhat shorter than the resonant length in free space (one-half wavelength for a dipole, one-quarter wavelength for a monopole). As a rough generalization, for a typical dipole antenna, the physical resonant length is about 5% shorter than the free space resonant length.
Electrical lengthening and shortening
In many circumstances for practical reasons it is inconvenient or impossible to use an antenna of resonant length. An antenna of nonresonant length at the operating frequency can be made resonant by adding a reactance, a capacitance or inductance, either in the antenna itself or in a matching network between the antenna and its feedline. A nonresonant antenna appears at its feedpoint electrically equivalent to a resistance in series with a reactance. Adding an equal but opposite type of reactance in series with the feedline will cancel the antenna's reactance; the combination of the antenna and reactance will act as a series resonant circuit, so at its operating frequency its input impedance will be purely resistive, allowing it to be fed power efficiently at a low SWR without reflections.
In a common application, an antenna which is electrically short, shorter than its fundamental resonant length, a monopole antenna with an electrical length shorter than a quarter-wavelength (), or a dipole antenna shorter than a half-wavelength () will have capacitive reactance. Adding an inductor (coil of wire), called a loading coil, at the feedpoint in series with the antenna, with inductive reactance equal to the antenna's capacitive reactance at the operating frequency, will cancel the capacitance of the antenna, so the combination of the antenna and coil will be resonant at the operating frequency. Since adding inductance is equivalent to increasing the electrical length, this technique is called electrically lengthening the antenna. This is the usual technique for matching an electrically short transmitting antenna to its feedline, so it can be fed power efficiently. However, an electrically short antenna that has been loaded in this way still has the same radiation pattern; it does not radiate as much power, and therefore has lower gain than a full-sized antenna.
Conversely, an antenna longer than resonant length at its operating frequency, such as a monopole longer than a quarter wavelength but shorter than a half wavelength, will have inductive reactance. This can be cancelled by adding a capacitor of equal but opposite reactance at the feed point to make the antenna resonant. This is called electrically shortening the antenna.
Scaling properties of antennas
Two antennas that are similar (scaled copies of each other), fed with different frequencies, will have the same radiation resistance and radiation pattern and fed with equal power will radiate the same power density in any direction if they have the same electrical length at the operating frequency; that is, if their lengths are in the same proportion as the wavelengths.
This means the length of antenna required for a given antenna gain scales with the wavelength (inversely with the frequency), or equivalently the aperture scales with the square of the wavelength.
Electrically short antennas
An electrically short conductor, much shorter than one wavelength, makes an inefficient radiator of electromagnetic waves. As the length of an antenna is made shorter than its fundamental resonant length (a half-wavelength for a dipole antenna and a quarter-wavelength for a monopole), the radiation resistance the antenna presents to the feedline decreases with the square of the electrical length, that is the ratio of physical length to wavelength, . As a result, other resistances in the antenna, the ohmic resistance of metal antenna elements, the ground system if present, and the loading coil, dissipate an increasing fraction of transmitter power as heat. A monopole antenna with an electrical length below .05 or 18° has a radiation resistance of less than one ohm, making it very hard to drive.
A second disadvantage is that since the capacitive reactance of the antenna and inductive reactance of the required loading coil do not decrease, the Q factor of the antenna increases; it acts electrically like a high Q tuned circuit. As a result, the bandwidth of the antenna decreases with the square of electrical length, reducing the data rate that can be transmitted. At VLF frequencies even the huge toploaded wire antennas that must be used have bandwidths of only ~10 hertz, limiting the data rate that can be transmitted.
Regimes of electromagnetics
The field of electromagnetics is the study of electric fields, magnetic fields, electric charge, electric currents and electromagnetic waves. Classic electromagnetism is based on the solution of Maxwell's equations. These equations are mathematically difficult to solve in all generality, so approximate methods have been developed that apply to situations in which the electrical length of the apparatus is very short () or very long (). Electromagnetics is divided into three regimes or fields of study depending on the electrical length of the apparatus, that is the physical length of the apparatus compared to the wavelength of the waves: Completely different apparatus is used to conduct and process electromagnetic waves in these different wavelength ranges
- Circuit theory: When the wavelength of the electrical oscillations is much larger than the physical size of the circuit (), say , the action occurs in the near field. The phase of the oscillations and therefore the current and voltage can be approximated as constant along the length of connecting wires. Also little energy is radiated in the form of electromagnetic waves, the power radiated by a conductor as an antenna is proportional to the electrical length squared . So the electrical energy remains in the wires and components as quasistatic near-field electric and magnetic fields. Therefore, the approximation of the lumped element model can be used, and electric currents oscillating at these frequencies can be processed by electric circuits consisting of lumped circuit elements such as resistors, capacitors, inductors, transformers, transistors, and integrated circuits linked by ordinary wires. Mathematically Maxwell's equations reduce to circuit theory (Kirchhoff's circuit laws).
- , Distributed-element model (microwave theory): When the wavelength of the waves is of the same order of magnitude as the size of the equipment (), as it is in the microwave part of the spectrum, full solutions of Maxwell's equations must be used. At these frequencies, wires are replaced by transmission lines and waveguide and lumped elements are replaced by resonant stubs, irises, and cavity resonators. Often only a single mode (wave pattern) is propagating through the apparatus, which simplifies the mathematics. A modification of circuit theory called the distributed-element model can often be used, in which extended objects are regarded as electrical circuits with capacitance, inductance and resistance distributed along their length. A graphical aid called the Smith chart is often used to analyze transmission lines.
- , Optics: When the wavelength of the electromagnetic wave is much smaller than the physical size of the equipment that manipulates it (), say , most of the path of the waves is in the far field. In the far field, the electric and magnetic fields cannot be separated but propagate together as an electromagnetic wave. Unlike in the case of microwaves, unless coherent light sources like lasers are used, the number of modes propagating is usually large. Since little of the energy is stored in the quasistatic (induction) electric or magnetic fields at the surface boundaries between media (called evanescent fields in optics), the concepts of voltage, current, capacitance, and inductance have little meaning and are not used, and the medium is characterized by its index of refraction , absorption, permittivity , permeability , and dispersion. At these frequencies electromagnetic waves are manipulated by optical elements such as lenses, mirrors, prisms, optical filters and diffraction gratings. Maxwell's equations can be approximated by the equations of geometrical optics or physical optics.
Historically, electric circuit theory and optics developed as separate branches of physics until at the end of the 19th century James Clerk Maxwell's electromagnetic theory and Heinrich Hertz's discovery that light was electromagnetic waves unified these fields as branches of electromagnetism.
Definition of variables
| Symbol | Unit | Definition |
|---|---|---|
| meter | Wavenumber of wave in conductor | |
| farads / meter | Permittivity per meter of the dielectric in cable | |
| farads / meter | Permittivity of free space, a fundamental constant | |
| farads / meter | Effective relative permittivity per meter of cable | |
| none | Relative permittivity of the dielectric in cable | |
| none | Velocity factor of current in conductor | |
| meter | Wavelength of radio waves in conductor | |
| meter | Wavelength of radio waves in free space | |
| henries / meter | Effective magnetic permeability per meter of cable | |
| henries / meter | Permeability of free space, a fundamental constant | |
| none | Relative permeability of dielectric in cable | |
| none | Index of refraction of dielectric material | |
| none | Constant = 3.14159 | |
| radians or degrees | Phase shift of current between the ends of the conductor | |
| radians / second | Angular frequency of alternating current | |
| meters / second | Speed of light in vacuum | |
| farads / meter | Shunt capacitance per unit length of the conductor | |
| hertz | Frequency of radio waves | |
| none | Fill factor of a transmission line, the fraction of space filled with dielectric | |
| none | Electrical length of conductor | |
| none | Electrical length of electromagnetic wave of length l in free space | |
| meter | Length of the conductor | |
| henries / meter | Inductance per unit length of the conductor | |
| second | Period of radio waves | |
| second | time | |
| meters / second | phase velocity of current in conductor | |
| meter | distance along conductor |
References
- ^ "Electrical length". ATIS Telecom Glossary. Alliance for Telecommunications Industry Solutions website. 2019. Retrieved 24 December 2022. ANSI (American National Standards Institute) accredited definition
- ^ Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. CRC Press. pp. 3.1 – 3.2. ISBN 9780849320873.
- ^ Weik, Martin (2012). Communications Standard Dictionary. Springer. p. 283. ISBN 9781461304296.
- ^ Schmitt, Ron (2002). Electromagnetics Explained: A Handbook for Wireless RF, EMC, and High-Speed Electronics. Newnes. ISBN 9780750674034.
- ^ Paul, Clayton R. (2011). Transmission Lines in Digital and Analog Electronic Systems. Wiley. pp. 6–11. ISBN 9781118058244.
- ^ Drollinger, Francis J. (1980). Ground Radio Communications Specialist: Vol. 7 - Auxiliary circuits and systems. US Air Force Technical Training School. pp. 16–18.
- Rao, R. S. (2012). Electromagnetic Waves and Transmission Lines. PHI Learning. p. 445. ISBN 9788120345157.
- Carr, Joseph J. (1997). Microwave & Wireless Communications Technology. Newnes. p. 51. ISBN 0750697075.
- Amlaner, Charles J. Jr. (March 1979). "The design of antennas for use in radio telemetry". A Handbook on Biotelemetry and Radio Tracking: Proceedings of an International Conference on Telemetry and Radio Tracking in Biology and Medicine, Oxford, 20–22 March 1979. Elsevier. p. 260. Retrieved 23 November 2013.
- Keller, Reto B. (2022). Design for Electromagnetic Compatibility-In a Nutshell. Springer International. p. 39. ISBN 9783031141867.
- Keller, Reto (2018). "Chapter 5: Transmission lines". Electromagnetic compatibility knowledge base. Academy of EMC website. Retrieved 24 December 2022.
- ^ Radioman 3 & 2, US Navy Training Course NAVPERS 10228-E. Bureau of Naval Personnel, US Navy. 1967. p. 131.
- Singh, Yaduvir (2011). Electro Magnetic Field Theory. Dorling Kindersley. p. 451. ISBN 9788131760611.
- Griffith, B. Whitfield (2000). Radio-electronic Transmission Fundamentals. Noble Publishing. pp. 335–337. ISBN 9781884932137.
- ^ US Air Force Manual 52-19: Antenna Systems. US Air Force. 1953. pp. 104–105.
- Schelkunoff, Sergei A.; Friis, Harold T. (1952). Antennas: Theory and Practice. John Wiley and Sons. p. 245.
- Rudge, Alan W.; Milne, K. (1982). The Handbook of Antenna Design, Vol. 2. IET. p. 564. ISBN 9780906048870.
- The effect of this on the antenna is equivalent to the current wave moving along the antenna at a phase velocity lower than the speed of light , as in a transmission line. Some sources explain it this way: Carr, Joseph; Hippisley, George (2012). Practical Antenna Handbook, 5th Ed (PDF). McGraw-Hill. p. 105. ISBN 9780071639590. and Rudge, Alan W.; Milne, K. (1982). The Handbook of Antenna Design, Vol. 2. IET. p. 564. ISBN 9780906048870. However, this is a physically misleading description; the phase velocity is not constant along the element.
- ^ Lewis, Geoff (2013). Newnes Communications Technology Handbook. Elsevier. p. 46. ISBN 9781483101026.
- ^ The A.R.R.L. Antenna Book, 5th Ed. American Radio Relay League. 1949. pp. 27–28.
- Carr, Joseph (2001). Antenna Toolkit, 2nd Ed. Elsevier. pp. 52–54. ISBN 9780080493886.
- Levin, Boris (2019). Wide-Range Antennas. CRC Press. p. 26. ISBN 9781351043229.
- Azadeh, Mohammad (2009). Fiber Optics Engineering. Springer Science and Business Media. p. 11. ISBN 9781441903044.
- Pozar, David M. (2011). Microwave Engineering, 4th Ed. Wiley Global Education. pp. 1–2. ISBN 9781118213636.
- Karmel, Paul R.; Colef, Gabriel D.; Camisa, Raymond L. (1998). Introduction to Electromagnetic and Microwave Engineering. John Wiley and Sons. pp. 1–2. ISBN 9780471177814.
- Clark, Alan Robert; Fourie, Andre P. C. (2001). Antennas in Practice (PDF). Poynting Innovations. p. 3. ISBN 0620276193. Archived from the original (PDF) on 2023-01-02. Retrieved 2023-01-02.
 is an oscillating
is an oscillating  . This current flows through a given conductor such as a wire or cable at a particular
. This current flows through a given conductor such as a wire or cable at a particular  . It takes time for later portions of the wave to reach a given point on the conductor so the spatial distribution of current and voltage along the conductor at any time is a moving
. It takes time for later portions of the wave to reach a given point on the conductor so the spatial distribution of current and voltage along the conductor at any time is a moving  a complete cycle of the wave has passed a given point and the wave repeats; during this time a point of constant
a complete cycle of the wave has passed a given point and the wave repeats; during this time a point of constant 
 (Greek
(Greek  of a conductor with a physical length of
of a conductor with a physical length of  at a given frequency
at a given frequency 
 , the difference in
, the difference in 

 ) it is called electrically short. In this case the voltage and current are approximately constant along the conductor, so it acts as a simple connector which transfers alternating current with negligible phase shift. In
) it is called electrically short. In this case the voltage and current are approximately constant along the conductor, so it acts as a simple connector which transfers alternating current with negligible phase shift. In  2.9979×10 meters per second, and very close to this speed in air, so the free space wavelength of the wave is
2.9979×10 meters per second, and very close to this speed in air, so the free space wavelength of the wave is  . (in this article free space variables are distinguished by a subscript 0) Thus a physical length
. (in this article free space variables are distinguished by a subscript 0) Thus a physical length  wavelengths.
wavelengths. 8.854×10 F/m (farads per metre) and a
8.854×10 F/m (farads per metre) and a  1.257×10 H/m (henries per meter). These universal constants determine the speed of light
1.257×10 H/m (henries per meter). These universal constants determine the speed of light

 and
and  represent the
represent the 
 . In most transmission lines the material construction of the line slows the velocity of the signal so it travels at a reduced
. In most transmission lines the material construction of the line slows the velocity of the signal so it travels at a reduced 
 (kappa) is a dimensionless number between 0 and 1 called the
(kappa) is a dimensionless number between 0 and 1 called the  or dielectric constant of that material increases the distributed capacitance
or dielectric constant of that material increases the distributed capacitance  ) in the line such as steel or
) in the line such as steel or 
 and
and  equal to the ratio of these parameters compared to the universal constants
equal to the ratio of these parameters compared to the universal constants  and
and 



 can be calculated which if it filled all the space around the line would give the same phase velocity. This is computed as a weighted average of the relative permittivity of free space, unity, and that of the dielectric:
can be calculated which if it filled all the space around the line would give the same phase velocity. This is computed as a weighted average of the relative permittivity of free space, unity, and that of the dielectric:
 where the fill factor F expresses the effective proportion of space around the line occupied by dielectric.
where the fill factor F expresses the effective proportion of space around the line occupied by dielectric.
 and
and  and so
and so
 (no magnetic materials)
(no magnetic materials)
 . Therefore, more wavelengths fit in a transmission line of a given length
. Therefore, more wavelengths fit in a transmission line of a given length 
 , ordinary wires and cables become poor conductors of AC. Impedance discontinuities at the source, load, connectors and switches begin to reflect the electromagnetic current waves back toward the source, creating bottlenecks so not all the power reaches the load. Ordinary wires act as antennas, radiating the power into space as radio waves, and in radio receivers can also pick up
, ordinary wires and cables become poor conductors of AC. Impedance discontinuities at the source, load, connectors and switches begin to reflect the electromagnetic current waves back toward the source, creating bottlenecks so not all the power reaches the load. Ordinary wires act as antennas, radiating the power into space as radio waves, and in radio receivers can also pick up 
 is the peak voltage along the line
is the peak voltage along the line is the
is the  is the
is the  is the distance along the line
is the distance along the line is time
is time of the line
of the line


 ) or a multiple of it. A
) or a multiple of it. A  ) or a multiple of it.
) or a multiple of it.
 ), or a dipole antenna shorter than a half-wavelength (
), or a dipole antenna shorter than a half-wavelength ( ) will have
) will have 
 . As a result, other resistances in the antenna, the ohmic resistance of metal antenna elements, the ground system if present, and the loading coil, dissipate an increasing fraction of transmitter power as heat. A monopole antenna with an electrical length below .05
. As a result, other resistances in the antenna, the ohmic resistance of metal antenna elements, the ground system if present, and the loading coil, dissipate an increasing fraction of transmitter power as heat. A monopole antenna with an electrical length below .05 ) or very long (
) or very long ( ). Electromagnetics is divided into three regimes or
). Electromagnetics is divided into three regimes or  of the waves: Completely different apparatus is used to conduct and process electromagnetic waves in these different wavelength ranges
of the waves: Completely different apparatus is used to conduct and process electromagnetic waves in these different wavelength ranges

 , the action occurs in the
, the action occurs in the  . So the electrical energy remains in the wires and components as
. So the electrical energy remains in the wires and components as  ,
,  ), as it is in the
), as it is in the  ,
,  , most of the path of the waves is in the
, most of the path of the waves is in the  , absorption,
, absorption, 









 lower than the speed of light
lower than the speed of light