In geometry, it is an unsolved conjecture of Hugo Hadwiger that every simplex can be dissected into orthoschemes, using a number of orthoschemes bounded by a function of the dimension of the simplex. If true, then more generally every convex polytope could be dissected into orthoschemes.
Definitions and statement
In this context, a simplex in -dimensional Euclidean space is the convex hull of points that do not all lie in a common hyperplane. For example, a 2-dimensional simplex is just a triangle (the convex hull of three points in the plane) and a 3-dimensional simplex is a tetrahedron (the convex of four points in three-dimensional space). The points that form the simplex in this way are called its vertices.
An orthoscheme, also called a path simplex, is a special kind of simplex. In it, the vertices can be connected by a path, such that every two edges in the path are at right angles to each other. A two-dimensional orthoscheme is a right triangle. A three-dimensional orthoscheme can be constructed from a cube by finding a path of three edges of the cube that do not all lie on the same square face, and forming the convex hull of the four vertices on this path.

A dissection of a shape (which may be any closed set in Euclidean space) is a representation of as a union of other shapes whose interiors are disjoint from each other. That is, intuitively, the shapes in the union do not overlap, although they may share points on their boundaries. For instance, a cube can be dissected into six three-dimensional orthoschemes. A similar result applies more generally: every hypercube or hyperrectangle in dimensions can be dissected into orthoschemes.
Hadwiger's conjecture is that there is a function such that every -dimensional simplex can be dissected into at most orthoschemes. Hadwiger posed this problem in 1956; it remains unsolved in general, although special cases for small values of are known.
In small dimensions
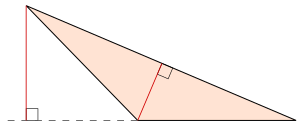
In two dimensions, every triangle can be dissected into at most two right triangles, by dropping an altitude from its widest angle onto its longest edge.
In three dimensions, some tetrahedra can be dissected in a similar way, by dropping an altitude perpendicularly from a vertex to a point in an opposite face, connecting perpendicularly to the sides of the face, and using the three-edge perpendicular paths through and to a side and then to a vertex of the face. However, this does not always work. In particular, there exist tetrahedra for which none of the vertices have altitudes with a foot inside the opposite face. Using a more complicated construction, Lenhard (1960) proved that every tetrahedron can be dissected into at most 12 orthoschemes. Böhm (1980) proved that this is optimal: there exist tetrahedra that cannot be dissected into fewer than 12 orthoschemes. In the same paper, Böhm also generalized Lenhard's result to three-dimensional spherical geometry and three-dimensional hyperbolic geometry.
In four dimensions, at most 500 orthoschemes are needed. In five dimensions, a finite number of orthoschemes is again needed, roughly bounded as at most 12.5 million. Again, this applies to spherical geometry and hyperbolic geometry as well as to Euclidean geometry.
Hadwiger's conjecture remains unproven for all dimensions greater than five.
Consequences
Every convex polytope may be dissected into simplexes. Therefore, if Hadwiger's conjecture is true, every convex polytope would also have a dissection into orthoschemes.
A related result is that every orthoscheme can itself be dissected into or smaller orthoschemes. Therefore, for simplexes that can be partitioned into orthoschemes, their dissections can have arbitrarily large numbers of orthoschemes.
References
- ^ Brandts, Jan; Korotov, Sergey; Křížek, Michal; Šolc, Jakub (2009), "On nonobtuse simplicial partitions" (PDF), SIAM Review, 51 (2): 317–335, Bibcode:2009SIAMR..51..317B, doi:10.1137/060669073, MR 2505583. See in particular Conjecture 23, p. 327.
- ^ Hadwiger, Hugo (1956), "Ungelöste Probleme", Elemente der Mathematik, 11: 109–110
- Lenhard, H.-Chr. (1960), "Zerlegung von Tetraedern in Orthogonaltetraeder", Elemente der Mathematik, 15: 106–107, MR 0116226
- Böhm, Johannes (1980), "Zur vollständigen Zerlegung der euklidischen und nichteuklidischen Tetraeder in Orthogonal-Tetraeder", Martin-Luther-Universität Halle-Wittenberg (9): 29–54, MR 0579516
- Tschirpke, Katrin (1993), "On the dissection of simplices into orthoschemes", Geometriae Dedicata, 46 (3): 313–329, doi:10.1007/BF01263622, MR 1220122
- ^ Tschirpke, Katrin (1994), "The dissection of five-dimensional simplices into orthoschemes", Beiträge zur Algebra und Geometrie, 35 (1): 1–11, MR 1287191
- Debrunner, Hans E. (1990), "Dissecting orthoschemes into orthoschemes", Geometriae Dedicata, 33 (2): 123–152, doi:10.1007/BF00183080, MR 1050606
- Brandts, Jan; Korotov, Sergey; Křížek, Michal (2007), "Dissection of the path-simplex in into path-subsimplices", Linear Algebra and Its Applications, 421 (2–3): 382–393, doi:10.1016/j.laa.2006.10.010, MR 2294350
 -dimensional
-dimensional  points that do not all lie in a common
points that do not all lie in a common  (which may be any
(which may be any  orthoschemes.
orthoschemes.
 such that every
such that every  orthoschemes. Hadwiger posed this problem in 1956; it remains unsolved in general, although special cases for small values of
orthoschemes. Hadwiger posed this problem in 1956; it remains unsolved in general, although special cases for small values of  to a point
to a point  in an opposite face, connecting
in an opposite face, connecting  into
into  path-subsimplices", Linear Algebra and Its Applications, 421 (2–3): 382–393,
path-subsimplices", Linear Algebra and Its Applications, 421 (2–3): 382–393,