In semiconductors, the band gap of a semiconductor can be of two basic types, a direct band gap or an indirect band gap. The minimal-energy state in the conduction band and the maximal-energy state in the valence band are each characterized by a certain crystal momentum (k-vector) in the Brillouin zone. If the k-vectors are different, the material has an "indirect gap". The band gap is called "direct" if the crystal momentum of electrons and holes is the same in both the conduction band and the valence band; an electron can directly emit a photon. In an "indirect" gap, a photon cannot be emitted because the electron must pass through an intermediate state and transfer momentum to the crystal lattice.
Examples of direct bandgap materials include hydrogenated amorphous silicon and some III–V materials such as InAs and GaAs. Indirect bandgap materials include crystalline silicon and Ge. Some III–V materials are indirect bandgap as well, for example AlSb.


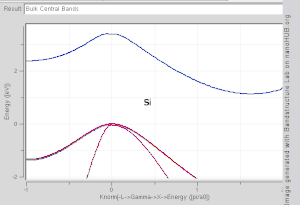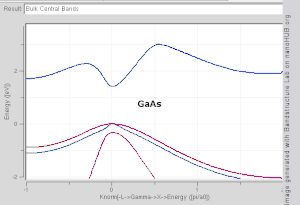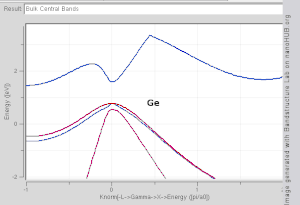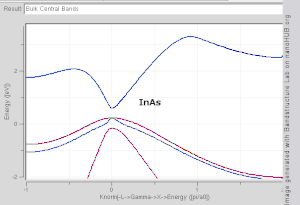
Implications for radiative recombination
See also: Radiative recombinationInteractions among electrons, holes, phonons, photons, and other particles are required to satisfy conservation of energy and crystal momentum (i.e., conservation of total k-vector). A photon with an energy near a semiconductor band gap has almost zero momentum. One important process is called radiative recombination, where an electron in the conduction band annihilates a hole in the valence band, releasing the excess energy as a photon. This is possible in a direct band gap semiconductor if the electron has a k-vector near the conduction band minimum (the hole will share the same k-vector), but not possible in an indirect band gap semiconductor, as photons cannot carry crystal momentum, and thus conservation of crystal momentum would be violated. For radiative recombination to occur in an indirect band gap material, the process must also involve the absorption or emission of a phonon, where the phonon momentum equals the difference between the electron and hole momentum. It can also, instead, involve a crystallographic defect, which performs essentially the same role. The involvement of the phonon makes this process much less likely to occur in a given span of time, which is why radiative recombination is far slower in indirect band gap materials than direct band gap ones. This is why light-emitting and laser diodes are almost always made of direct band gap materials, and not indirect band gap ones like silicon.
The fact that radiative recombination is slow in indirect band gap materials also means that, under most circumstances, radiative recombinations will be a small proportion of total recombinations, with most recombinations being non-radiative, taking place at point defects or at grain boundaries. However, if the excited electrons are prevented from reaching these recombination places, they have no choice but to eventually fall back into the valence band by radiative recombination. This can be done by creating a dislocation loop in the material. At the edge of the loop, the planes above and beneath the "dislocation disk" are pulled apart, creating a negative pressure, which raises the energy of the conduction band substantially, with the result that the electrons cannot pass this edge. Provided that the area directly above the dislocation loop is defect-free (no non-radiative recombination possible), the electrons will fall back into the valence shell by radiative recombination, thus emitting light. This is the principle on which "DELEDs" (Dislocation Engineered LEDs) are based.
Implications for light absorption
The exact reverse of radiative recombination is light absorption. For the same reason as above, light with a photon energy close to the band gap can penetrate much farther before being absorbed in an indirect band gap material than a direct band gap one (at least insofar as the light absorption is due to exciting electrons across the band gap).
This fact is very important for photovoltaics (solar cells). Crystalline silicon is the most common solar-cell substrate material, despite the fact that it is indirect-gap and therefore does not absorb light very well. As such, they are typically hundreds of microns thick; thinner wafers would allow much of the light (particularly in longer wavelengths) to simply pass through. By comparison, thin-film solar cells are made of direct band gap materials (such as amorphous silicon, CdTe, CIGS or CZTS), which absorb the light in a much thinner region, and consequently can be made with a very thin active layer (often less than 1 micron thick).
The absorption spectrum of an indirect band gap material usually depends more on temperature than that of a direct material, because at low temperatures there are fewer phonons, and therefore it is less likely that a photon and phonon can be simultaneously absorbed to create an indirect transition. For example, silicon is opaque to visible light at room temperature, but transparent to red light at liquid helium temperatures, because red photons can only be absorbed in an indirect transition.
Formula for absorption
A common and simple method for determining whether a band gap is direct or indirect uses absorption spectroscopy. By plotting certain powers of the absorption coefficient against photon energy, one can normally tell both what value the band gap is, and whether or not it is direct.
For a direct band gap, the absorption coefficient is related to light frequency according to the following formula:
- , with
where:
- is the absorption coefficient, a function of light frequency
- is light frequency
- is the Planck constant ( is the energy of a photon with frequency )
- is the reduced Planck constant ()
- is the band gap energy
- is a certain constant, with formula above
- , where and are the effective masses of the electron and hole, respectively ( is called a "reduced mass")
- is the elementary charge
- is the (real) index of refraction
- is the vacuum permittivity
- is the vacuum wavelength for light of frequency
- is a "matrix element", with units of length and typical value the same order of magnitude as the lattice constant.
This formula is valid only for light with photon energy larger, but not too much larger, than the band gap (more specifically, this formula assumes the bands are approximately parabolic), and ignores all other sources of absorption other than the band-to-band absorption in question, as well as the electrical attraction between the newly created electron and hole (see exciton). It is also invalid in the case that the direct transition is forbidden, or in the case that many of the valence band states are empty or conduction band states are full.
On the other hand, for an indirect band gap, the formula is:
where:
- is the energy of the phonon that assists in the transition
- is the Boltzmann constant
- is the thermodynamic temperature
This formula involves the same approximations mentioned above.
Therefore, if a plot of versus forms a straight line, it can normally be inferred that there is a direct band gap, measurable by extrapolating the straight line to the axis. On the other hand, if a plot of versus forms a straight line, it can normally be inferred that there is an indirect band gap, measurable by extrapolating the straight line to the axis (assuming ).
Other aspects
In some materials with an indirect gap, the value of the gap is negative. The top of the valence band is higher than the bottom of the conduction band in energy. Such materials are known as semimetals.
See also
References
- Optoelectronics, by E. Rosencher, 2002, equation (7.25).
- Pankove has the same equation, but with an apparently different prefactor . However, in the Pankove version, the units / dimensional analysis appears not to work out.
- ^ J.I. Pankove, Optical Processes in Semiconductors. Dover, 1971.
External links
- B. Van Zeghbroeck's Principles of Semiconductor Devices Archived 2009-01-22 at the Wayback Machine at Electrical and Computer Engineering Department of University of Colorado at Boulder
 is related to light frequency according to the following formula:
is related to light frequency according to the following formula:
 , with
, with 
 is light frequency
is light frequency is the
is the  is the energy of a
is the energy of a  is the
is the  )
) is the band gap energy
is the band gap energy is a certain constant, with formula above
is a certain constant, with formula above , where
, where  and
and  are the
are the  is called a "
is called a " is the
is the  is the (real)
is the (real)  is the
is the  is the vacuum wavelength for light of frequency
is the vacuum wavelength for light of frequency  is a "matrix element", with units of length and typical value the same order of magnitude as the
is a "matrix element", with units of length and typical value the same order of magnitude as the 
 is the energy of the
is the energy of the  is the
is the  is the
is the  forms a straight line, it can normally be inferred that there is a direct band gap, measurable by extrapolating the straight line to the
forms a straight line, it can normally be inferred that there is a direct band gap, measurable by extrapolating the straight line to the  axis. On the other hand, if a plot of
axis. On the other hand, if a plot of  forms a straight line, it can normally be inferred that there is an indirect band gap, measurable by extrapolating the straight line to the
forms a straight line, it can normally be inferred that there is an indirect band gap, measurable by extrapolating the straight line to the  ).
).