In mathematics, a cube root of a number x is a number y that has the given number as its third power; that is The number of cube roots of a number depends on the number system that is considered.
Every nonzero real number x has exactly one real cube root that is denoted and called the real cube root of x or simply the cube root of x in contexts where complex numbers are not considered. For example, the real cube roots of 8 and −8 are respectively 2 and −2. The real cube root of an integer or of a rational number is generally not a rational number, neither a constructible number.
Every nonzero real of complex number has exactly three cube roots that are complex numbers. If the number is real, one of the cube roots is real and the two other are nonreal complex conjugate numbers. Otherwise, the three cube roots are all nonreal. For example, the real cube root of 8 is 2 and the other cube roots of 8 are and . The three cube roots of −27i are and The number zero has a unique cube root, which is zero itself.
In some contexts, it is convenient to choose a particular cube root for every complex number. This cube root is called the principal cube root and is the cube root with the largest real part. In the case of negative real numbers, the two nonreal roots share the same largest real part, and the principal cube root is the one with positive imaginary part; so, it is different from the real cube root. If y is any cube root of the complex number x, the other cube roots are and
In an algebraically closed field of characteristic different from three, every nonzero element has exactly three cube roots, which can be obtained from any of them by multiplying it by either root of the polynomial In an algebraically closed field of characteristic three, every element has exactly one cube root.
In other number systems or other algebraic structures, a number or element may have more than three cube roots. For example, in the quaternions, a real number has infinitely many cube roots.


Definition
The cube roots of a number x are the numbers y which satisfy the equation
Properties
Real numbers
For any real number x, there is exactly one real number y such that . Indeeed, the cube function is increasing, so does not give the same result for two different inputs, and covers all real numbers. In other words, it is a bijection or one-to-one correspondence.
That is, one can define the cube root of a real number as its unique cube root that is also real. With this definition, the cube root of a negative number is a negative number.
However this definition may be confusing when real numbers are considered as specific complex numbers, since, in this case the cube root is generally defined as the principal cube root, and the principal cube root of a negative real number is not real.
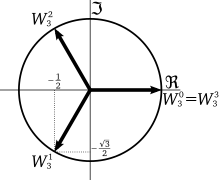
If x and y are allowed to be complex, then there are three solutions (if x is non-zero) and so x has three cube roots. A real number has one real cube root and two further cube roots which form a complex conjugate pair. For instance, the cube roots of 1 are:
The last two of these roots lead to a relationship between all roots of any real or complex number. If a number is one cube root of a particular real or complex number, the other two cube roots can be found by multiplying that cube root by one or the other of the two complex cube roots of 1.
Complex numbers


For complex numbers, the principal cube root is usually defined as the cube root that has the greatest real part, or, equivalently, the cube root whose argument has the least absolute value. It is related to the principal value of the natural logarithm by the formula
If we write x as
where r is a non-negative real number and lies in the range
- ,
then the principal complex cube root is
This means that in polar coordinates, we are taking the cube root of the radius and dividing the polar angle by three in order to define a cube root. With this definition, the principal cube root of a negative number is a complex number, and for instance will not be −2, but rather
This difficulty can also be solved by considering the cube root as a multivalued function: if we write the original complex number x in three equivalent forms, namely

The principal complex cube roots of these three forms are then respectively
Unless x = 0, these three complex numbers are distinct, even though the three representations of x were equivalent. For example, may then be calculated to be −2, , or .
This is related with the concept of monodromy: if one follows by continuity the function cube root along a closed path around zero, after a turn the value of the cube root is multiplied (or divided) by
Impossibility of compass-and-straightedge construction
Cube roots arise in the problem of finding an angle whose measure is one third that of a given angle (angle trisection) and in the problem of finding the edge of a cube whose volume is twice that of a cube with a given edge (doubling the cube). In 1837 Pierre Wantzel proved that neither of these can be done with a compass-and-straightedge construction.
Numerical methods
Newton's method is an iterative method that can be used to calculate the cube root. For real floating-point numbers this method reduces to the following iterative algorithm to produce successively better approximations of the cube root of a:
The method is simply averaging three factors chosen such that
at each iteration.
Halley's method improves upon this with an algorithm that converges more quickly with each iteration, albeit with more work per iteration:
This converges cubically, so two iterations do as much work as three iterations of Newton's method. Each iteration of Newton's method costs two multiplications, one addition and one division, assuming that 1/3a is precomputed, so three iterations plus the precomputation require seven multiplications, three additions, and three divisions.
Each iteration of Halley's method requires three multiplications, three additions, and one division, so two iterations cost six multiplications, six additions, and two divisions. Thus, Halley's method has the potential to be faster if one division is more expensive than three additions.
With either method a poor initial approximation of x0 can give very poor algorithm performance, and coming up with a good initial approximation is somewhat of a black art. Some implementations manipulate the exponent bits of the floating-point number; i.e. they arrive at an initial approximation by dividing the exponent by 3.
Also useful is this generalized continued fraction, based on the nth root method:
If x is a good first approximation to the cube root of a and , then:
The second equation combines each pair of fractions from the first into a single fraction, thus doubling the speed of convergence.
Appearance in solutions of third and fourth degree equations
Cubic equations, which are polynomial equations of the third degree (meaning the highest power of the unknown is 3) can always be solved for their three solutions in terms of cube roots and square roots (although simpler expressions only in terms of square roots exist for all three solutions, if at least one of them is a rational number). If two of the solutions are complex numbers, then all three solution expressions involve the real cube root of a real number, while if all three solutions are real numbers then they may be expressed in terms of the complex cube root of a complex number.
Quartic equations can also be solved in terms of cube roots and square roots.
History
The calculation of cube roots can be traced back to Babylonian mathematicians from as early as 1800 BCE. In the fourth century BCE Plato posed the problem of doubling the cube, which required a compass-and-straightedge construction of the edge of a cube with twice the volume of a given cube; this required the construction, now known to be impossible, of the length .
A method for extracting cube roots appears in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the second century BCE and commented on by Liu Hui in the third century CE. The Greek mathematician Hero of Alexandria devised a method for calculating cube roots in the first century CE. His formula is again mentioned by Eutokios in a commentary on Archimedes. In 499 CE Aryabhata, a mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave a method for finding the cube root of numbers having many digits in the Aryabhatiya (section 2.5).
See also
- Methods of computing square roots
- List of polynomial topics
- Nth root
- Square root
- Nested radical
- Root of unity
References
- ^ "In Search of a Fast Cube Root". metamerist.com. 2008. Archived from the original on 27 December 2013.
- Saggs, H. W. F. (1989). Civilization Before Greece and Rome. Yale University Press. p. 227. ISBN 978-0-300-05031-8.
- Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 213. ISBN 978-0-19-853936-0.
- Smyly, J. Gilbart (1920). "Heron's Formula for Cube Root". Hermathena. 19 (42). Trinity College Dublin: 64–67. JSTOR 23037103.
- Aryabhatiya Archived 15 August 2011 at archive.today Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p. 62, ISBN 978-81-7434-480-9
External links
- Cube root calculator reduces any number to simplest radical form
- Computing the Cube Root, Ken Turkowski, Apple Technical Report #KT-32, 1998. Includes C source code.
- Weisstein, Eric W. "Cube Root". MathWorld.
 The number of cube roots of a number depends on the
The number of cube roots of a number depends on the  and called the real cube root of x or simply the cube root of x in contexts where
and called the real cube root of x or simply the cube root of x in contexts where  and
and  . The three cube roots of −27i are
. The three cube roots of −27i are
 and
and  The number zero has a unique cube root, which is zero itself.
The number zero has a unique cube root, which is zero itself.
 and
and 
 In an algebraically closed field of characteristic three, every element has exactly one cube root.
In an algebraically closed field of characteristic three, every element has exactly one cube root.

 . Indeeed, the
. Indeeed, the 


 lies in the range
lies in the range
 ,
,
 will not be −2, but rather
will not be −2, but rather 


 .
.




 , then:
, then:


 .
.