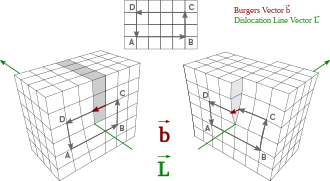
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as glide or slip. The crystalline order is restored on either side of a glide dislocation but the atoms on one side have moved by one position. The crystalline order is not fully restored with a partial dislocation. A dislocation defines the boundary between slipped and unslipped regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plastic deformation of a material occurs by the creation and movement of many dislocations. The number and arrangement of dislocations influences many of the properties of materials.
The two primary types of dislocations are sessile dislocations which are immobile and glissile dislocations which are mobile. Examples of sessile dislocations are the stair-rod dislocation and the Lomer–Cottrell junction. The two main types of mobile dislocations are edge and screw dislocations.
Edge dislocations can be visualized as being caused by the termination of a plane of atoms in the middle of a crystal. In such a case, the surrounding planes are not straight, but instead bend around the edge of the terminating plane so that the crystal structure is perfectly ordered on either side. This phenomenon is analogous to half of a piece of paper inserted into a stack of paper, where the defect in the stack is noticeable only at the edge of the half sheet.
The theory describing the elastic fields of the defects was originally developed by Vito Volterra in 1907. In 1934, Egon Orowan, Michael Polanyi and G. I. Taylor, proposed that the low stresses observed to produce plastic deformation compared to theoretical predictions at the time could be explained in terms of the theory of dislocations.
History
The theory describing the elastic fields of the defects was originally developed by Vito Volterra in 1907. The term 'dislocation' referring to a defect on the atomic scale was coined by G. I. Taylor in 1934.
Prior to the 1930s, one of the enduring challenges of materials science was to explain plasticity in microscopic terms. A simplistic attempt to calculate the shear stress at which neighbouring atomic planes slip over each other in a perfect crystal suggests that, for a material with shear modulus , shear strength is given approximately by:
The shear modulus in metals is typically within the range 20 000 to 150 000 MPa indicating a predicted shear stress of 3 000 to 24 000 MPa. This was difficult to reconcile with measured shear stresses in the range of 0.5 to 10 MPa.
In 1934, Egon Orowan, Michael Polanyi and G. I. Taylor, independently proposed that plastic deformation could be explained in terms of the theory of dislocations. Dislocations can move if the atoms from one of the surrounding planes break their bonds and rebond with the atoms at the terminating edge. In effect, a half plane of atoms is moved in response to shear stress by breaking and reforming a line of bonds, one (or a few) at a time. The energy required to break a row of bonds is far less than that required to break all the bonds on an entire plane of atoms at once. Even this simple model of the force required to move a dislocation shows that plasticity is possible at much lower stresses than in a perfect crystal. In many materials, particularly ductile materials, dislocations are the "carrier" of plastic deformation, and the energy required to move them is less than the energy required to fracture the material.
Mechanisms
A dislocation is a linear crystallographic defect or irregularity within a crystal structure which contains an abrupt change in the arrangement of atoms. The crystalline order is restored on either side of a dislocation but the atoms on one side have moved or slipped. Dislocations define the boundary between slipped and unslipped regions of material and cannot end within a lattice and must either extend to a free edge or form a loop within the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms in the lattice which is called the Burgers vector. The Burgers vector of a dislocation remains constant even though the shape of the dislocation may change.
A variety of dislocation types exist, with mobile dislocations known as glissile and immobile dislocations called sessile. The movement of mobile dislocations allow atoms to slide over each other at low stress levels and is known as glide or slip. The movement of dislocations may be enhanced or hindered by the presence of other elements within the crystal and over time, these elements may diffuse to the dislocation forming a Cottrell atmosphere. The pinning and breakaway from these elements explains some of the unusual yielding behavior seen with steels. The interaction of hydrogen with dislocations is one of the mechanisms proposed to explain hydrogen embrittlement.
Dislocations behave as though they are a distinct entity within a crystalline material where some types of dislocation can move through the material bending, flexing and changing shape and interacting with other dislocations and features within the crystal. Dislocations are generated by deforming a crystalline material such as metals, which can cause them to initiate from surfaces, particularly at stress concentrations or within the material at defects and grain boundaries. The number and arrangement of dislocations give rise to many of the properties of metals such as ductility, hardness and yield strength. Heat treatment, alloy content and cold working can change the number and arrangement of the dislocation population and how they move and interact in order to create useful properties.
Generating dislocations
When metals are subjected to cold working (deformation at temperatures which are relatively low as compared to the material's absolute melting temperature, i.e., typically less than ) the dislocation density increases due to the formation of new dislocations. The consequent increasing overlap between the strain fields of adjacent dislocations gradually increases the resistance to further dislocation motion. This causes a hardening of the metal as deformation progresses. This effect is known as strain hardening or work hardening.
Dislocation density in a material can be increased by plastic deformation by the following relationship:
- .
Since the dislocation density increases with plastic deformation, a mechanism for the creation of dislocations must be activated in the material. Three mechanisms for dislocation formation are homogeneous nucleation, grain boundary initiation, and interfaces between the lattice and the surface, precipitates, dispersed phases, or reinforcing fibers.
Homogeneous nucleation
The creation of a dislocation by homogeneous nucleation is a result of the rupture of the atomic bonds along a line in the lattice. A plane in the lattice is sheared, resulting in 2 oppositely faced half planes or dislocations. These dislocations move away from each other through the lattice. Since homogeneous nucleation forms dislocations from perfect crystals and requires the simultaneous breaking of many bonds, the energy required for homogeneous nucleation is high. For instance, the stress required for homogeneous nucleation in copper has been shown to be , where is the shear modulus of copper (46 GPa). Solving for , we see that the required stress is 3.4 GPa, which is very close to the theoretical strength of the crystal. Therefore, in conventional deformation homogeneous nucleation requires a concentrated stress, and is very unlikely. Grain boundary initiation and interface interaction are more common sources of dislocations.
Irregularities at the grain boundaries in materials can produce dislocations which propagate into the grain. The steps and ledges at the grain boundary are an important source of dislocations in the early stages of plastic deformation.
Frank–Read source
Main article: Frank–Read sourceThe Frank–Read source is a mechanism that is able to produce a stream of dislocations from a pinned segment of a dislocation. Stress bows the dislocation segment, expanding until it creates a dislocation loop that breaks free from the source.
Surfaces
The surface of a crystal can produce dislocations in the crystal. Due to the small steps on the surface of most crystals, stress in some regions on the surface is much larger than the average stress in the lattice. This stress leads to dislocations. The dislocations are then propagated into the lattice in the same manner as in grain boundary initiation. In single crystals, the majority of dislocations are formed at the surface. The dislocation density 200 micrometres into the surface of a material has been shown to be six times higher than the density in the bulk. However, in polycrystalline materials the surface sources do not have a major effect because most grains are not in contact with the surface.
Interfaces
The interface between a metal and an oxide can greatly increase the number of dislocations created. The oxide layer puts the surface of the metal in tension because the oxygen atoms squeeze into the lattice, and the oxygen atoms are under compression. This greatly increases the stress on the surface of the metal and consequently the amount of dislocations formed at the surface. The increased amount of stress on the surface steps results in an increase in dislocations formed and emitted from the interface.
Dislocations may also form and remain in the interface plane between two crystals. This occurs when the lattice spacing of the two crystals do not match, resulting in a misfit of the lattices at the interface. The stress caused by the lattice misfit is released by forming regularly spaced misfit dislocations. Misfit dislocations are edge dislocations with the dislocation line in the interface plane and the Burgers vector in the direction of the interface normal. Interfaces with misfit dislocations may form e.g. as a result of epitaxial crystal growth on a substrate.
Irradiation
Dislocation loops may form in the damage created by energetic irradiation. A prismatic dislocation loop can be understood as an extra (or missing) collapsed disk of atoms, and can form when interstitial atoms or vacancies cluster together. This may happen directly as a result of single or multiple collision cascades, which results in locally high densities of interstitial atoms and vacancies. In most metals, prismatic dislocation loops are the energetically most preferred clusters of self-interstitial atoms.
Interaction and arrangement
Geometrically necessary dislocations
Main article: Geometrically necessary dislocationsGeometrically necessary dislocations are arrangements of dislocations that can accommodate a limited degree of plastic bending in a crystalline material. Tangles of dislocations are found at the early stage of deformation and appear as non well-defined boundaries; the process of dynamic recovery leads eventually to the formation of a cellular structure containing boundaries with misorientation lower than 15° (low angle grain boundaries).
Pinning
Adding pinning points that inhibit the motion of dislocations, such as alloying elements, can introduce stress fields that ultimately strengthen the material by requiring a higher applied stress to overcome the pinning stress and continue dislocation motion.
The effects of strain hardening by accumulation of dislocations and the grain structure formed at high strain can be removed by appropriate heat treatment (annealing) which promotes the recovery and subsequent recrystallization of the material.
The combined processing techniques of work hardening and annealing allow for control over dislocation density, the degree of dislocation entanglement, and ultimately the yield strength of the material.
Persistent slip bands
Main article: Persistent slip bandsRepeated cycling of a material can lead to the generation and bunching of dislocations surrounded by regions that are relatively dislocation free. This pattern forms a ladder like structure known as a persistent slip bands (PSB). PSB's are so-called, because they leave marks on the surface of metals that even when removed by polishing, return at the same place with continued cycling.
PSB walls are predominately made up of edge dislocations. In between the walls, plasticity is transmitted by screw dislocations.
Where PSB's meet the surface, extrusions and intrusions form, which under repeated cyclic loading, can lead to the initiation of a fatigue crack.
Movement
Main articles: Slip (materials science) and Dislocation creepGlide
Dislocations can slip in planes containing both the dislocation line and the Burgers vector, the so called glide plane. For a screw dislocation, the dislocation line and the Burgers vector are parallel, so the dislocation may slip in any plane containing the dislocation. For an edge dislocation, the dislocation and the Burgers vector are perpendicular, so there is one plane in which the dislocation can slip.
Climb
Dislocation climb is an alternative mechanism of dislocation motion that allows an edge dislocation to move out of its slip plane. The driving force for dislocation climb is the movement of vacancies through a crystal lattice. If a vacancy moves next to the boundary of the extra half plane of atoms that forms an edge dislocation, the atom in the half plane closest to the vacancy can jump and fill the vacancy. This atom shift moves the vacancy in line with the half plane of atoms, causing a shift, or positive climb, of the dislocation. The process of a vacancy being absorbed at the boundary of a half plane of atoms, rather than created, is known as negative climb. Since dislocation climb results from individual atoms jumping into vacancies, climb occurs in single atom diameter increments.
During positive climb, the crystal shrinks in the direction perpendicular to the extra half plane of atoms because atoms are being removed from the half plane. Since negative climb involves an addition of atoms to the half plane, the crystal grows in the direction perpendicular to the half plane. Therefore, compressive stress in the direction perpendicular to the half plane promotes positive climb, while tensile stress promotes negative climb. This is one main difference between slip and climb, since slip is caused by only shear stress.
One additional difference between dislocation slip and climb is the temperature dependence. Climb occurs much more rapidly at high temperatures than low temperatures due to an increase in vacancy motion. Slip, on the other hand, has only a small dependence on temperature.
Dislocation avalanches
Main article: Dislocation avalanchesDislocation avalanches occur when multiple simultaneous movement of dislocations occur.
Dislocation Velocity
Dislocation velocity is largely dependent upon shear stress and temperature, and can often be fit using a power law function:
where is a material constant, is the applied shear stress, is a constant that decreases with increasing temperature. Increased shear stress will increase the dislocation velocity, while increased temperature will typically decrease the dislocation velocity. Greater phonon scattering at higher temperatures is hypothesized to be responsible for increased damping forces which slow the dislocation movement.
Geometry

Two main types of mobile dislocations exist: edge and screw. Dislocations found in real materials are typically mixed, meaning that they have characteristics of both.
Edge
A crystalline material consists of a regular array of atoms, arranged into lattice planes. An edge dislocation is a defect where an extra half-plane of atoms is introduced midway through the crystal, distorting nearby planes of atoms. When enough force is applied from one side of the crystal structure, this extra plane passes through planes of atoms breaking and joining bonds with them until it reaches the grain boundary. The dislocation has two properties, a line direction, which is the direction running along the bottom of the extra half plane, and the Burgers vector which describes the magnitude and direction of distortion to the lattice. In an edge dislocation, the Burgers vector is perpendicular to the line direction.
The stresses caused by an edge dislocation are complex due to its inherent asymmetry. These stresses are described by three equations:
where is the shear modulus of the material, is the Burgers vector, is Poisson's ratio and and are coordinates.
These equations suggest a vertically oriented dumbbell of stresses surrounding the dislocation, with compression experienced by the atoms near the "extra" plane, and tension experienced by those atoms near the "missing" plane.
Screw
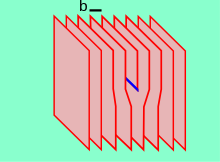
A screw dislocation can be visualized by cutting a crystal along a plane and slipping one half across the other by a lattice vector, the halves fitting back together without leaving a defect. If the cut only goes part way through the crystal, and then slipped, the boundary of the cut is a screw dislocation. It comprises a structure in which a helical path is traced around the linear defect (dislocation line) by the atomic planes in the crystal lattice. In pure screw dislocations, the Burgers vector is parallel to the line direction. An array of screw dislocations can cause what is known as a twist boundary. In a twist boundary, the misalignment between adjacent crystal grains occurs due to the cumulative effect of screw dislocations within the material. These dislocations cause a rotational misorientation between the adjacent grains, leading to a twist-like deformation along the boundary. Twist boundaries can significantly influence the mechanical and electrical properties of materials, affecting phenomena such as grain boundary sliding, creep, and fracture behavior The stresses caused by a screw dislocation are less complex than those of an edge dislocation and need only one equation, as symmetry allows one radial coordinate to be used:
where is the shear modulus of the material, is the Burgers vector, and is a radial coordinate. This equation suggests a long cylinder of stress radiating outward from the cylinder and decreasing with distance. This simple model results in an infinite value for the core of the dislocation at and so it is only valid for stresses outside of the core of the dislocation. If the Burgers vector is very large, the core may actually be empty resulting in a micropipe, as commonly observed in silicon carbide.
Mixed
In many materials, dislocations are found where the line direction and Burgers vector are neither perpendicular nor parallel and these dislocations are called mixed dislocations, consisting of both screw and edge character. They are characterized by , the angle between the line direction and Burgers vector, where for pure edge dislocations and for screw dislocations.
Partial
Main article: Partial dislocationsPartial dislocations leave behind a stacking fault. Two types of partial dislocation are the Frank partial dislocation which is sessile and the Shockley partial dislocation which is glissile.
A Frank partial dislocation is formed by inserting or removing a layer of atoms on the {111} plane which is then bounded by the Frank partial. Removal of a close packed layer is known as an intrinsic stacking fault and inserting a layer is known as an extrinsic stacking fault. The Burgers vector is normal to the {111} glide plane so the dislocation cannot glide and can only move through climb.
In order to lower the overall energy of the lattice, edge and screw dislocations typically disassociate into a stacking fault bounded by two Shockley partial dislocations. The width of this stacking-fault region is proportional to the stacking-fault energy of the material. The combined effect is known as an extended dislocation and is able to glide as a unit. However, dissociated screw dislocations must recombine before they can cross slip, making it difficult for these dislocations to move around barriers. Materials with low stacking-fault energies have the greatest dislocation dissociation and are therefore more readily cold worked.
Stair-rod and the Lomer–Cottrell junction
If two glide dislocations that lie on different {111} planes split into Shockley partials and intersect, they will produce a stair-rod dislocation with a Lomer-Cottrell dislocation at its apex. It is called a stair-rod because it is analogous to the rod that keeps carpet in-place on a stair.
Jog
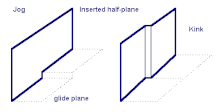
A Jog describes the steps of a dislocation line that are not in the glide plane of a crystal structure. A dislocation line is rarely uniformly straight, often containing many curves and steps that can impede or facilitate dislocation movement by acting as pinpoints or nucleation points respectively. Because jogs are out of the glide plane, under shear they cannot move by glide (movement along the glide plane). They instead must rely on vacancy diffusion facilitated climb to move through the lattice. Away from the melting point of a material, vacancy diffusion is a slow process, so jogs act as immobile barriers at room temperature for most metals.
Jogs typically form when two non-parallel dislocations cross during slip. The presence of jogs in a material increases its yield strength by preventing easy glide of dislocations. A pair of immobile jogs in a dislocation will act as a Frank–Read source under shear, increasing the overall dislocation density of a material. When a material's yield strength is increased via dislocation density increase, particularly when done by mechanical work, it is called work hardening. At high temperatures, vacancy facilitated movement of jogs becomes a much faster process, diminishing their overall effectiveness in impeding dislocation movement.
Kink
Main article: Kink (materials science)Kinks are steps in a dislocation line parallel to glide planes. Unlike jogs, they facilitate glide by acting as a nucleation point for dislocation movement. The lateral spreading of a kink from the nucleation point allows for forward propagation of the dislocation while only moving a few atoms at a time, reducing the overall energy barrier to slip.
Example in two dimensions (2D)

In two dimensions (2D) only the edge dislocations exist, which play a central role in melting of 2D crystals, but not the screw dislocation. Those dislocations are topological point defects which implies that they cannot be created isolated by an affine transformation without cutting the hexagonal crystal up to infinity (or at least up to its border). They can only be created in pairs with antiparallel Burgers vector. If a lot of dislocations are e. g. thermally excited, the discrete translational order of the crystal is destroyed. Simultaneously, the shear modulus and the Young's modulus disappear, which implies that the crystal is molten to a fluid phase. The orientational order is not yet destroyed (as indicated by lattice lines in one direction) and one finds - very similar to liquid crystals - a fluid phase with typically a six-folded director field. This so-called hexatic phase still has an orientational stiffness. The isotropic fluid phase appears, if the dislocations dissociate into isolated five-folded and seven-folded disclinations. This two step melting is described within the so-called Kosterlitz-Thouless-Halperin-Nelson-Young-theory (KTHNY theory), based on two transitions of Kosterlitz-Thouless-type.
Observation
Transmission electron microscopy (TEM)


Transmission electron microscopy can be used to observe dislocations within the microstructure of the material. Thin foils of material are prepared to render them transparent to the electron beam of the microscope. The electron beam undergoes diffraction by the regular crystal lattice planes into a diffraction pattern and contrast is generated in the image by this diffraction (as well as by thickness variations, varying strain, and other mechanisms). Dislocations have different local atomic structure and produce a strain field, and therefore will cause the electrons in the microscope to scatter in different ways. Note the characteristic 'wiggly' contrast of the dislocation lines as they pass through the thickness of the material in the figure (dislocations cannot end in a crystal, and these dislocations are terminating at the surfaces since the image is a 2D projection).
Dislocations do not have random structures, the local atomic structure of a dislocation is determined by the Burgers vector. One very useful application of the TEM in dislocation imaging is the ability to experimentally determine the Burgers vector. Determination of the Burgers vector is achieved by what is known as ("g dot b") analysis. When performing dark field microscopy with the TEM, a diffracted spot is selected to form the image (as mentioned before, lattice planes diffract the beam into spots), and the image is formed using only electrons that were diffracted by the plane responsible for that diffraction spot. The vector in the diffraction pattern from the transmitted spot to the diffracted spot is the vector. The contrast of a dislocation is scaled by a factor of the dot product of this vector and the Burgers vector (). As a result, if the Burgers vector and vector are perpendicular, there will be no signal from the dislocation and the dislocation will not appear at all in the image. Therefore, by examining different dark field images formed from spots with different g vectors, the Burgers vector can be determined.
Other methods

Field ion microscopy and atom probe techniques offer methods of producing much higher magnifications (typically 3 million times and above) and permit the observation of dislocations at an atomic level. Where surface relief can be resolved to the level of an atomic step, screw dislocations appear as distinctive spiral features – thus revealing an important mechanism of crystal growth: where there is a surface step, atoms can more easily add to the crystal, and the surface step associated with a screw dislocation is never destroyed no matter how many atoms are added to it.
Chemical etching
When a dislocation line intersects the surface of a metallic material, the associated strain field locally increases the relative susceptibility of the material to acid etching and an etch pit of regular geometrical format results. In this way, dislocations in silicon, for example, can be observed indirectly using an interference microscope. Crystal orientation can be determined by the shape of the etch pits associated with the dislocations.
If the material is deformed and repeatedly re-etched, a series of etch pits can be produced which effectively trace the movement of the dislocation in question.
Dislocation forces
Forces on dislocations
Dislocation motion as a result of external stress on a crystal lattice can be described using virtual internal forces which act perpendicular to the dislocation line. The Peach-Koehler equation can be used to calculate the force per unit length on a dislocation as a function of the Burgers vector, , stress, , and the sense vector, .
The force per unit length of dislocation is a function of the general state of stress, , and the sense vector, .
The components of the stress field can be obtained from the Burgers vector, normal stresses, , and shear stresses, .
Forces between dislocations
The force between dislocations can be derived from the energy of interactions of the dislocations, . The work done by displacing cut faces parallel to a chosen axis that creates one dislocation in the stress field of another displacement. For the and directions:
The forces are then found by taking the derivatives.
Free surface forces
Dislocations will also tend to move towards free surfaces due to the lower strain energy. This fictitious force can be expressed for a screw dislocation with the component equal to zero as:
where is the distance from free surface in the direction. The force for an edge dislocation with can be expressed as:
References
- ^ Hull, D.; Bacon, D. J. (2001). Introduction to dislocations (4th ed.). Butterworth-Heinemann. doi:10.1016/B978-0-7506-4681-9.X5000-7. ISBN 978-0-7506-4681-9.
- Anderson, Peter M.; Hirth, John Price; Lothe, Jens (2017). Theory of Dislocations (Third ed.). New York, NY: Cambridge University Press. ISBN 978-0-521-86436-7. OCLC 950750996.
- ^ "Dislocations in FCC materials". 2014-05-24. Retrieved 2019-11-08.
- Vito Volterra (1907) "Sur l'équilibre des corps élastiques multiplement connexes", Annales Scientifiques de l'École Normale Supérieure, Vol. 24, pp. 401–517
- G. I. Taylor (1934). "The Mechanism of Plastic Deformation of Crystals. Part I. Theoretical". Proceedings of the Royal Society of London. Series A. 145 (855): 362–87. Bibcode:1934RSPSA.145..362T. doi:10.1098/rspa.1934.0106. JSTOR 2935509.
- Marc André Meyers, Krishan Kumar Chawla (1999) Mechanical Behaviors of Materials. Prentice Hall, pp. 228–31, ISBN 0132628171.
- Schober, T.; Balluffi, R. W. (1970-01-01). "Quantitative observation of misfit dislocation arrays in low and high angle twist grain boundaries". The Philosophical Magazine. 21 (169): 109–123. Bibcode:1970PMag...21..109S. doi:10.1080/14786437008238400. ISSN 0031-8086.
- Eyre, B. L. (February 1973). "Transmission electron microscope studies of point defect clusters in fcc and bcc metals". Journal of Physics F: Metal Physics. 3 (2): 422–470. Bibcode:1973JPhF....3..422E. doi:10.1088/0305-4608/3/2/009. ISSN 0305-4608.
- Masters, B. C. (1965-05-01). "Dislocation loops in irradiated iron". The Philosophical Magazine. 11 (113): 881–893. Bibcode:1965PMag...11..881M. doi:10.1080/14786436508223952. ISSN 0031-8086. S2CID 4205189.
- Kirk, M. A.; Robertson, I. M.; Jenkins, M. L.; English, C. A.; Black, T. J.; Vetrano, J. S. (1987-06-01). "The collapse of defect cascades to dislocation loops". Journal of Nuclear Materials. 149 (1): 21–28. Bibcode:1987JNuM..149...21K. doi:10.1016/0022-3115(87)90494-6. ISSN 0022-3115.
- ^ Suresh, S. (2004). Fatigue of Materials. Cambridge University Press. ISBN 978-0-521-57046-6.
- Forsythe, P. J. E. (1953). "Exudation of material from slip bands at the surface of fatigued crystals of an aluminium-copper alloy". Nature. 171 (4343): 172–173. Bibcode:1953Natur.171..172F. doi:10.1038/171172a0. S2CID 4268548.
- Grundmann, Marius (2010). The physics of semiconductors : an introduction including nanophysics and applications (2nd ed.). Springer. p. 87. ISBN 978-3-642-13883-6.
- Soboyejo, Wole (2003). "7.3 Dislocation Velocity". Mechanical properties of engineered materials. Marcel Dekker. ISBN 0-8247-8900-8. OCLC 300921090.
- ^ Reed-Hill, R.E.; Abbaschian, Reza (1994). Physical Metallurgy Principles. Boston: PWS Publishing Company. ISBN 0-534-92173-6.
- James Shackelford (2009). Introduction to Materials Science for Engineers (7th ed.). Upper Saddle River, NJ: Pearson Prentice Hall. pp. 110–11. ISBN 978-0-13-601260-3.
- James Shackelford (2009). Introduction to Materials Science for Engineers (7th ed.). Upper Saddle River, NJ: Pearson Prentice Hall. pp. 110–11. ISBN 978-0-13-601260-3.
- ^ Föll, Helmut. "Defects in Crystals". Retrieved 2019-11-09.
- "Reaction Forming a Stair-Rod Dislocation". Retrieved 26 Nov 2019.
- Cai, W.; Nix, W. D. (2016). Imperfections in crystalline solids. Cambridge, UK: Cambridge University Press.
- ^ Courtney, T. H. (2000). Mechanical behavior of materials. Long Grove, IL: Waveland.
- Gasser, U.; Eisenmann, C.; Maret, G.; Keim, P. (2010). "Melting of crystals in two dimensions". ChemPhysChem. 11 (5): 963–970. doi:10.1002/cphc.200900755. PMID 20099292.
- Spence, J.C.H.; et al. (2006). "Imaging dislocation cores – the way forward". Philosophical Magazine. 86 (29–31): 4781–4796. Bibcode:2006PMag...86.4781S. doi:10.1080/14786430600776322. S2CID 135976739.
- Williams, David B.; Carter, C. Barry (2008). Transmission electron microscopy : a textbook for materials science. Springer. ISBN 9780387765020. OCLC 660999227.
- Peach, M.; Koehler, J. S. (1950-11-01). "The Forces Exerted on Dislocations and the Stress Fields Produced by Them". Physical Review. 80 (3): 436–439. Bibcode:1950PhRv...80..436P. doi:10.1103/PhysRev.80.436.
- Suzuki, Taira (1991). Dislocation Dynamics and Plasticity. Takeuchi, Shin., Yoshinaga, Hideo. Berlin, Heidelberg: Springer Berlin Heidelberg. p. 8. ISBN 978-3-642-75774-7. OCLC 851741787.
- Soboyejo, Winston O. (2003). "6 Introduction to Dislocation Mechanics". Mechanical properties of engineered materials. New York: Marcel Dekker. ISBN 0-8247-8900-8. OCLC 50868191.
External links
- Defects in Crystals/ Prof. Dr. Helmut Föll website Chapter 5 contains a wealth of information on dislocations;
- DoITPoMS Online tutorial on dislocations, including movies of dislocations in bubble rafts;
- Difference between Edge dislocation and Screw dislocation Difference between Edge dislocation and Screw dislocation in detail;
- Scanning Tunneling Microscope – Gallery Image gallery, including a dislocations page, seen at the atomic level of metal surfaces, by the surface physics group at the Faculty of Physics, Vienna University of Technology, Austria.
- Volterra, V., "On the equilibrium of multiply-connected bodies," trans. by D. H. Delphenich
- Somigliana, C., "On the theory of elastic distortions," transl. by D. H. Delphenich
| Crystallography | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Key concepts |
|  | ||||||||||
| Characterisation | ||||||||||||
| Algorithms | ||||||||||||
| Software | ||||||||||||
| Databases | ||||||||||||
| Journals | ||||||||||||
| Awards | ||||||||||||
| Organisation |
| |||||||||||
 , shear strength
, shear strength  is given approximately by:
is given approximately by:

 i.e., typically less than
i.e., typically less than  ) the dislocation density increases due to the formation of new dislocations. The consequent increasing overlap between the strain fields of adjacent dislocations gradually increases the resistance to further dislocation motion. This causes a hardening of the metal as deformation progresses. This effect is known as
) the dislocation density increases due to the formation of new dislocations. The consequent increasing overlap between the strain fields of adjacent dislocations gradually increases the resistance to further dislocation motion. This causes a hardening of the metal as deformation progresses. This effect is known as  in a material can be increased by plastic deformation by the following relationship:
in a material can be increased by plastic deformation by the following relationship:
 .
. , where
, where  , we see that the required stress is 3.4 GPa, which is very close to the theoretical strength of the crystal. Therefore, in conventional deformation homogeneous nucleation requires a concentrated stress, and is very unlikely. Grain boundary initiation and interface interaction are more common sources of dislocations.
, we see that the required stress is 3.4 GPa, which is very close to the theoretical strength of the crystal. Therefore, in conventional deformation homogeneous nucleation requires a concentrated stress, and is very unlikely. Grain boundary initiation and interface interaction are more common sources of dislocations.

 is a material constant,
is a material constant,  is the applied shear stress,
is the applied shear stress,  is a constant that decreases with increasing temperature. Increased shear stress will increase the dislocation velocity, while increased temperature will typically decrease the dislocation velocity. Greater phonon scattering at higher temperatures is hypothesized to be responsible for increased damping forces which slow the dislocation movement.
is a constant that decreases with increasing temperature. Increased shear stress will increase the dislocation velocity, while increased temperature will typically decrease the dislocation velocity. Greater phonon scattering at higher temperatures is hypothesized to be responsible for increased damping forces which slow the dislocation movement.



 is the
is the  is the
is the  is
is  and
and  are coordinates.
are coordinates.

 is a radial coordinate.
This equation suggests a long cylinder of stress radiating outward from the cylinder and decreasing with distance. This simple model results in an infinite value for the core of the dislocation at
is a radial coordinate.
This equation suggests a long cylinder of stress radiating outward from the cylinder and decreasing with distance. This simple model results in an infinite value for the core of the dislocation at  and so it is only valid for stresses outside of the core of the dislocation. If the Burgers vector is very large, the core may actually be empty resulting in a
and so it is only valid for stresses outside of the core of the dislocation. If the Burgers vector is very large, the core may actually be empty resulting in a  , the angle between the line direction and Burgers vector, where
, the angle between the line direction and Burgers vector, where  for pure edge dislocations and
for pure edge dislocations and  for screw dislocations.
for screw dislocations.
 ("g dot b") analysis. When performing
("g dot b") analysis. When performing  vector. The contrast of a dislocation is scaled by a factor of the
vector. The contrast of a dislocation is scaled by a factor of the  , and the sense vector,
, and the sense vector,  .
.

 , and the sense vector,
, and the sense vector, 

 . The work done by displacing cut faces parallel to a chosen axis that creates one dislocation in the stress field of another displacement. For the
. The work done by displacing cut faces parallel to a chosen axis that creates one dislocation in the stress field of another displacement. For the 


 is the distance from free surface in the
is the distance from free surface in the  can be expressed as:
can be expressed as:
