Misplaced Pages

Crypto-PAn

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Cryptographic algorithm for anonymizing IP addresses
This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (September 2018)

Crypto-PAn (Cryptography-based Prefix-preserving Anonymization) is a cryptographic algorithm for anonymizing IP addresses while preserving their subnet structure. That is, the algorithm encrypts any string of bits x {\displaystyle x} to a new string E k ( x ) {\displaystyle E_{k}(x)} , while ensuring that for any pair of bit-strings x , y {\displaystyle x,y} which share a common prefix of length p {\displaystyle p} , their images E k ( x ) , E k ( y ) {\displaystyle E_{k}(x),E_{k}(y)} also share a common prefix of length p {\displaystyle p} . A mapping with this property is called prefix-preserving. In this way, Crypto-PAn is a kind of format-preserving encryption.

The mathematical outline of Crypto-PAn was developed by Jinliang Fan, Jun Xu, Mostafa H. Ammar (all of Georgia Tech) and Sue B. Moon. It was inspired by the IP address anonymization done by Greg Minshall's TCPdpriv program circa 1996.

Algorithm

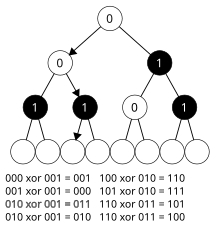
A diagram of the Crypto-PAn algorithm as a tree descent. The nodes of the tree are colored according to a pseudo-random function of the key material (not shown). The arrows show the descent corresponding to the input bit-string "010". That descent's nodes are colored "001"; the anonymized output string is thus "011".

Intuitively, Crypto-PAn encrypts a bit-string of length n {\displaystyle n} by descending a binary tree of depth n {\displaystyle n} , one step for each bit in the string. Each of the binary tree's 2 n − 1 {\displaystyle 2^{n}-1} non-leaf nodes has been given a value of "0" or "1", according to some pseudo-random function seeded by the encryption key. At each step i {\displaystyle i} of the descent, the algorithm computes the i {\displaystyle i} th bit of the output by XORing the i {\displaystyle i} th bit of the input with the value of the current node.

The reference implementation takes a 256-bit key. The first 128 bits of the key material are used to initialize an AES-128 cipher in ECB mode. The second 128 bits of the key material are encrypted with the cipher to produce a 128-bit padding block p a d {\displaystyle {\mathit {pad}}} .

Given a 32-bit IPv4 address x {\displaystyle x} , the reference implementation performs the following operation for each bit x i {\displaystyle x_{i}} of the input: Compose a 128-bit input block I i = x [ 0 , i ) p a d [ i , 128 ) {\displaystyle I_{i}=x_{[0,i)}{\mathit {pad}}_{[i,128)}} . Encrypt I i {\displaystyle I_{i}} with the cipher to produce a 128-bit output block O i {\displaystyle O_{i}} . Finally, XOR the i {\displaystyle i} th bit of that output block with the i {\displaystyle i} th bit of x {\displaystyle x} , and append the result — x i ⊕ O i , i {\displaystyle x_{i}\oplus O_{i,i}} — onto the output bitstring. Once all 32 bits of the output bitstring have been computed, the result is returned as the anonymized output E k ( x ) {\displaystyle E_{k}(x)} which corresponds to the original input x {\displaystyle x} .

The reference implementation does not implement deanonymization; that is, it does not provide a function D k {\displaystyle D_{k}} such that D k ( E k ( x ) ) = x {\displaystyle D_{k}(E_{k}(x))=x} . However, decryption can be implemented almost identically to encryption, just making sure to compose each input block I i = x [ 0 , i ) p a d [ i , 128 ) {\displaystyle I_{i}=x_{[0,i)}{\mathit {pad}}_{[i,128)}} using the plaintext bits of x {\displaystyle x} decrypted so far, rather than using the ciphertext bits: I i ≠ E k ( x ) [ 0 , i ) p a d [ i , 128 ) {\displaystyle I_{i}\neq E_{k}(x)_{[0,i)}{\mathit {pad}}_{[i,128)}} .

The reference implementation does not implement encryption of bitstrings of lengths other than 32; for example, it does not support the anonymization of 128-bit IPv6 addresses. In practice, the 32-bit Crypto-PAn algorithm can be used in "ECB mode" itself, so that a 128-bit string x [ 0 , 128 ) {\displaystyle x_{[0,128)}} might be anonymized as E k ( x [ 0 , 32 ) ) E k ( x [ 32 , 64 ) ) E k ( x [ 64 , 96 ) ) E k ( x [ 96 , 128 ) ) {\displaystyle E_{k}(x_{[0,32)})E_{k}(x_{[32,64)})E_{k}(x_{[64,96)})E_{k}(x_{[96,128)})} . This approach preserves the prefix structure of the 128-bit string, but does leak information about the lower-order chunks; for example, an anonymized IPv6 address consisting of the same 32-bit ciphertext repeated four times is likely the special address ::, which thus reveals the encryption of the 32-bit plaintext 0000:0000:0000:0000.

In principle, the reference implementation's approach (building 128-bit input blocks I i {\displaystyle I_{i}} ) can be extended up to 128 bits. Beyond 128 bits, a different approach would have to be used; but the fundamental algorithm (descending a binary tree whose nodes are marked with a pseudo-random function of the key material) remains valid.

Implementations

Crypto-PAn's C++ reference implementation was written in 2002 by Jinliang Fan.

In 2005, David Stott of Lucent made some improvements to the C++ reference implementation, including a deanonymization routine. Stott also observed that the algorithm preserves prefix structure while destroying suffix structure; running the Crypto-PAn algorithm on a bit-reversed string will preserve any existing suffix structure while destroying prefix structure. Thus, running the algorithm first on the input string, and then again on the bit-reversed output of the first pass, destroys both prefix and suffix structure. (However, once the suffix structure has been destroyed, destroying the remaining prefix structure can be accomplished far more efficiently by simply feeding the non-reversed output to AES-128 in ECB mode. There is no particular reason to reuse Crypto-PAn in the second pass.)

A Perl implementation was written in 2005 by John Kristoff. Python and Ruby implementations also exist.

Versions of the Crypto-PAn algorithm are used for data anonymization in many applications, including NetSniff and CAIDA's CoralReef library.

References

  1. ^ Jinliang Fan (April 2002). "Crypto-PAn.1.0.tar.gz (reference implementation)". Archived from the original on 2018-09-08. Retrieved 2018-09-07.
  2. Jun Xu; Jinliang Fan; Mostafa H. Ammar; Sue B. Moon (2001). "On the Design and Performance of Prefix-Preserving IP Traffic Trace Anonymization" (PDF). Proceedings of the First ACM SIGCOMM Workshop on Internet Measurement. Archived (PDF) from the original on 2018-09-08. Retrieved 2018-09-07.
  3. ^ Jun Xu; Jinliang Fan; Mostafa H. Ammar; Sue B. Moon (2002). "Prefix-preserving IP address anonymization: Measurement-based security evaluation and a new cryptography-based scheme". Computer Networks. 46 (2): 253–272. doi:10.1016/j.comnet.2004.03.033. hdl:1853/6549. ISBN 0769518567. S2CID 6518311.
  4. ^ David Stott (August 2005). "Lucent's Extensions to Cryptopan". Archived from the original on 2018-09-08. Retrieved 2018-09-07.
  5. John Kristoff (November 2005). "IP-Anonymous 0.04". Archived from the original on 2018-09-08. Retrieved 2018-09-07.
  6. Michael Bauer (2013-08-26). "pycryptopan 0.01d". Python Package Index. Archived from the original on 2018-09-08. Retrieved 2018-09-07.
  7. Peter Wood (2016-09-25). "CryptoPAn 0.1.0". rubygems.org. Archived from the original on 2018-09-08. Retrieved 2018-09-07.
  8. "NetSniff / IP Address Anonymisation Modes / Crypto-PAn". 2007-06-26. Archived from the original on 2018-04-11. Retrieved 2018-09-07.
  9. "Documentation for the C Coral API / IP address anonymization". 29 March 2000. Archived from the original on 2016-12-02. Retrieved 2018-09-07.
Categories:
Crypto-PAn Add topic