Isaac Newton's rotating bucket argument (also known as Newton's bucket) is a thought experiment that was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five arguments from the "properties, causes, and effects" of "true motion and rest" that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime.
Background
These arguments, and a discussion of the distinctions between absolute and relative time, space, place and motion, appear in a scholium at the end of Definitions sections in Book I of Newton's work, The Mathematical Principles of Natural Philosophy (1687) (not to be confused with General Scholium at the end of Book III), which established the foundations of classical mechanics and introduced his law of universal gravitation, which yielded the first quantitatively adequate dynamical explanation of planetary motion.
Despite their embrace of the principle of rectilinear inertia and the recognition of the kinematical relativity of apparent motion (which underlies whether the Ptolemaic or the Copernican system is correct), natural philosophers of the seventeenth century continued to consider true motion and rest as physically separate descriptors of an individual body. The dominant view Newton opposed was devised by René Descartes, and was supported (in part) by Gottfried Leibniz. It held that empty space is a metaphysical impossibility because space is nothing other than the extension of matter, or, in other words, that when one speaks of the space between things one is actually making reference to the relationship that exists between those things and not to some entity that stands between them. Concordant with the above understanding, any assertion about the motion of a body boils down to a description over time in which the body under consideration is at t1 found in the vicinity of one group of "landmark" bodies and at some t2 is found in the vicinity of some other "landmark" body or bodies.
Descartes recognized that there would be a real difference, however, between a situation in which a body with movable parts and originally at rest with respect to a surrounding ring was itself accelerated to a certain angular velocity with respect to the ring, and another situation in which the surrounding ring were given a contrary acceleration with respect to the central object. With sole regard to the central object and the surrounding ring, the motions would be indistinguishable from each other assuming that both the central object and the surrounding ring were absolutely rigid objects. However, if neither the central object nor the surrounding ring were absolutely rigid then the parts of one or both of them would tend to fly out from the axis of rotation.
For contingent reasons having to do with the Inquisition, Descartes spoke of motion as both absolute and relative.
By the late 19th century, the contention that all motion is relative was re-introduced, notably by Ernst Mach (1883).
When, accordingly, we say that a body preserves unchanged its direction and velocity in space, our assertion is nothing more or less than an abbreviated reference to the entire universe.
— Ernst Mach; as quoted by Ciufolini and Wheeler: Gravitation and Inertia, p. 387
The argument
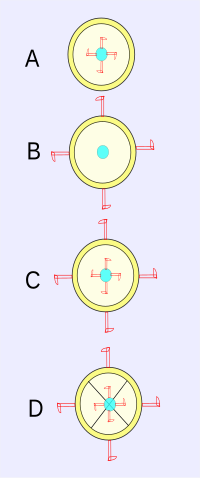
Newton discusses a bucket (Latin: situla) filled with water hung by a cord. If the cord is twisted up tightly on itself and then the bucket is released, it begins to spin rapidly, not only with respect to the experimenter, but also in relation to the water it contains. (This situation would correspond to diagram B above.)
Although the relative motion at this stage is the greatest, the surface of the water remains flat, indicating that the parts of the water have no tendency to recede from the axis of relative motion, despite proximity to the pail. Eventually, as the cord continues to unwind, the surface of the water assumes a concave shape as it acquires the motion of the bucket spinning relative to the experimenter. This concave shape shows that the water is rotating, despite the fact that the water is at rest relative to the pail. In other words, it is not the relative motion of the pail and water that causes concavity of the water, contrary to the idea that motions can only be relative, and that there is no absolute motion. (This situation would correspond to diagram D.) Possibly the concavity of the water shows rotation relative to something else: say absolute space? Newton says: "One can find out and measure the true and absolute circular motion of the water".
In the 1846 Andrew Motte translation of Newton's words:
If a vessel, hung by a long cord, is so often turned about that the cord is strongly twisted, then filled with water, and held at rest together with the water; after, by the sudden action of another force, it is whirled about in the contrary way, and while the cord is untwisting itself, the vessel continues for some time this motion; the surface of the water will at first be plain, as before the vessel began to move; but the vessel by gradually communicating its motion to the water, will make it begin sensibly to revolve, and recede by little and little, and ascend to the sides of the vessel, forming itself into a concave figure... This ascent of the water shows its endeavour to recede from the axis of its motion; and the true and absolute circular motion of the water, which is here directly contrary to the relative, discovers itself, and may be measured by this endeavour. ... And therefore, this endeavour does not depend upon any translation of the water in respect to ambient bodies, nor can true circular motion be defined by such translation. ...; but relative motions...are altogether destitute of any real effect. ... It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motions of particular bodies from the apparent; because the parts of that immovable space in which these motions are performed, do by no means come under the observations of our senses.
— Isaac Newton; Principia, Book 1: Scholium
The argument that the motion is absolute, not relative, is incomplete, as it limits the participants relevant to the experiment to only the pail and the water, a limitation that has not been established. In fact, the concavity of the water clearly involves gravitational attraction, and by implication the Earth also is a participant. Here is a critique due to Mach arguing that only relative motion is established:
Newton's experiment with the rotating vessel of water simply informs us that the relative rotation of the water with respect to the sides of the vessel produces no noticeable centrifugal forces, but that such forces are produced by its relative rotations with respect to the mass of the earth and other celestial bodies.
— Ernst Mach, as quoted by L. Bouquiaux in Leibniz, p. 104
The degree in which Mach's hypothesis is integrated in general relativity is discussed in the article Mach's principle; it is generally held that general relativity is not entirely Machian.
All observers agree that the surface of rotating water is curved. However, the explanation of this curvature involves centrifugal force for all observers with the exception of a truly stationary observer, who finds the curvature is consistent with the rate of rotation of the water as they observe it, with no need for an additional centrifugal force. Thus, a stationary frame can be identified, and it is not necessary to ask "Stationary with respect to what?":
The original question, "relative to what frame of reference do the laws of motion hold?" is revealed to be wrongly posed. For the laws of motion essentially determine a class of reference frames, and (in principle) a procedure for constructing them.
A supplementary thought experiment with the same objective of determining the occurrence of absolute rotation also was proposed by Newton: the example of observing two identical spheres in rotation about their center of gravity and tied together by a string. Occurrence of tension in the string is indicative of absolute rotation; see Rotating spheres.
Detailed analysis

The historic interest of the rotating bucket experiment is its usefulness in suggesting one can detect absolute rotation by observation of the shape of the surface of the water. However, one might question just how rotation brings about this change. Below are two approaches to understanding the concavity of the surface of rotating water in a bucket.

Newton's laws of motion
The shape of the surface of a rotating liquid in a bucket can be determined using Newton's laws for the various forces on an element of the surface. For example, see Knudsen and Hjorth. The analysis begins with the free body diagram in the co-rotating frame where the water appears stationary. The height of the water h = h(r) is a function of the radial distance r from the axis of rotation Ω, and the aim is to determine this function. An element of water volume on the surface is shown to be subject to three forces: the vertical force due to gravity Fg, the horizontal, radially outward centrifugal force FCfgl, and the force normal to the surface of the water Fn due to the rest of the water surrounding the selected element of surface. The force due to surrounding water is known to be normal to the surface of the water because a liquid in equilibrium cannot support shear stresses. To quote Anthony and Brackett:
The surface of a fluid of uniform density..., if at rest, is everywhere perpendicular to the lines of force; for if this were not so, the force at a point on the surface could be resolved into two components, one perpendicular and the other tangent to the surface. But from the nature of a fluid, the tangential force would set up a motion of the fluid, which is contrary to the statement that the fluid is at rest.
— William Arnold Anthony & Cyrus Fogg Brackett: Elementary Text-book of Physics, p. 127
Moreover, because the element of water does not move, the sum of all three forces must be zero. To sum to zero, the force of the water must point oppositely to the sum of the centrifugal and gravity forces, which means the surface of the water must adjust so its normal points in this direction. (A very similar problem is the design of a banked turn, where the slope of the turn is set so a car will not slide off the road. The analogy in the case of rotating bucket is that the element of water surface will "slide" up or down the surface unless the normal to the surface aligns with the vector resultant formed by the vector addition Fg + FCfgl.)
As r increases, the centrifugal force increases according to the relation (the equations are written per unit mass):
where Ω is the constant rate of rotation of the water. The gravitational force is unchanged at
where g is the acceleration due to gravity. These two forces add to make a resultant at an angle φ from the vertical given by
which clearly becomes larger as r increases. To ensure that this resultant is normal to the surface of the water, and therefore can be effectively nulled by the force of the water beneath, the normal to the surface must have the same angle, that is,
leading to the ordinary differential equation for the shape of the surface:
or, integrating:
where h(0) is the height of the water at r = 0. In other words, the surface of the water is parabolic in its dependence upon the radius.
Potential energy
The shape of the water's surface can be found in a different, very intuitive way using the interesting idea of the potential energy associated with the centrifugal force in the co-rotating frame. In a reference frame uniformly rotating at angular rate Ω, the fictitious centrifugal force is conservative and has a potential energy of the form:
where r is the radius from the axis of rotation. This result can be verified by taking the gradient of the potential to obtain the radially outward force:
The meaning of the potential energy (stored work) is that movement of a test body from a larger radius to a smaller radius involves doing work against the centrifugal force and thus gaining potential energy. But this test body at the smaller radius where its elevation is lower has now lost equivalent gravitational potential energy.
Potential energy therefore explains the concavity of the water surface in a rotating bucket. Notice that at equilibrium the surface adopts a shape such that an element of volume at any location on its surface has the same potential energy as at any other. That being so, no element of water on the surface has any incentive to move position, because all positions are equivalent in energy. That is, equilibrium is attained. On the other hand, were surface regions with lower energy available, the water occupying surface locations of higher potential energy would move to occupy these positions of lower energy, inasmuch as there is no barrier to lateral movement in an ideal liquid.
We might imagine deliberately upsetting this equilibrium situation by somehow momentarily altering the surface shape of the water to make it different from an equal-energy surface. This change in shape would not be stable, and the water would not stay in our artificially contrived shape, but engage in a transient exploration of many shapes until non-ideal frictional forces introduced by sloshing, either against the sides of the bucket or by the non-ideal nature of the liquid, killed the oscillations and the water settled down to the equilibrium shape.
To see the principle of an equal-energy surface at work, imagine gradually increasing the rate of rotation of the bucket from zero. The water surface is flat at first, and clearly a surface of equal potential energy because all points on the surface are at the same height in the gravitational field acting upon the water. At some small angular rate of rotation, however, an element of surface water can achieve lower potential energy by moving outward under the influence of the centrifugal force; think of an object moving with the force of gravity closer to the Earth's center: the object lowers its potential energy by complying with a force. Because water is incompressible and must remain within the confines of the bucket, this outward movement increases the depth of water at the larger radius, increasing the height of the surface at larger radius, and lowering it at smaller radius. The surface of the water becomes slightly concave, with the consequence that the potential energy of the water at the greater radius is increased by the work done against gravity to achieve the greater height. As the height of water increases, movement toward the periphery becomes no longer advantageous, because the reduction in potential energy from working with the centrifugal force is balanced against the increase in energy working against gravity. Thus, at a given angular rate of rotation, a concave surface represents the stable situation, and the more rapid the rotation, the more concave this surface. If rotation is arrested, the energy stored in fashioning the concave surface must be dissipated, for example through friction, before an equilibrium flat surface is restored.
To implement a surface of constant potential energy quantitatively, let the height of the water be : then the potential energy per unit mass contributed by gravity is and the total potential energy per unit mass on the surface is
with the background energy level independent of r. In a static situation (no motion of the fluid in the rotating frame), this energy is constant independent of position r. Requiring the energy to be constant, we obtain the parabolic form:
where h(0) is the height at r = 0 (the axis). See Figures 1 and 2.
The principle of operation of the centrifuge also can be simply understood in terms of this expression for the potential energy, which shows that it is favorable energetically when the volume far from the axis of rotation is occupied by the heavier substance.
See also
- Centrifugal force
- Inertial frame of reference
- Mach's principle
- Philosophy of space and time: Absolutism vs. relationalism
- Rotating reference frame
- Rotating spheres
- Rotational gravity
- Sagnac effect
References
- Disalle, Robert (2002). Cohen, I. Bernard; Smith, George E. (eds.). The Cambridge Companion to Newton. Cambridge University Press. p. 43. ISBN 0-521-65696-6.
- Gilson, James G. (September 1, 2004), Mach's Principle II, arXiv:physics/0409010, Bibcode:2004physics...9010G
- See the Principia on line at Andrew Motte translation, pp. 77–82.
- Descartes, René (1988). Descartes: Selected Philosophical Writings. Translated by Cottingham, John. Cambridge University Press. p. 191. ISBN 0-521-35812-4.
- Alexandre Koyre (1957). From the Closed World to the Infinite Universe. Forgotten Books. p. 75. ISBN 1-60620-143-3.
- René Descartes (1664). Principia Philosophiae. Part II, §25.
- Daniel Garber (1992). Descartes' Metaphysical Physics. University of Chicago Press. p. 170. ISBN 0-226-28219-8.
- Robert Disalle (2006). Understanding Space-time: The philosophical development of physics from Newton to Einstein. Cambridge University Press. p. 19. ISBN 0-521-85790-2.
- Mach, E. (1960 ), The Science of Mechanics, LaSalle, IL: Open Court Publishing, p. 284.
- Ignazio Ciufolini, John Archibald Wheeler (1995). Gravitation and Inertia. Princeton University Press. pp. 386–387. ISBN 0-691-03323-4.
- For a discussion of Newton's original argument, see Max Born & Günther Leibfried (January 1962). Einstein's Theory of Relativity. New York: Courier Dover Publications. pp. 78–79. ISBN 0-486-60769-0.
- Robert Disalle (25 April 2002). "Newton's philosophical analysis of space and time". In I. Bernard Cohen, George Edwin Smith (ed.). op. cit.. Cambridge University Press. p. 45. ISBN 0-521-65696-6.
- See the Principia on line at Andrew Motte Translation pp. 79-81
- Bouquiaux, L. (2008). Dascal, Marcelo (ed.). Leibniz. Springer. p. 104. ISBN 978-1-4020-8667-0.
- Robert DiSalle (Summer 2002). "Space and Time: Inertial Frames". In Edward N. Zalta (ed.). The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- Jens M. Knudsen, Poul G. Hjorth (2000). Elements of Newtonian Mechanics (3rd ed.). Springer. p. 143. ISBN 3-540-67652-X.
- Lawrence S. Lerner (1997). Physics for Scientists and Engineers. Jones & Bartlett. p. 404. ISBN 0-86720-479-6.
- William Arnold Anthony & Cyrus Fogg Brackett (1884). Elementary Text-book of Physics. Wiley. p. 127.
pascal's law.
- Robert Daniel Carmichael (1920). The Theory of Relativity. John Wiley & Sons. p. 78.
fictitious Christoffel potential.
- Hans J. Weber & George B. Arfken (2003). Essential mathematical methods for physicists. Academic Press. p. 79. ISBN 0-12-059877-9.
Further reading
- Brian Greene (2004). "Chapter 2, The Universe and the Bucket". The Fabric of the Cosmos: Space, Time, and the Texture of Reality. A A Knopf. ISBN 0-375-41288-3.
- The isotropy of the cosmic microwave background radiation is another indicator that the universe does not rotate. See:
- R. B. Partridge (1995). 3 K: The Cosmic Microwave Background Radiation. Cambridge University Press. pp. 279–280. ISBN 0-521-35254-1.
- D. Lynden-Bell (1996). Relativistic Astrophysics (Igor' Dmitrievich Novikov, Bernard Jean Trefor Jones, Draza Marković (Editors) ed.). Cambridge University Press. p. 167. ISBN 0-521-62113-5.
- Ralph A. Alpher and Robert Herman (1975). Big bang cosmology and the cosmic black-body radiation (in Proc. Am. Philos. Soc. vol. 119, no. 5 (1975) ed.). American Philosophical Society. pp. 325–348. ISBN 9781422371077.
External links
- Newton's Views on Space, Time, and Motion from Stanford Encyclopedia of Philosophy, article by Robert Rynasiewicz. At the end of this article, loss of fine distinctions in the translations as compared to the original Latin text is discussed.
- Life and Philosophy of Leibniz see section on Space, Time and Indiscernibles for Leibniz arguing against the idea of space acting as a causal agent.
- Newton's Bucket An interactive applet illustrating the water shape, and an attached PDF file with a mathematical derivation of a more complete water-shape model than is given in this article.









 : then the potential energy per unit mass contributed by gravity is
: then the potential energy per unit mass contributed by gravity is  and the total potential energy per unit mass on the surface is
and the total potential energy per unit mass on the surface is

 the background energy level independent of r. In a static situation (no motion of the fluid in the rotating frame), this energy is constant independent of position r. Requiring the energy to be constant, we obtain the
the background energy level independent of r. In a static situation (no motion of the fluid in the rotating frame), this energy is constant independent of position r. Requiring the energy to be constant, we obtain the 