
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements), usually arranged along a common axis. Lenses are made from materials such as glass or plastic and are ground, polished, or molded to the required shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called "lenses", such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses.
Lenses are used in various imaging devices such as telescopes, binoculars, and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia.
History
See also: History of optics and Camera lens| This section needs expansion with: history after 1823. You can help by adding to it. (January 2012) |


The word lens comes from lēns, the Latin name of the lentil (a seed of a lentil plant), because a double-convex lens is lentil-shaped. The lentil also gives its name to a geometric figure.
Some scholars argue that the archeological evidence indicates that there was widespread use of lenses in antiquity, spanning several millennia. The so-called Nimrud lens is a rock crystal artifact dated to the 7th century BCE which may or may not have been used as a magnifying glass, or a burning glass. Others have suggested that certain Egyptian hieroglyphs depict "simple glass meniscal lenses".
The oldest certain reference to the use of lenses is from Aristophanes' play The Clouds (424 BCE) mentioning a burning-glass. Pliny the Elder (1st century) confirms that burning-glasses were known in the Roman period. Pliny also has the earliest known reference to the use of a corrective lens when he mentions that Nero was said to watch the gladiatorial games using an emerald (presumably concave to correct for nearsightedness, though the reference is vague). Both Pliny and Seneca the Younger (3 BC–65 AD) described the magnifying effect of a glass globe filled with water.
Ptolemy (2nd century) wrote a book on Optics, which however survives only in the Latin translation of an incomplete and very poor Arabic translation. The book was, however, received by medieval scholars in the Islamic world, and commented upon by Ibn Sahl (10th century), who was in turn improved upon by Alhazen (Book of Optics, 11th century). The Arabic translation of Ptolemy's Optics became available in Latin translation in the 12th century (Eugenius of Palermo 1154). Between the 11th and 13th century "reading stones" were invented. These were primitive plano-convex lenses initially made by cutting a glass sphere in half. The medieval (11th or 12th century) rock crystal Visby lenses may or may not have been intended for use as burning glasses.
Spectacles were invented as an improvement of the "reading stones" of the high medieval period in Northern Italy in the second half of the 13th century. This was the start of the optical industry of grinding and polishing lenses for spectacles, first in Venice and Florence in the late 13th century, and later in the spectacle-making centres in both the Netherlands and Germany. Spectacle makers created improved types of lenses for the correction of vision based more on empirical knowledge gained from observing the effects of the lenses (probably without the knowledge of the rudimentary optical theory of the day). The practical development and experimentation with lenses led to the invention of the compound optical microscope around 1595, and the refracting telescope in 1608, both of which appeared in the spectacle-making centres in the Netherlands.
Further information: History of the telescopeWith the invention of the telescope and microscope there was a great deal of experimentation with lens shapes in the 17th and early 18th centuries by those trying to correct chromatic errors seen in lenses. Opticians tried to construct lenses of varying forms of curvature, wrongly assuming errors arose from defects in the spherical figure of their surfaces. Optical theory on refraction and experimentation was showing no single-element lens could bring all colours to a focus. This led to the invention of the compound achromatic lens by Chester Moore Hall in England in 1733, an invention also claimed by fellow Englishman John Dollond in a 1758 patent.
Developments in transatlantic commerce were the impetus for the construction of modern lighthouses in the 18th century, which utilize a combination of elevated sightlines, lighting sources, and lenses to provide navigational aid overseas. With maximal distance of visibility needed in lighthouses, conventional convex lenses would need to be significantly sized which would negatively affect the development of lighthouses in terms of cost, design, and implementation. Fresnel lens were developed that considered these constraints by featuring less material through their concentric annular sectioning. They were first fully implemented into a lighthouse in 1823.
Construction of simple lenses
Most lenses are spherical lenses: their two surfaces are parts of the surfaces of spheres. Each surface can be convex (bulging outwards from the lens), concave (depressed into the lens), or planar (flat). The line joining the centres of the spheres making up the lens surfaces is called the axis of the lens. Typically the lens axis passes through the physical centre of the lens, because of the way they are manufactured. Lenses may be cut or ground after manufacturing to give them a different shape or size. The lens axis may then not pass through the physical centre of the lens.
Toric or sphero-cylindrical lenses have surfaces with two different radii of curvature in two orthogonal planes. They have a different focal power in different meridians. This forms an astigmatic lens. An example is eyeglass lenses that are used to correct astigmatism in someone's eye.
Types of simple lenses
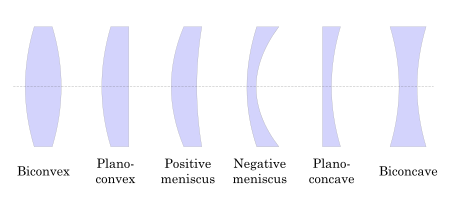
Lenses are classified by the curvature of the two optical surfaces. A lens is biconvex (or double convex, or just convex) if both surfaces are convex. If both surfaces have the same radius of curvature, the lens is equiconvex. A lens with two concave surfaces is biconcave (or just concave). If one of the surfaces is flat, the lens is plano-convex or plano-concave depending on the curvature of the other surface. A lens with one convex and one concave side is convex-concave or meniscus. Convex-concave lenses are most commonly used in corrective lenses, since the shape minimizes some aberrations.
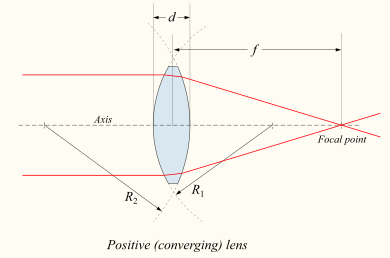
For a biconvex or plano-convex lens in a lower-index medium, a collimated beam of light passing through the lens converges to a spot (a focus) behind the lens. In this case, the lens is called a positive or converging lens. For a thin lens in air, the distance from the lens to the spot is the focal length of the lens, which is commonly represented by f in diagrams and equations. An extended hemispherical lens is a special type of plano-convex lens, in which the lens's curved surface is a full hemisphere and the lens is much thicker than the radius of curvature.
Another extreme case of a thick convex lens is a ball lens, whose shape is completely round. When used in novelty photography it is often called a "lensball". A ball-shaped lens has the advantage of being omnidirectional, but for most optical glass types, its focal point lies close to the ball's surface. Because of the ball's curvature extremes compared to the lens size, optical aberration is much worse than thin lenses, with the notable exception of chromatic aberration.
 |
 |
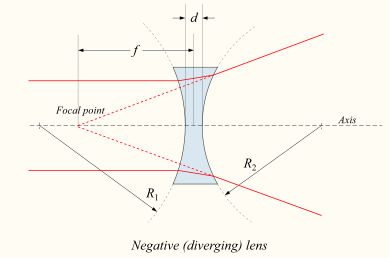
For a biconcave or plano-concave lens in a lower-index medium, a collimated beam of light passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. The beam, after passing through the lens, appears to emanate from a particular point on the axis in front of the lens. For a thin lens in air, the distance from this point to the lens is the focal length, though it is negative with respect to the focal length of a converging lens.
 |
 |
The behavior reverses when a lens is placed in a medium with higher refractive index than the material of the lens. In this case a biconvex or plano-convex lens diverges light, and a biconcave or plano-concave one converges it.

Convex-concave (meniscus) lenses can be either positive or negative, depending on the relative curvatures of the two surfaces. A negative meniscus lens has a steeper concave surface (with a shorter radius than the convex surface) and is thinner at the centre than at the periphery. Conversely, a positive meniscus lens has a steeper convex surface (with a shorter radius than the concave surface) and is thicker at the centre than at the periphery.
An ideal thin lens with two surfaces of equal curvature (also equal in the sign) would have zero optical power (as its focal length becomes infinity as shown in the lensmaker's equation), meaning that it would neither converge nor diverge light. All real lenses have a nonzero thickness, however, which makes a real lens with identical curved surfaces slightly positive. To obtain exactly zero optical power, a meniscus lens must have slightly unequal curvatures to account for the effect of the lens' thickness.
For a spherical surface

For a single refraction for a circular boundary, the relation between object and its image in the paraxial approximation is given by
where R is the radius of the spherical surface, n2 is the refractive index of the material of the surface, n1 is the refractive index of medium (the medium other than the spherical surface material), is the on-axis (on the optical axis) object distance from the line perpendicular to the axis toward the refraction point on the surface (which height is h), and is the on-axis image distance from the line. Due to paraxial approximation where the line of h is close to the vertex of the spherical surface meeting the optical axis on the left, and are also considered distances with respect to the vertex.
Moving toward the right infinity leads to the first or object focal length for the spherical surface. Similarly, toward the left infinity leads to the second or image focal length .
Applying this equation on the two spherical surfaces of a lens and approximating the lens thickness to zero (so a thin lens) leads to the lensmaker's formula.
Derivation

Applying Snell's law on the spherical surface,
Also in the diagram,, and using small angle approximation (paraxial approximation) and eliminating i, r, and θ,
Lensmaker's equation

The (effective) focal length of a spherical lens in air or vacuum for paraxial rays can be calculated from the lensmaker's equation:
where
- is the refractive index of the lens material;
- is the (signed, see below) radius of curvature of the lens surface closer to the light source;
- is the radius of curvature of the lens surface farther from the light source; and
- is the thickness of the lens (the distance along the lens axis between the two surface vertices).
The focal length is with respect to the principal planes of the lens, and the locations of the principal planes and with respect to the respective lens vertices are given by the following formulas, where it is a positive value if it is right to the respective vertex.
The focal length is positive for converging lenses, and negative for diverging lenses. The reciprocal of the focal length, is the optical power of the lens. If the focal length is in metres, this gives the optical power in dioptres (reciprocal metres).
Lenses have the same focal length when light travels from the back to the front as when light goes from the front to the back. Other properties of the lens, such as the aberrations are not the same in both directions.
Sign convention for radii of curvature R1 and R2
Main article: Radius of curvature (optics)The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The sign convention used to represent this varies, but in this article a positive R indicates a surface's center of curvature is further along in the direction of the ray travel (right, in the accompanying diagrams), while negative R means that rays reaching the surface have already passed the center of curvature. Consequently, for external lens surfaces as diagrammed above, R1 > 0 and R2 < 0 indicate convex surfaces (used to converge light in a positive lens), while R1 < 0 and R2 > 0 indicate concave surfaces. The reciprocal of the radius of curvature is called the curvature. A flat surface has zero curvature, and its radius of curvature is infinite.
Sign convention for other parameters
| Parameter | Meaning | + Sign | − Sign |
|---|---|---|---|
| so | The distance between an object and a lens. | Real object | Virtual object |
| si | The distance between an image and a lens. | Real image | Virtual image |
| f | The focal length of a lens. | Conversing lens | Diverging lens |
| yo | The height of an object from the optical axis. | Erect object | Inverted object |
| yi | The height of an image from the optical axis | Erect image | Inverted image |
| MT | The transverse magnification in imaging ( = the ratio of yi to yo ). | Erect image | Inverted image |
This convention seems to be mainly used for this article, although there is another convention such as Cartesian sign convention requiring different lens equation forms.
Thin lens approximation
If d is small compared to R1 and R2 then the thin lens approximation can be made. For a lens in air, f is then given by
Derivation

The spherical thin lens equation in paraxial approximation is derived here with respect to the right figure. The 1st spherical lens surface (which meets the optical axis at as its vertex) images an on-axis object point O to the virtual image I, which can be described by the following equation, For the imaging by second lens surface, by taking the above sign convention, and Adding these two equations yields For the thin lens approximation where the 2nd term of the RHS (Right Hand Side) is gone, so
The focal length of the thin lens is found by limiting
So, the Gaussian thin lens equation is
For the thin lens in air or vacuum where can be assumed, becomes
where the subscript of 2 in is dropped.
Imaging properties
As mentioned above, a positive or converging lens in air focuses a collimated beam travelling along the lens axis to a spot (known as the focal point) at a distance f from the lens. Conversely, a point source of light placed at the focal point is converted into a collimated beam by the lens. These two cases are examples of image formation in lenses. In the former case, an object at an infinite distance (as represented by a collimated beam of waves) is focused to an image at the focal point of the lens. In the latter, an object at the focal length distance from the lens is imaged at infinity. The plane perpendicular to the lens axis situated at a distance f from the lens is called the focal plane.
Lens equation
For paraxial rays, if the distances from an object to a spherical thin lens (a lens of negligible thickness) and from the lens to the image are S1 and S2 respectively, the distances are related by the (Gaussian) thin lens formula:

The right figure shows how the image of an object point can be found by using three rays; the first ray parallelly incident on the lens and refracted toward the second focal point of it, the second ray crossing the optical center of the lens (so its direction does not change), and the third ray toward the first focal point and refracted to the direction parallel to the optical axis. This is a simple ray tracing method easily used. Two rays among the three are sufficient to locate the image point. By moving the object along the optical axis, it is shown that the second ray determines the image size while other rays help to locate the image location.
The lens equation can also be put into the "Newtonian" form:
where and is positive if it is left to the front focal point , and is positive if it is right to the rear focal point . Because is positive, an object point and the corresponding imaging point made by a lens are always in opposite sides with respect to their respective focal points. ( and are either positive or negative.)
This Newtonian form of the lens equation can be derived by using a similarity between triangles P1PO1F1 and L3L2F1 and another similarity between triangles L1L2F2 and P2P02F2 in the right figure. The similarities give the following equations and combining these results gives the Newtonian form of the lens equation.


The above equations also hold for thick lenses (including a compound lens made by multiple lenses, that can be treated as a thick lens) in air or vacuum (which refractive index can be treated as 1) if , , and are with respect to the principal planes of the lens ( is the effective focal length in this case). This is because of triangle similarities like the thin lens case above; similarity between triangles P1PO1F1 and L3H1F1 and another similarity between triangles L1'H2F2 and P2P02F2 in the right figure. If distances S1 or S2 pass through a medium other than air or vacuum, then a more complicated analysis is required.
If an object is placed at a distance S1 > f from a positive lens of focal length f, we will find an image at a distance S2 according to this formula. If a screen is placed at a distance S2 on the opposite side of the lens, an image is formed on it. This sort of image, which can be projected onto a screen or image sensor, is known as a real image. This is the principle of the camera, and also of the human eye, in which the retina serves as the image sensor.
The focusing adjustment of a camera adjusts S2, as using an image distance different from that required by this formula produces a defocused (fuzzy) image for an object at a distance of S1 from the camera. Put another way, modifying S2 causes objects at a different S1 to come into perfect focus.

In some cases, S2 is negative, indicating that the image is formed on the opposite side of the lens from where those rays are being considered. Since the diverging light rays emanating from the lens never come into focus, and those rays are not physically present at the point where they appear to form an image, this is called a virtual image. Unlike real images, a virtual image cannot be projected on a screen, but appears to an observer looking through the lens as if it were a real object at the location of that virtual image. Likewise, it appears to a subsequent lens as if it were an object at that location, so that second lens could again focus that light into a real image, S1 then being measured from the virtual image location behind the first lens to the second lens. This is exactly what the eye does when looking through a magnifying glass. The magnifying glass creates a (magnified) virtual image behind the magnifying glass, but those rays are then re-imaged by the lens of the eye to create a real image on the retina.
 A negative lens produces a demagnified virtual image.
A negative lens produces a demagnified virtual image. A Barlow lens (B) reimages a virtual object (focus of red ray path) into a magnified real image (green rays at focus)
A Barlow lens (B) reimages a virtual object (focus of red ray path) into a magnified real image (green rays at focus)
Using a positive lens of focal length f, a virtual image results when S1 < f, the lens thus being used as a magnifying glass (rather than if S1 ≫ f as for a camera). Using a negative lens (f < 0) with a real object (S1 > 0) can only produce a virtual image (S2 < 0), according to the above formula. It is also possible for the object distance S1 to be negative, in which case the lens sees a so-called virtual object. This happens when the lens is inserted into a converging beam (being focused by a previous lens) before the location of its real image. In that case even a negative lens can project a real image, as is done by a Barlow lens.
For a given lens with the focal length f, the minimum distance between an object and the real image is 4f (S1 = S2 = 2f). This is derived by letting L = S1 + S2, expressing S2 in terms of S1 by the lens equation (or expressing S1 in terms of S2), and equating the derivative of L with respect to S1 (or S2) to zero. (Note that L has no limit in increasing so its extremum is only the minimum, at which the derivate of L is zero.)
 Real image of a lamp is projected onto a screen (inverted). Reflections of the lamp from both surfaces of the biconvex lens are visible.
Real image of a lamp is projected onto a screen (inverted). Reflections of the lamp from both surfaces of the biconvex lens are visible. A convex lens (f ≪ S1) forming a real, inverted image (as the image formed by the objective lens of a telescope or binoculars) rather than the upright, virtual image as seen in a magnifying glass (f > S1). This real image may also be viewed when put on a screen.
A convex lens (f ≪ S1) forming a real, inverted image (as the image formed by the objective lens of a telescope or binoculars) rather than the upright, virtual image as seen in a magnifying glass (f > S1). This real image may also be viewed when put on a screen.
Magnification
The linear magnification of an imaging system using a single lens is given by
where M is the magnification factor defined as the ratio of the size of an image compared to the size of the object. The sign convention here dictates that if M is negative, as it is for real images, the image is upside-down with respect to the object. For virtual images M is positive, so the image is upright.
This magnification formula provides two easy ways to distinguish converging (f > 0) and diverging (f < 0) lenses: For an object very close to the lens (0 < S1 < |f|), a converging lens would form a magnified (bigger) virtual image, whereas a diverging lens would form a demagnified (smaller) image; For an object very far from the lens (S1 > |f| > 0), a converging lens would form an inverted image, whereas a diverging lens would form an upright image.
Linear magnification M is not always the most useful measure of magnifying power. For instance, when characterizing a visual telescope or binoculars that produce only a virtual image, one would be more concerned with the angular magnification—which expresses how much larger a distant object appears through the telescope compared to the naked eye. In the case of a camera one would quote the plate scale, which compares the apparent (angular) size of a distant object to the size of the real image produced at the focus. The plate scale is the reciprocal of the focal length of the camera lens; lenses are categorized as long-focus lenses or wide-angle lenses according to their focal lengths.
Using an inappropriate measurement of magnification can be formally correct but yield a meaningless number. For instance, using a magnifying glass of 5 cm focal length, held 20 cm from the eye and 5 cm from the object, produces a virtual image at infinity of infinite linear size: M = ∞. But the angular magnification is 5, meaning that the object appears 5 times larger to the eye than without the lens. When taking a picture of the moon using a camera with a 50 mm lens, one is not concerned with the linear magnification M ≈ −50 mm / 380000 km = −1.3×10. Rather, the plate scale of the camera is about 1°/mm, from which one can conclude that the 0.5 mm image on the film corresponds to an angular size of the moon seen from earth of about 0.5°.
In the extreme case where an object is an infinite distance away, S1 = ∞, S2 = f and M = −f/∞ = 0, indicating that the object would be imaged to a single point in the focal plane. In fact, the diameter of the projected spot is not actually zero, since diffraction places a lower limit on the size of the point spread function. This is called the diffraction limit.

Table for thin lens imaging properties
| Lens Type | Object Location | Image Type | Image Location | Lateral Image Orientation | Image Magnification | Remark |
|---|---|---|---|---|---|---|
| Converging lens (or positive lens) | Real (rays converging to each image point) | Inverted (opposite to the object orientation) | Diminished | |||
| Converging lens | Real | Inverted | Same size | |||
| Converging lens | Real | Inverted | Magnified | |||
| Converging lens | ||||||
| Converging lens | Virtual (rays apparently diverging from each image point) | Erect (same to the object orientation) | Magnified | As an object moves to the lens, the virtual image also gets closer to the lens while the image size is reduced. | ||
| Diverging lens (or negative lens) | Anywhere | Virtual | Erect | Diminished |
Aberrations
| Optical aberration |
|---|
Lenses do not form perfect images, and always introduce some degree of distortion or aberration that makes the image an imperfect replica of the object. Careful design of the lens system for a particular application minimizes the aberration. Several types of aberration affect image quality, including spherical aberration, coma, and chromatic aberration.
Spherical aberration
Main article: Spherical aberrationSpherical aberration occurs because spherical surfaces are not the ideal shape for a lens, but are by far the simplest shape to which glass can be ground and polished, and so are often used. Spherical aberration causes beams parallel to, but laterally distant from, the lens axis to be focused in a slightly different place than beams close to the axis. This manifests itself as a blurring of the image. Spherical aberration can be minimised with normal lens shapes by carefully choosing the surface curvatures for a particular application. For instance, a plano-convex lens, which is used to focus a collimated beam, produces a sharper focal spot when used with the convex side towards the beam source.
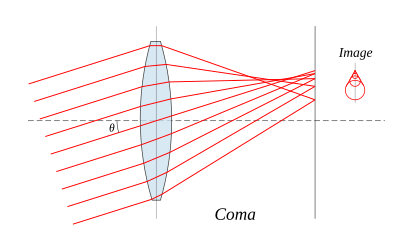
Coma
Main article: Coma (optics)Coma, or comatic aberration, derives its name from the comet-like appearance of the aberrated image. Coma occurs when an object off the optical axis of the lens is imaged, where rays pass through the lens at an angle to the axis θ. Rays that pass through the centre of a lens of focal length f are focused at a point with distance f tan θ from the axis. Rays passing through the outer margins of the lens are focused at different points, either further from the axis (positive coma) or closer to the axis (negative coma). In general, a bundle of parallel rays passing through the lens at a fixed distance from the centre of the lens are focused to a ring-shaped image in the focal plane, known as a comatic circle (see each circle of the image in the below figure). The sum of all these circles results in a V-shaped or comet-like flare. As with spherical aberration, coma can be minimised (and in some cases eliminated) by choosing the curvature of the two lens surfaces to match the application. Lenses in which both spherical aberration and coma are minimised are called bestform lenses.
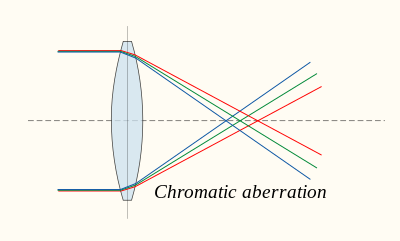
Chromatic aberration
Main article: Chromatic aberrationChromatic aberration is caused by the dispersion of the lens material—the variation of its refractive index, n, with the wavelength of light. Since, from the formulae above, f is dependent upon n, it follows that light of different wavelengths is focused to different positions. Chromatic aberration of a lens is seen as fringes of colour around the image. It can be minimised by using an achromatic doublet (or achromat) in which two materials with differing dispersion are bonded together to form a single lens. This reduces the amount of chromatic aberration over a certain range of wavelengths, though it does not produce perfect correction. The use of achromats was an important step in the development of the optical microscope. An apochromat is a lens or lens system with even better chromatic aberration correction, combined with improved spherical aberration correction. Apochromats are much more expensive than achromats.
Different lens materials may also be used to minimise chromatic aberration, such as specialised coatings or lenses made from the crystal fluorite. This naturally occurring substance has the highest known Abbe number, indicating that the material has low dispersion.
Other types of aberration
Other kinds of aberration include field curvature, barrel and pincushion distortion, and astigmatism.
Aperture diffraction
Even if a lens is designed to minimize or eliminate the aberrations described above, the image quality is still limited by the diffraction of light passing through the lens' finite aperture. A diffraction-limited lens is one in which aberrations have been reduced to the point where the image quality is primarily limited by diffraction under the design conditions.
Compound lenses
See also: Photographic lens, Doublet (lens), Triplet lens, and Achromatic lensSimple lenses are subject to the optical aberrations discussed above. In many cases these aberrations can be compensated for to a great extent by using a combination of simple lenses with complementary aberrations. A compound lens is a collection of simple lenses of different shapes and made of materials of different refractive indices, arranged one after the other with a common axis.
In a multiple-lens system, if the purpose of the system is to image an object, then the system design can be such that each lens treats the image made by the previous lens as an object, and produces the new image of it, so the imaging is cascaded through the lenses. As shown above, the Gaussian lens equation for a spherical lens is derived such that the 2nd surface of the lens images the image made by the 1st lens surface. For multi-lens imaging, 3rd lens surface (the front surface of the 2nd lens) can image the image made by the 2nd surface, and 4th surface (the back surface of the 2nd lens) can also image the image made by the 3rd surface. This imaging cascade by each lens surface justifies the imaging cascade by each lens.
For a two-lens system the object distances of each lens can be denoted as and , and the image distances as and and . If the lenses are thin, each satisfies the thin lens formula
If the distance between the two lenses is , then . (The 2nd lens images the image of the first lens.)
FFD (Front Focal Distance) is defined as the distance between the front (left) focal point of an optical system and its nearest optical surface vertex. If an object is located at the front focal point of the system, then its image made by the system is located infinitely far way to the right (i.e., light rays from the object is collimated after the system). To do this, the image of the 1st lens is located at the focal point of the 2nd lens, i.e., . So, the thin lens formula for the 1st lens becomes
BFD (Back Focal Distance) is similarly defined as the distance between the back (right) focal point of an optical system and its nearest optical surface vertex. If an object is located infinitely far away from the system (to the left), then its image made by the system is located at the back focal point. In this case, the 1st lens images the object at its focal point. So, the thin lens formula for the 2nd lens becomes
A simplest case is where thin lenses are placed in contact (). Then the combined focal length f of the lenses is given by
Since 1/f is the power of a lens with focal length f, it can be seen that the powers of thin lenses in contact are additive. The general case of multiple thin lenses in contact is
where is the number of lenses.
If two thin lenses are separated in air by some distance d, then the focal length for the combined system is given by
As d tends to zero, the focal length of the system tends to the value of f given for thin lenses in contact. It can be shown that the same formula works for thick lenses if d is taken as the distance between their principal planes.
If the separation distance between two lenses is equal to the sum of their focal lengths (d = f1 + f2), then the FFD and BFD are infinite. This corresponds to a pair of lenses that transforms a parallel (collimated) beam into another collimated beam. This type of system is called an afocal system, since it produces no net convergence or divergence of the beam. Two lenses at this separation form the simplest type of optical telescope. Although the system does not alter the divergence of a collimated beam, it does alter the (transverse) width of the beam. The magnification of such a telescope is given by
which is the ratio of the output beam width to the input beam width. Note the sign convention: a telescope with two convex lenses (f1 > 0, f2 > 0) produces a negative magnification, indicating an inverted image. A convex plus a concave lens (f1 > 0 > f2) produces a positive magnification and the image is upright. For further information on simple optical telescopes, see Refracting telescope § Refracting telescope designs.
Non spherical types

Cylindrical lenses have curvature along only one axis. They are used to focus light into a line, or to convert the elliptical light from a laser diode into a round beam. They are also used in motion picture anamorphic lenses.
Aspheric lenses have at least one surface that is neither spherical nor cylindrical. The more complicated shapes allow such lenses to form images with less aberration than standard simple lenses, but they are more difficult and expensive to produce. These were formerly complex to make and often extremely expensive, but advances in technology have greatly reduced the manufacturing cost for such lenses.

A Fresnel lens has its optical surface broken up into narrow rings, allowing the lens to be much thinner and lighter than conventional lenses. Durable Fresnel lenses can be molded from plastic and are inexpensive.
Lenticular lenses are arrays of microlenses that are used in lenticular printing to make images that have an illusion of depth or that change when viewed from different angles.
Bifocal lens has two or more, or a graduated, focal lengths ground into the lens.
A gradient index lens has flat optical surfaces, but has a radial or axial variation in index of refraction that causes light passing through the lens to be focused.
An axicon has a conical optical surface. It images a point source into a line along the optic axis, or transforms a laser beam into a ring.
Diffractive optical elements can function as lenses.
Superlenses are made from negative index metamaterials and claim to produce images at spatial resolutions exceeding the diffraction limit. The first superlenses were made in 2004 using such a metamaterial for microwaves. Improved versions have been made by other researchers. As of 2014 the superlens has not yet been demonstrated at visible or near-infrared wavelengths.
A prototype flat ultrathin lens, with no curvature has been developed.
Uses

A single convex lens mounted in a frame with a handle or stand is a magnifying glass.
Lenses are used as prosthetics for the correction of refractive errors such as myopia, hypermetropia, presbyopia, and astigmatism. (See corrective lens, contact lens, eyeglasses, intraocular lens.) Most lenses used for other purposes have strict axial symmetry; eyeglass lenses are only approximately symmetric. They are usually shaped to fit in a roughly oval, not circular, frame; the optical centres are placed over the eyeballs; their curvature may not be axially symmetric to correct for astigmatism. Sunglasses' lenses are designed to attenuate light; sunglass lenses that also correct visual impairments can be custom made.
Other uses are in imaging systems such as monoculars, binoculars, telescopes, microscopes, cameras and projectors. Some of these instruments produce a virtual image when applied to the human eye; others produce a real image that can be captured on photographic film or an optical sensor, or can be viewed on a screen. In these devices lenses are sometimes paired up with curved mirrors to make a catadioptric system where the lens's spherical aberration corrects the opposite aberration in the mirror (such as Schmidt and meniscus correctors).
Convex lenses produce an image of an object at infinity at their focus; if the sun is imaged, much of the visible and infrared light incident on the lens is concentrated into the small image. A large lens creates enough intensity to burn a flammable object at the focal point. Since ignition can be achieved even with a poorly made lens, lenses have been used as burning-glasses for at least 2400 years. A modern application is the use of relatively large lenses to concentrate solar energy on relatively small photovoltaic cells, harvesting more energy without the need to use larger and more expensive cells.
Radio astronomy and radar systems often use dielectric lenses, commonly called a lens antenna to refract electromagnetic radiation into a collector antenna.
Lenses can become scratched and abraded. Abrasion-resistant coatings are available to help control this.
See also
- Anti-fogging treatment of optical surfaces
- Back focal plane
- Bokeh
- Cardinal point (optics)
- Caustic (optics)
- Eyepiece
- F-number
- Gravitational lens
- Lens (anatomy)
- List of lens designs
- Numerical aperture
- Optical coatings
- Optical lens design
- Photochromic lens
- Prism (optics)
- Ray tracing
- Ray transfer matrix analysis
Notes
- The variant spelling lense is sometimes seen. While it is listed as an alternative spelling in some dictionaries, most mainstream dictionaries do not list it as acceptable.
- Brians, Paul (2003). Common Errors in English. Franklin, Beedle & Associates. p. 125. ISBN 978-1-887902-89-2. Retrieved 28 June 2009. Reports "lense" as listed in some dictionaries, but not generally considered acceptable.
- Merriam-Webster's Medical Dictionary. Merriam-Webster. 1995. p. 368. ISBN 978-0-87779-914-6. Lists "lense" as an acceptable alternate spelling.
- "Lens or Lense – Which is Correct?". writingexplained.org. 30 April 2017. Archived from the original on 21 April 2018. Retrieved 21 April 2018. Analyses the almost negligible frequency of use and concludes that the misspelling is a result of a wrong singularisation of the plural (lenses).
References
- Sines, George; Sakellarakis, Yannis A. (1987). "Lenses in antiquity". American Journal of Archaeology. 91 (2): 191–196. doi:10.2307/505216. JSTOR 505216. S2CID 191384703.
- Whitehouse, David (1 July 1999). "World's oldest telescope?". BBC News. Archived from the original on 1 February 2009. Retrieved 10 May 2008.
- "The Nimrud lens/The Layard lens". Collection database. The British Museum. Archived from the original on 19 October 2012. Retrieved 25 November 2012.
- D. Brewster (1852). "On an account of a rock-crystal lens and decomposed glass found in Niniveh". Die Fortschritte der Physik (in German). Deutsche Physikalische Gesellschaft. p. 355.
- Kriss, Timothy C.; Kriss, Vesna Martich (April 1998). "History of the Operating Microscope: From Magnifying Glass to Microneurosurgery". Neurosurgery. 42 (4): 899–907. doi:10.1097/00006123-199804000-00116. PMID 9574655.
- ^ Aristophanes (22 January 2013) . The Clouds. Translated by Hickie, William James. Project Gutenberg. EBook #2562. Archived 28 June 2017 at the Wayback Machine
- Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 10 Archived 4 October 2008 at the Wayback Machine.
- Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 16 Archived 28 September 2008 at the Wayback Machine
- Tilton, Buck (2005). The Complete Book of Fire: Building Campfires for Warmth, Light, Cooking, and Survival. Menasha Ridge Press. p. 25. ISBN 978-0-89732-633-9.
- Glick, Thomas F.; Steven John Livesey; Faith Wallis (2005). Medieval science, technology, and medicine: an encyclopedia. Routledge. p. 167. ISBN 978-0-415-96930-7. Archived from the original on 20 January 2023. Retrieved 24 April 2011.
- Al Van Helden. The Galileo Project > Science > The Telescope Archived 23 June 2004 at the Wayback Machine. Galileo.rice.edu. Retrieved on 6 June 2012.
- Henry C. King (28 September 2003). The History of the Telescope. Courier Dover Publications. p. 27. ISBN 978-0-486-43265-6. Archived from the original on 2 July 2023. Retrieved 6 June 2012.
- Paul S. Agutter; Denys N. Wheatley (12 December 2008). Thinking about Life: The History and Philosophy of Biology and Other Sciences. Springer. p. 17. ISBN 978-1-4020-8865-0. Retrieved 6 June 2012.
- Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. p. 210. ISBN 978-0-87169-259-7. Retrieved 6 June 2012.
- Microscopes: Time Line Archived 9 January 2010 at the Wayback Machine, Nobel Foundation. Retrieved 3 April 2009
- Fred Watson (1 October 2007). Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 55. ISBN 978-1-74175-383-7. Retrieved 6 June 2012.
- This paragraph is adapted from the 1888 edition of the Encyclopædia Britannica.
- Julia, Elton (18 July 2013). "A Light to Lighten our Darkenss: Lighthouse Optics and the Later Development of Fresnel's Revolutionary Refracting Lens 1780-1900". The International Journal for the History of Engineering & Technology. 79 (2): 72–76. doi:10.1179/175812109X449612 – via Taylor & Francis.
- "4.4: Spherical Refractors". Physics LibreTexts. 2 July 2019. Archived from the original on 26 November 2022. Retrieved 2 July 2023.
- "Refraction at Spherical Surfaces". personal.math.ubc.ca. Archived from the original on 26 October 2021. Retrieved 2 July 2023.
- Hecht, Eugene (2017). "5.2.2 Refraction at Spherical Surfaces". Optics (5th ed.). Pearson. p. 164. ISBN 978-1-292-09693-3.
- Greivenkamp 2004, p. 14
Hecht 1987, § 6.1 - ^ Hecht, Eugene (2017). "Chapter 6.1 Thick Lenses and Lens Systems". Optics (5th ed.). Pearson. ISBN 978-1-292-09693-3.
- "Rule sign for concave and convex lens?". Physics Stack Exchange. Retrieved 27 October 2024.
- ^ Hecht, Eugene (2017). "Finite Imagery". Optics (5th ed.). Pearson. ISBN 978-1-292-09693-3.
- ^ Hecht, Eugene (2017). "Thin-Lens Equations". Optics (5th ed.). Pearson. ISBN 978-1-292-09693-3.
- Nave, Carl R. "Thin Lens Equation". Hyperphysics. Georgia State University. Archived from the original on 12 October 2000. Retrieved 17 March 2015.
- Colwell, Catharine H. "Resource Lesson: Thin Lens Equation". PhysicsLab.org. Archived from the original on 2 April 2015. Retrieved 17 March 2015.
- "The Mathematics of Lenses". The Physics Classroom. Archived from the original on 10 March 2015. Retrieved 17 March 2015.
- There are always 3 "easy rays". For the third ray in this case, see File:Lens3b third ray.svg.
- Hecht, Eugene (2017). "Thin-Lens Combinations". Optics (5th ed.). Pearson. p. 178. ISBN 978-1-292-09693-3.
- Vlasenko, Alexey (2011). "Lecture 9 Notes: 07 / 13 - Multiple-lens systems" (PDF). Physics 1C, Summer Session I, 2011 - University of California San Diego. Archived (PDF) from the original on 18 April 2024. Retrieved 19 April 2024.
- Paschotta, Dr Rüdiger. "focal distance". www.rp-photonics.com. doi:10.61835/6as. Archived from the original on 29 April 2024. Retrieved 29 April 2024.
- Hecht, Eugene (2017). "Back and Front Focal Lengths". Optics (5th ed.). Pearson. p. 181. ISBN 978-1-292-09693-3.
- Proteep Mallik (2005). "The Axicon" (PDF). Archived from the original (PDF) on 23 November 2009. Retrieved 22 November 2007.
- ^ Grbic, A.; Eleftheriades, G. V. (2004). "Overcoming the Diffraction Limit with a Planar Left-handed Transmission-line Lens". Physical Review Letters. 92 (11): 117403. Bibcode:2004PhRvL..92k7403G. doi:10.1103/PhysRevLett.92.117403. PMID 15089166.
- Valentine, J.; et al. (2008). "Three-dimensional optical metamaterial with a negative refractive index". Nature. 455 (7211): 376–9. Bibcode:2008Natur.455..376V. doi:10.1038/nature07247. PMID 18690249. S2CID 4314138.
- Yao, Jie; Liu, Zhaowei; Liu, Yongmin; Wang, Yuan; Sun, Cheng; Bartal, Guy; Stacy, Angelica M.; Zhang, Xiang (15 August 2008). "Optical Negative Refraction in Bulk Metamaterials of Nanowires". Science. 321 (5891): 930. Bibcode:2008Sci...321..930Y. CiteSeerX 10.1.1.716.4426. doi:10.1126/science.1157566. ISSN 0036-8075. PMID 18703734. S2CID 20978013.
- Nielsen, R.B.; Thoreson, M.D.; Chen, W.; Kristensen, A.; Hvam, J.M.; Shalaev, V. M.; Boltasseva, A. (2010). "Toward superlensing with metal–dielectric composites and multilayers" (PDF). Applied Physics B. 100 (1): 93. Bibcode:2010ApPhB.100...93N. doi:10.1007/s00340-010-4065-z. S2CID 39903291. Archived from the original (PDF) on 9 March 2013.
- Patel, Prachi (2015). "Good-Bye to Curved Lens: New Lens Is Flat". Scientific American. 312 (5): 22. doi:10.1038/scientificamerican0515-22b. PMID 26336702. Archived from the original on 19 May 2015. Retrieved 16 May 2015.
- Schottner, G (May 2003). "Scratch and Abrasion Resistant Coatings on Plastic Lenses—State of the Art, Current Developments and Perspectives". Journal of Sol-Gel Science and Technology. Vol. 27. pp. 71–79. doi:10.1023/A:1022684011222.
Bibliography
- Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 978-0-201-11609-0. Chapters 5 & 6.
- Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. ISBN 978-0-321-18878-6.
- Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 978-0-8194-5294-8.
External links
- A chapter from an online textbook on refraction and lenses Archived 17 December 2009 at the Wayback Machine
- Thin Spherical Lenses Archived 13 March 2020 at the Wayback Machine (.pdf) on Project PHYSNET Archived 14 May 2017 at the Wayback Machine.
- Lens article at digitalartform.com
- Article on Ancient Egyptian lenses Archived 25 May 2022 at the Wayback Machine
- FDTD Animation of Electromagnetic Propagation through Convex Lens (on- and off-axis) Video on YouTube
- The Use of Magnifying Lenses in the Classical World Archived 13 November 2017 at the Wayback Machine
- Henker, Otto (1911). "Lens" . Encyclopædia Britannica. Vol. 16 (11th ed.). pp. 421–427. (with 21 diagrams)
Simulations
- Learning by Simulations Archived 21 January 2010 at the Wayback Machine – Concave and Convex Lenses
- OpticalRayTracer Archived 6 October 2010 at the Wayback Machine – Open source lens simulator (downloadable java)
- Animations demonstrating lens Archived 4 April 2012 at the Wayback Machine by QED

 is the on-axis (on the optical axis) object distance from the line perpendicular to the axis toward the refraction point on the surface (which height is h), and
is the on-axis (on the optical axis) object distance from the line perpendicular to the axis toward the refraction point on the surface (which height is h), and  is the on-axis image distance from the line. Due to paraxial approximation where the line of h is close to the vertex of the spherical surface meeting the optical axis on the left,
is the on-axis image distance from the line. Due to paraxial approximation where the line of h is close to the vertex of the spherical surface meeting the optical axis on the left,  for the spherical surface. Similarly,
for the spherical surface. Similarly,  .
.


 , and using
, and using 
 of a spherical lens in air or vacuum for paraxial rays can be calculated from the lensmaker's equation:
of a spherical lens in air or vacuum for paraxial rays can be calculated from the lensmaker's equation:
 where
where
 is the
is the  is the (signed, see
is the (signed, see  is the radius of curvature of the lens surface farther from the light source; and
is the radius of curvature of the lens surface farther from the light source; and is the thickness of the lens (the distance along the lens axis between the two
is the thickness of the lens (the distance along the lens axis between the two  is with respect to the
is with respect to the  and
and  with respect to the respective lens vertices are given by the following formulas, where it is a positive value if it is right to the respective vertex.
with respect to the respective lens vertices are given by the following formulas, where it is a positive value if it is right to the respective vertex.


 is positive for converging lenses, and negative for diverging lenses. The
is positive for converging lenses, and negative for diverging lenses. The  is the
is the 
 as its vertex) images an on-axis object point O to the virtual image I, which can be described by the following equation,
as its vertex) images an on-axis object point O to the virtual image I, which can be described by the following equation, For the imaging by second lens surface, by taking the above sign convention,
For the imaging by second lens surface, by taking the above sign convention,  and
and  Adding these two equations yields
Adding these two equations yields  For the thin lens approximation where
For the thin lens approximation where  the 2nd term of the RHS (Right Hand Side) is gone, so
the 2nd term of the RHS (Right Hand Side) is gone, so




 can be assumed,
can be assumed, 
 is dropped.
is dropped.


 and
and 
 is positive if it is left to the front focal point
is positive if it is left to the front focal point  , and
, and  is positive if it is right to the rear focal point
is positive if it is right to the rear focal point  . Because
. Because  is positive, an object point and the corresponding imaging point made by a lens are always in opposite sides with respect to their respective focal points. (
is positive, an object point and the corresponding imaging point made by a lens are always in opposite sides with respect to their respective focal points. (
 ,
,  , and
, and  are with respect to the
are with respect to the 













 and
and  , and the image distances as and
, and the image distances as and  and
and  . If the lenses are thin, each satisfies the thin lens formula
. If the lenses are thin, each satisfies the thin lens formula

 , then
, then  . (The 2nd lens images the image of the first lens.)
. (The 2nd lens images the image of the first lens.)
 . So, the thin lens formula for the 1st lens becomes
. So, the thin lens formula for the 1st lens becomes


 ). Then the combined focal length f of the lenses is given by
). Then the combined focal length f of the lenses is given by


 is the number of lenses.
is the number of lenses.

