In geometry, demihypercubes (also called n-demicubes, n-hemicubes, and half measure polytopes) are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγn for being half of the hypercube family, γn. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n (n−1)-demicubes, and 2 (n−1)-simplex facets are formed in place of the deleted vertices.
They have been named with a demi- prefix to each hypercube name: demicube, demitesseract, etc. The demicube is identical to the regular tetrahedron, and the demitesseract is identical to the regular 16-cell. The demipenteract is considered semiregular for having only regular facets. Higher forms do not have all regular facets but are all uniform polytopes.
The vertices and edges of a demihypercube form two copies of the halved cube graph.
An n-demicube has inversion symmetry if n is even.
Discovery
Thorold Gosset described the demipenteract in his 1900 publication listing all of the regular and semiregular figures in n-dimensions above three. He called it a 5-ic semi-regular. It also exists within the semiregular k21 polytope family.
The demihypercubes can be represented by extended Schläfli symbols of the form h{4,3,...,3} as half the vertices of {4,3,...,3}. The vertex figures of demihypercubes are rectified n-simplexes.
Constructions
They are represented by Coxeter-Dynkin diagrams of three constructive forms:




 ...
... (As an alternated orthotope) s{2}
(As an alternated orthotope) s{2}


 ...
...
 (As an alternated hypercube) h{4,3}
(As an alternated hypercube) h{4,3}


 ...
...
 . (As a demihypercube) {3}
. (As a demihypercube) {3}
H.S.M. Coxeter also labeled the third bifurcating diagrams as 1k1 representing the lengths of the three branches and led by the ringed branch.
An n-demicube, n greater than 2, has n(n−1)/2 edges meeting at each vertex. The graphs below show less edges at each vertex due to overlapping edges in the symmetry projection.
| n | 1k1 | Petrie polygon |
Schläfli symbol | Coxeter diagrams A1 Bn Dn |
Elements | Facets: Demihypercubes & Simplexes |
Vertex figure | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | 8-faces | 9-faces | |||||||
| 2 | 1−1,1 | demisquare (digon) 
|
s{2} h{4} {3} |
2 | 2 | 2 edges |
-- | |||||||||
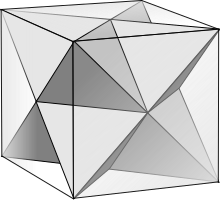
| 3 | 101 | demicube (tetrahedron) 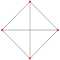 
|
s{2} h{4,3} {3} |
4 | 6 | 4 | (6 digons) 4 triangles |
Triangle (Rectified triangle) | ||||||||
| 4 | 111 | demitesseract (16-cell)  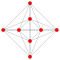
|
s{2} h{4,3,3} {3} |
8 | 24 | 32 | 16 | 8 demicubes (tetrahedra) 8 tetrahedra |
Octahedron (Rectified tetrahedron) | |||||||
| 5 | 121 | demipenteract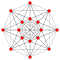 
|
s{2} h{4,3}{3} |
16 | 80 | 160 | 120 | 26 | 10 16-cells 16 5-cells |
Rectified 5-cell | ||||||
| 6 | 131 | demihexeract 
|
s{2} h{4,3}{3} |
32 | 240 | 640 | 640 | 252 | 44 | 12 demipenteracts 32 5-simplices |
Rectified hexateron | |||||
| 7 | 141 | demihepteract 
|
s{2} h{4,3}{3} |
64 | 672 | 2240 | 2800 | 1624 | 532 | 78 | 14 demihexeracts 64 6-simplices |
Rectified 6-simplex | ||||
| 8 | 151 | demiocteract 
|
s{2} h{4,3}{3} |
128 | 1792 | 7168 | 10752 | 8288 | 4032 | 1136 | 144 | 16 demihepteracts 128 7-simplices |
Rectified 7-simplex | |||
| 9 | 161 | demienneract 
|
s{2} h{4,3}{3} |
256 | 4608 | 21504 | 37632 | 36288 | 23520 | 9888 | 2448 | 274 | 18 demiocteracts 256 8-simplices |
Rectified 8-simplex | ||
| 10 | 171 | demidekeract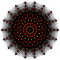 
|
s{2} h{4,3}{3} |
512 | 11520 | 61440 | 122880 | 142464 | 115584 | 64800 | 24000 | 5300 | 532 | 20 demienneracts 512 9-simplices |
Rectified 9-simplex | |
| ... | ||||||||||||||||
| n | 1n−3,1 | n-demicube | s{2} h{4,3}{3} |
2 | 2n (n−1)-demicubes 2 (n−1)-simplices |
Rectified (n−1)-simplex | ||||||||||
In general, a demicube's elements can be determined from the original n-cube: (with Cn,m = m-face count in n-cube = 2 n!/(m!(n−m)!))
- Vertices: Dn,0 = 1/2 Cn,0 = 2 (Half the n-cube vertices remain)
- Edges: Dn,1 = Cn,2 = 1/2 n(n−1) 2 (All original edges lost, each square faces create a new edge)
- Faces: Dn,2 = 4 * Cn,3 = 2/3 n(n−1)(n−2) 2 (All original faces lost, each cube creates 4 new triangular faces)
- Cells: Dn,3 = Cn,3 + 2 Cn,4 (tetrahedra from original cells plus new ones)
- Hypercells: Dn,4 = Cn,4 + 2 Cn,5 (16-cells and 5-cells respectively)
- ...
- : Dn,m = Cn,m + 2 Cn,m+1 (m-demicubes and m-simplexes respectively)
- ...
- Facets: Dn,n−1 = 2n + 2 ((n−1)-demicubes and (n−1)-simplices respectively)
Symmetry group
The stabilizer of the demihypercube in the hyperoctahedral group (the Coxeter group ) has index 2. It is the Coxeter group of order , and is generated by permutations of the coordinate axes and reflections along pairs of coordinate axes.
Orthotopic constructions

Constructions as alternated orthotopes have the same topology, but can be stretched with different lengths in n-axes of symmetry.
The rhombic disphenoid is the three-dimensional example as alternated cuboid. It has three sets of edge lengths, and scalene triangle faces.
See also
References
- Regular and semi-regular polytopes III, p. 315-316
- "week187". math.ucr.edu. Retrieved 20 April 2018.
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
External links
- Olshevsky, George. "Half measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
| Dimension | ||
|---|---|---|
| Dimensional spaces |  | |
| Other dimensions | ||
| Polytopes and shapes | ||
| Number systems | ||
| Dimensions by number | ||
| See also | ||
| Category | ||
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 ) has index 2. It is the Coxeter group
) has index 2. It is the Coxeter group  of order
of order  , and is generated by permutations of the coordinate axes and reflections along pairs of coordinate axes.
, and is generated by permutations of the coordinate axes and reflections along pairs of coordinate axes.