| Revision as of 07:29, 21 April 2013 editIncnis Mrsi (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers11,646 edits tweaks, →Polytopes in Rn: added some analytic/set theoretical perspective to overcome my strong initial geometric/algebraic bias← Previous edit | Revision as of 13:01, 21 April 2013 edit undoIncnis Mrsi (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers11,646 edits +Next edit → | ||
| Line 15: | Line 15: | ||
| Purely mathematical uses of {{math|'''R'''<sup>''n''</sup>}} can be roughly classified as follows, although these uses overlap. First, ] studies its own properties under ] and ]s and use in as a model of any {{mvar|n}}-] real ]. Second, it is used in ] to represent the ] of a ] of {{mvar|n}} real variables in an uniform way, as well as a space to which the ] of a real-valued function of {{math|''n'' − 1}} real variables is a subset. The third use parametrizes ] with elements of {{math|'''R'''<sup>''n''</sup>}}; it is common in ], ] and ] geometries. | Purely mathematical uses of {{math|'''R'''<sup>''n''</sup>}} can be roughly classified as follows, although these uses overlap. First, ] studies its own properties under ] and ]s and use in as a model of any {{mvar|n}}-] real ]. Second, it is used in ] to represent the ] of a ] of {{mvar|n}} real variables in an uniform way, as well as a space to which the ] of a real-valued function of {{math|''n'' − 1}} real variables is a subset. The third use parametrizes ] with elements of {{math|'''R'''<sup>''n''</sup>}}; it is common in ], ] and ] geometries. | ||
| {{math|'''R'''<sup>''n''</sup>}}, together with supplemental structures on it, is also extensively used in ], ], ] and ]. | |||
| ⚫ | ], ]s, and other collections of ]s in applications can be seen as the use of {{math|'''R'''<sup>''n''</sup>}} too. | ||
| ⚫ | In ], ], and so on, ], ]s, and other collections of ]s in applications can be seen as the use of {{math|'''R'''<sup>''n''</sup>}} too. | ||
| == Vector space == | == Vector space == | ||
| Line 37: | Line 39: | ||
| :<math>\mathbf x = \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix}.</math> | :<math>\mathbf x = \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix}.</math> | ||
| The coordinate space {{math|'''R'''<sup>''n''</sup>}} may then be interpreted as the space of all {{math|''n'' × 1}} ]s, or all {{math|1 × ''n''}} ]s with the ordinary matrix operations of addition and scalar multiplication. | The coordinate space {{math|'''R'''<sup>''n''</sup>}} may then be interpreted as the space of all {{math|''n'' × 1}} ]s, or all {{math|1 × ''n''}} ]s with the ordinary matrix operations of addition and ]. | ||
| ]s from {{math|'''R'''<sup>''n''</sup>}} to {{math|'''R'''<sup>''m''</sup>}} may then be written as {{math|''m'' × ''n''}} matrices which act on the elements of {{math|'''R'''<sup>''n''</sup>}} via ] multiplication (when the elements of {{math|'''R'''<sup>''n''</sup>}} are column vectors) and on elements of {{math|'''R'''<sup>''m''</sup>}} via right multiplication (when they are row vectors). | ]s from {{math|'''R'''<sup>''n''</sup>}} to {{math|'''R'''<sup>''m''</sup>}} may then be written as {{math|''m'' × ''n''}} matrices which act on the elements of {{math|'''R'''<sup>''n''</sup>}} via ] multiplication (when the elements of {{math|'''R'''<sup>''n''</sup>}} are column vectors) and on elements of {{math|'''R'''<sup>''m''</sup>}} via right multiplication (when they are row vectors). The formula for left multiplication, a special case of ], is: | ||
| :<math>(A{\mathbf x})_k = \sum\limits_{l=1}^n A_{kl} x_l</math> | |||
| {{anchor|continuity of linear maps}}Any linear transformation is a ] (see ]). Also, a matrix define an ] from {{math|'''R'''<sup>''n''</sup>}} to {{math|'''R'''<sup>''m''</sup>}} if and only if the ] equals to {{mvar|m}}. | {{anchor|continuity of linear maps}}Any linear transformation is a ] (see ]). Also, a matrix define an ] from {{math|'''R'''<sup>''n''</sup>}} to {{math|'''R'''<sup>''m''</sup>}} if and only if the ] equals to {{mvar|m}}. | ||
| Line 63: | Line 66: | ||
| == Geometric properties and uses == | == Geometric properties and uses == | ||
| === Orientation === | === Orientation === | ||
| The fact that ], unlike many other ], constitute an ] yields an] on {{math|'''R'''<sup>''n''</sup>}}. Any ] linear map of {{math|'''R'''<sup>''n''</sup>}} to itself either preserves or reverses orientation of the space depending on the ] of the ] of its matrix. If one ] coordinates (or, in other words, elements of the basis), the resulting orientation will depend on the ]. | The fact that ], unlike many other ], constitute an ] yields an ] on {{math|'''R'''<sup>''n''</sup>}}. Any ] linear map of {{math|'''R'''<sup>''n''</sup>}} to itself either preserves or reverses orientation of the space depending on the ] of the ] of its matrix. If one ] coordinates (or, in other words, elements of the basis), the resulting orientation will depend on the ]. | ||
| ]s of {{math|'''R'''<sup>''n''</sup>}} or ], by their virtue to avoid zero ], are also classified to orientation-preserving and orientation-reversing. It has important consequences for the theory of ]s, whose applications include ]. | ]s of {{math|'''R'''<sup>''n''</sup>}} or ], by their virtue to avoid zero ], are also classified to orientation-preserving and orientation-reversing. It has important consequences for the theory of ]s, whose applications include ]. | ||
| Line 87: | Line 90: | ||
| Although the definition of a ] does not require that its model space should be {{math|'''R'''<sup>''n''</sup>}}, this choice is the most common, and almost exclusive one in ]. | Although the definition of a ] does not require that its model space should be {{math|'''R'''<sup>''n''</sup>}}, this choice is the most common, and almost exclusive one in ]. | ||
| On the other hand, ]s state that any {{mvar|m}}-dimensional manifold can be ] into {{math|'''R'''<sup>2''m''</sup>}}. | On the other hand, ]s state that any real ] can be ] into {{math|'''R'''<sup>2''m''</sup>}}. | ||
| {{expand section|date=April 2013}} | {{expand section|date=April 2013}} | ||
| === Other appearances === | === Other appearances === | ||
| Other structures considered on {{math|'''R'''<sup>''n''</sup>}} include the one of a ]. | Other structures considered on {{math|'''R'''<sup>''n''</sup>}} include the one of a ] and ]. | ||
| {{expand section|date=April 2013}} | {{expand section|date=April 2013}} | ||
| Line 126: | Line 129: | ||
| == Topological properties == | == Topological properties == | ||
| The ] of {{math|'''R'''<sup>''n''</sup>}} (called '''standard topology''', '''Euclidean topology''', or '''usual topology''') can be obtained not only from Cartesian product. It is also identical to the ] induced by ]: a set is ] in the Euclidean topology ] it contains an ] around each of its points. Also, {{math|'''R'''<sup>''n''</sup>}} is a ] (see ] above), and there is only one possible (non-trivial) topology compatible with its linear structure. As there are many open linear maps from {{math|'''R'''<sup>''n''</sup>}} to itself which are not ], there can be many Euclidean structures on {{math|'''R'''<sup>''n''</sup>}} which correspond to the same topology. Actually, it does not depend much even on the linear structure: there are many non-linear ]s (and other homeomorphisms) of {{math|'''R'''<sup>''n''</sup>}} onto itself, or its parts. | The ] of {{math|'''R'''<sup>''n''</sup>}} (called '''standard topology''', '''Euclidean topology''', or '''usual topology''') can be obtained not only from Cartesian product. It is also identical to the ] induced by ]: a set is ] in the Euclidean topology ] it contains an ] around each of its points. Also, {{math|'''R'''<sup>''n''</sup>}} is a ] (see ] above), and there is only one possible (non-trivial) topology compatible with its linear structure. As there are many open linear maps from {{math|'''R'''<sup>''n''</sup>}} to itself which are not ], there can be many Euclidean structures on {{math|'''R'''<sup>''n''</sup>}} which correspond to the same topology. Actually, it does not depend much even on the linear structure: there are many non-linear ]s (and other homeomorphisms) of {{math|'''R'''<sup>''n''</sup>}} onto itself, or its parts such as an Euclidean ] or ]). | ||
| {{math|'''R'''<sup>''n''</sup>}} has the ] {{mvar|n}}. | {{math|'''R'''<sup>''n''</sup>}} has the ] {{mvar|n}}. | ||
| <!-- The initial (16 April, 2013) revision of this section used a content from the ] article. See the history there for attribution. --> | <!-- The initial (16 April, 2013) revision of this section used a content from the ] article. See the history there for attribution. --> | ||
| An important result on the topology of {{math|'''R'''<sup>''n''</sup>}}, that is far from superficial, is ]'s ]. Any subset of {{math|'''R'''<sup>''n''</sup>}} (with its ]) that is ] to another open subset of {{math|'''R'''<sup>''n''</sup>}} is itself open. An immediate consequence of this is that {{math|'''R'''<sup>''m''</sup>}} is not ] to {{math|'''R'''<sup>''n''</sup>}} if {{math|''m'' ≠ ''n''}} – an intuitively "obvious" result which is nonetheless difficult to prove. | An important result on the topology of {{math|'''R'''<sup>''n''</sup>}}, that is far from superficial, is ]'s ]. Any subset of {{math|'''R'''<sup>''n''</sup>}} (with its ]) that is ] to another open subset of {{math|'''R'''<sup>''n''</sup>}} is itself open. An immediate consequence of this is that {{math|'''R'''<sup>''m''</sup>}} is not ] to {{math|'''R'''<sup>''n''</sup>}} if {{math|''m'' ≠ ''n''}} – an intuitively "obvious" result which is nonetheless difficult to prove. | ||
| Despite the difference in topological dimension, and contrary to a naïve perception, it is possible to map a lesser-dimensional real space continuously and ] onto {{math|'''R'''<sup>''n''</sup>}}. A continuous (although not smooth) ] (an image of {{math|'''R'''<sup>1</sup>}}) is possible. | |||
| == Examples == | == Examples == | ||
| Line 158: | Line 163: | ||
| {{math|'''R'''<sup>4</sup>}} can be imagined using the fact that {{num|16}} points {{math|(''x''<sub>1</sub>, ''x''<sub>2</sub>, ''x''<sub>3</sub>, ''x''<sub>4</sub>)}}, where each {{mvar|x<sub>k</sub>}} is either 0 or 1, are vertices of a ] (pictured), the 4-hypercube (see ]). | {{math|'''R'''<sup>4</sup>}} can be imagined using the fact that {{num|16}} points {{math|(''x''<sub>1</sub>, ''x''<sub>2</sub>, ''x''<sub>3</sub>, ''x''<sub>4</sub>)}}, where each {{mvar|x<sub>k</sub>}} is either 0 or 1, are vertices of a ] (pictured), the 4-hypercube (see ]). | ||
| ⚫ | The first major use of {{math|'''R'''<sup>4</sup>}} is a ] model: three spacial coordinates plus one ]. This is usually associated with ], although four dimensions were continuously used for such models since ]. The choice of theory leads to different structure, though: in ] the {{mvar|t}} coordinate is privileged, but in Einsteinian relativity it is not. Special relativity is set in ]. General relativity uses curved spaces, which may be thought of as {{math|'''R'''<sup>4</sup>}} with a ] for most practical purposes, though. Any of these structures does not provide a (positive) ] on {{math|'''R'''<sup>4</sup>}}. | ||
| There are two major uses of {{math|'''R'''<sup>4</sup>}}. | |||
| ⚫ | The first |
||
| Euclidean {{math|'''R'''<sup>4</sup>}} also attracts the attention of mathematicians, for example due to its relation to ]s. See ] for some information. | Euclidean {{math|'''R'''<sup>4</sup>}} also attracts the attention of mathematicians, for example due to its relation to ]s. See ] for some information. | ||
| In differential geometry, {{math|1=''n'' = 4}} is the only case where {{math|'''R'''<sup>''n''</sup>}} admits a non-standard ]: see ]. | |||
| == Generalizations == | == Generalizations == | ||
Revision as of 13:01, 21 April 2013
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Real coordinate space" – news · newspapers · books · scholar · JSTOR (April 2013) (Learn how and when to remove this message) |

In mathematics, real coordinate space of n dimensions, written R (R with superscript n, also written ℝ with blackboard bold R) is a coordinate space that allows several (n) real variables to be treated as a single variable. With various numbers of dimensions (sometimes unspecified), R is used in many areas of pure and applied mathematics, as well as in physics. It is the prototypical real vector space and a frequently used representation of Euclidean n-space. Due to the latter fact, geometric metaphors are widely used for R, namely a plane for R and three-dimensional space for R.
Definition and uses
For any natural number n, the set R consists of all n-tuples of real numbers (R). It is called (the) "n-dimensional real space". As it can be constructed as Cartesian product of n instances of the set R, it inherits some of its structure, notably:
- R has addition and scalar multiplication: see below
- R is a topological space: see below
An element of R is written
where each xi is a real number.
For each n there exists only one R, the real n-space.
Purely mathematical uses of R can be roughly classified as follows, although these uses overlap. First, linear algebra studies its own properties under vector addition and linear transformations and use in as a model of any n-dimensional real vector space. Second, it is used in mathematical analysis to represent the domain of a function of n real variables in an uniform way, as well as a space to which the graph of a real-valued function of n − 1 real variables is a subset. The third use parametrizes geometric points with elements of R; it is common in analytic, differential and algebraic geometries.
R, together with supplemental structures on it, is also extensively used in mathematical physics, dynamical systems theory, mathematical statistics and probability theory.
In applied mathematics, numerical analysis, and so on, arrays, sequences, and other collections of numbers in applications can be seen as the use of R too.
Vector space
See also: Basis (linear algebra)R forms an n-dimensional vector space over the field of real numbers. The operations on R are defined by
The zero vector is given by
and the additive inverse of the vector x is given by
Matrix notation
Main article: Matrix (mathematics)In standard matrix notation, each element of R is typically written as a column vector
and sometimes as a row vector:
The coordinate space R may then be interpreted as the space of all n × 1 column vectors, or all 1 × n row vectors with the ordinary matrix operations of addition and scalar multiplication.
Linear transformations from R to R may then be written as m × n matrices which act on the elements of R via left multiplication (when the elements of R are column vectors) and on elements of R via right multiplication (when they are row vectors). The formula for left multiplication, a special case of matrix multiplication, is:
Any linear transformation is a continuous function (see below). Also, a matrix define an open map from R to R if and only if the rank of the matrix equals to m.
Standard basis
Main article: Standard basisThe coordinate space R comes with a standard basis:
To see that this is a basis, note that an arbitrary vector in R can be written uniquely in the form
Geometric properties and uses
Orientation
The fact that real numbers, unlike many other fields, constitute an ordered field yields an orientation structure on R. Any full-rank linear map of R to itself either preserves or reverses orientation of the space depending on the sign of the determinant of its matrix. If one permutes coordinates (or, in other words, elements of the basis), the resulting orientation will depend on the parity of the permutation.
Diffeomorphisms of R or domains in it, by their virtue to avoid zero Jacobian, are also classified to orientation-preserving and orientation-reversing. It has important consequences for the theory of differential forms, whose applications include electrodynamics.
Another manifestation of this structure is that the point reflection in R has different properties depending on evenness of n. For even n it preserves orientation, while for odd n it is reversed (see also improper rotation).
Affine space
Main article: Affine spaceR understood as an affine space is the same space, where R as a vector space acts by translations. Conversely, a vector has to be understood as a "difference between two points", usually illustrated by a directed line segment connecting two points. The distinction says that there is no canonical choice of where the origin should go in an affine n-space, because it can be translated anywhere.
Euclidean space
Main articles: Euclidean space and Cartesian coordinate systemThe dot product
defines the norm | x | =√x⋅x on the vector space R. If every vector has its Euclidean norm, then for any pair of points the distance
is defined, providing a metric space structure on R in addition to its affine structure.
Like for vector space structure, the dot product and Euclidean distance usually are assumed existing on R without special explanations. Though, the real n-space and an Euclidean n-space are distinct objects, strictly speaking. Any Euclidean n-space has a coordinate system where dot product and Euclidean distance have the form shown above, called Cartesian. But there are many Cartesian coordinate systems on an Euclidean space. Conversely, the formula for Euclidean metric above defines the standard Euclidean structure on R, but it is not the only possible one. In spite of this clauses, concepts of R and of an Euclidean n-space are not always distinguished even in professional mathematical works.
In algebraic and differential geometry
Although the definition of a manifold does not require that its model space should be R, this choice is the most common, and almost exclusive one in differential geometry.
On the other hand, Whitney embedding theorems state that any real differentiable m-dimensional manifold can be embedded into R.
| This section needs expansion. You can help by adding to it. (April 2013) |
Other appearances
Other structures considered on R include the one of a pseudo-Euclidean space and symplectic structure.
| This section needs expansion. You can help by adding to it. (April 2013) |
Polytopes in R
See also: Linear programming and Convex polytopeThere are three families of polytopes which have simple representations in R spaces, for any n, and can be used to visualize any affine coordinate system in a real n-space. Vertices of hypercube have coordinates (x1, x2, … , xn) where each xk is either 0 or 1. Actually, any two numbers can be chosen instead of 0 and 1, for example −1 and 1. An n-hypercube can be thought of as the Cartesian product of n identical intervals (such as the unit interval [0,1]) on the real line. As an n-dimensional subset it can be described with a system of 2n inequalities:
| (for [0,1]) | (for [−1,1]) |
Each vertex of the cross-polytope has, for some k, the xk coordinate equal to ±1 and all other coordinates equal to 0 (such that it is the kth standard basis vector up to sign). This is a dual polytope of hypercube. As an n-dimensional subset it can be described with a single inequality which uses the absolute value operation:
but this can be expressed with a system of 2 linear inequalities as well.
The third polytope with simply enumerable coordinates is the standard simplex, whose vertices are n standard basis vectors and the origin (0, 0, … , 0). As an n-dimensional subset it is described with a system of n + 1 linear inequalities:
Replacement of all "≤" with "<" gives interiors of these polytopes.
Topological properties
The topological structure of R (called standard topology, Euclidean topology, or usual topology) can be obtained not only from Cartesian product. It is also identical to the natural topology induced by Euclidean metric discussed above: a set is open in the Euclidean topology if and only if it contains an open ball around each of its points. Also, R is a linear topological space (see #continuity of linear maps above), and there is only one possible (non-trivial) topology compatible with its linear structure. As there are many open linear maps from R to itself which are not isometries, there can be many Euclidean structures on R which correspond to the same topology. Actually, it does not depend much even on the linear structure: there are many non-linear diffeomorphisms (and other homeomorphisms) of R onto itself, or its parts such as an Euclidean open ball or the interior of a hypercube).
R has the topological dimension n. An important result on the topology of R, that is far from superficial, is Brouwer's invariance of domain. Any subset of R (with its subspace topology) that is homeomorphic to another open subset of R is itself open. An immediate consequence of this is that R is not homeomorphic to R if m ≠ n – an intuitively "obvious" result which is nonetheless difficult to prove.
Despite the difference in topological dimension, and contrary to a naïve perception, it is possible to map a lesser-dimensional real space continuously and surjectively onto R. A continuous (although not smooth) space-filling curve (an image of R) is possible.
Examples
n ≤ 1
| Empty column vector, the only element of R |

Cases of 0 ≤ n ≤ 1 do not offer anything new: R is the real line, whereas R (the space of empty vectors) is a singleton, understood as zero vector space. Though, it is useful to include these "trivial" cases to theories which are appropriate for different n.
n = 2
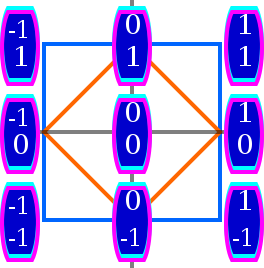
| This section needs expansion. You can help by adding to it. (April 2013) |
n = 3

| This section needs expansion. You can help by adding to it. (April 2013) |
n = 4

R can be imagined using the fact that 16 points (x1, x2, x3, x4), where each xk is either 0 or 1, are vertices of a tesseract (pictured), the 4-hypercube (see above).
The first major use of R is a spacetime model: three spacial coordinates plus one temporal. This is usually associated with theory of relativity, although four dimensions were continuously used for such models since Galilei. The choice of theory leads to different structure, though: in Galilean relativity the t coordinate is privileged, but in Einsteinian relativity it is not. Special relativity is set in Minkowski space. General relativity uses curved spaces, which may be thought of as R with a curved metric for most practical purposes, though. Any of these structures does not provide a (positive) metric on R.
Euclidean R also attracts the attention of mathematicians, for example due to its relation to quaternions. See SO(4) for some information.
In differential geometry, n = 4 is the only case where R admits a non-standard differential structure: see exotic R.
Generalizations
| This section needs expansion. You can help by adding to it. (April 2013) |
See also
- Exponential object, for theoretical explanation of the superscript notation
- Real projective space
Footnotes
- Unlike many situations in mathematics where certain object is unique up to isomorphism, R in unique in the strong sense: any its element is described explicitly with its n real coordinates.
References
- Kelley, John L. (1975). General Topology. Springer-Verlag. ISBN 0-387-90125-6.
- Munkres, James (1999). Topology. Prentice-Hall. ISBN 0-13-181629-2.












 (for [0,1])
(for [0,1])
 (for [−1,1])
(for [−1,1])

