| Revision as of 15:13, 14 January 2008 edit212.24.224.18 (talk) →Arithmetic← Previous edit | Latest revision as of 22:03, 7 January 2025 edit undoKMaster888 (talk | contribs)Extended confirmed users12,260 edits ce | ||
| Line 1: | Line 1: | ||
| {{Short description|none}} <!-- "none" is preferred when the title is sufficiently descriptive; see ] --> | |||
| In the ], '''Islamic mathematics''' or '''Arabic mathematics''' refers to the ] developed in the ] between ] and ]. While most scientists in this period were ]s and ] was the dominant language, contributions were made by people of different ethnic groups (]s, ], ], ]) and religions (]s, ]s, ]s, ]s, ]).<ref>Hogendijk 1999</ref> The center of Islamic mathematics was located in present-day ] and ], but at its greatest extent stretched from ], ] and ] in the west, to ] in the east.<ref>O'Connor 1999</ref> | |||
| {{pp-move-indef|small=yes}} | |||
| ]'' by ]]] | |||
| ] during the ], especially during the 9th and 10th centuries, was built upon syntheses of ] (], ], ]) and ] (], ]). Important developments of the period include extension of the ] to include ], the systematised study of ] and advances in ] and ].<ref>{{harvp|Katz|1993}}: "A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied... Still, the general outline... is known. In particular, Islamic mathematicians fully developed the decimal place-value number system to include decimal fractions, systematised the study of algebra and began to consider the relationship between algebra and geometry, studied and made advances on the major Greek geometrical treatises of Euclid, Archimedes, and Apollonius, and made significant improvements in plane and spherical geometry."<br/> | |||
| ] and mathematics flourished under the Islamic ]ate (also known as the ] or ]) established across the ], ], ], ], the ], and in parts of ] and ] (known as ] at the time) in the 8th century. Although most Islamic texts on mathematics were written in Arabic, they were not all written by ]s, since—much like ] in ]—Arabic was used as the written language of scholars throughout the ] at the time. In particular, a large number of Islamic scientists in many disciplines, including mathematics, were Persians.<ref></ref> | |||
| ^ {{harvp|Smith|1958|loc=Vol. 1, Chapter VII.4}}: "In a general way it may be said that the Golden Age of Arabian mathematics was confined largely to the 9th and 10th centuries; that the world owes a great debt to Arab scholars for preserving and transmitting to posterity the classics of Greek mathematics; and that their work was chiefly that of transmission, although they developed considerable originality in algebra and showed some genius in their work in trigonometry."</ref> | |||
| The ] underwent significant developments in mathematics. ] played a key role in this transformation, introducing algebra as a distinct field in the 9th century. ]'s approach, departing from earlier arithmetical traditions, laid the groundwork for the arithmetization of ], influencing mathematical thought for an extended period. Successors like ] expanded on his work, contributing to advancements in various mathematical domains. The practicality and broad applicability of these mathematical methods facilitated the dissemination of Arabic mathematics to the West, contributing substantially to the evolution of Western mathematics.<ref>{{cite book |last1=Lumpkin |first1=Beatrice |url=https://archive.org/details/goldenageofmoor00vans |title=Golden age of the Moor, Volume 11 |last2=Zitler |first2=Siham |publisher=Transaction Publishers |year=1992 |isbn=1-56000-581-5 |editor-last=Van Sertima |editor-first=Ivan |editor-link=Ivan van Sertima |page= |chapter=Cairo: Science Academy of the Middle Ages}} "The Islamic mathematicians exercised a prolific influence on the development of science in Europe, enriched as much by their own discoveries as those they had inherited by the Greeks, the Indians, the Syrians, the Babylonians, etc."</ref> | |||
| J. J. O'Conner and E. F. Robertson wrote in the '']'': | |||
| {{quote|"Recent research paints a new picture of the debt that we owe to Islamic mathematics. Certainly many of the ideas which were previously thought to have been brilliant new conceptions due to ]an mathematicians of the 16th, 17th, and 18th centuries are now known to have been developed by Arabic/Islamic mathematicians around four centuries earlier. In many respects, the mathematics studied today is far closer in style to that of Islamic mathematics than to that of ]."}} | |||
| Arabic mathematical knowledge spread through various channels during the ], driven by the practical applications of ]'s methods. This dissemination was influenced not only by economic and political factors but also by cultural exchanges, exemplified by events such as the ] and the translation movement. The ], spanning from the 8th to the 14th century, marked a period of considerable advancements in various scientific disciplines, attracting scholars from medieval Europe seeking access to this knowledge. Trade routes and cultural interactions played a crucial role in introducing Arabic mathematical ideas to the West. The translation of Arabic mathematical texts, along with Greek and Roman works, during the 14th to 17th century, played a pivotal role in shaping the intellectual landscape of the ]. | |||
| R. Rashed wrote in ''The development of Arabic mathematics: between arithmetic and algebra'': | |||
| {{quote|"]'s successors undertook a systematic application of ] to ], algebra to arithmetic, both to ], algebra to the ]ean ], algebra to ], and geometry to algebra. This was how the creation of ], ], ], the numerical solution of ]s, the new elementary theory of numbers, and the geometric construction of equations arose."}} | |||
| == Origin and spread of Arab-Islamic mathematics == | |||
| ==Origins and influences == | |||
| Arabic mathematics, particularly algebra, developed significantly during the ]. ]'s ({{Langx|ar|محمد بن موسى الخوارزمي}}; {{Circa|780|850}}) work between AD 813 and 833 in Baghdad was a turning point. He introduced the term "algebra" in the title of his book, "]," marking it as a distinct discipline. He regarded his work as "a short work on Calculation by (the rules of) Completion and Reduction, confining it to what is easiest and most useful in arithmetic".<ref name="ben Musa-2013">{{Cite book |last=ben Musa |first=Mohammed |url=http://dx.doi.org/10.1017/cbo9781139505871 |title=The Algebra of Mohammed ben Musa |date=2013-03-28 |publisher=Cambridge University Press |isbn=978-1-108-05507-9}}</ref> Later, people commented his work was not just a theoretical treatise but also practical, aimed at solving problems in areas like commerce and land measurement. | |||
| The first century of the ]ic ] saw almost no scientific or mathematical achievements since the Arabs, with their newly conquered empire, had not yet gained any intellectual drive and research in other parts of the world had faded. In the second half of the eighth century Islam had a cultural awakening, and research in mathematics and the sciences increased.<ref name="Boyer Intro Islamic Algebra">{{cite book|last=Boyer|authorlink=Carl Benjamin Boyer|title=|year=1991|chapter=The Arabic Hegemony|pages=227|quote=The first century of the Muslim empire had been devoid of scientific achievement. This period (from about 650 to 750) had been, in fact, perhaps the nadir in the development of mathematics, for the Arabs had not yet achieved intellectual drive, and concern for learning in other parts of the world had faded. Had it not been for the sudden cultural awakening in Islam during the second half of the eighth century, considerably more of ancient science and mathematics would have been lost. It was during the caliphate of al-Mamun (809-833), however, that the Arabs fully indulged their passion for translation. The caliph is said to have had a dream in which Aristotle appeared, and as a consequence al-Mamun determined to have Arabic versions made of all the Greek works that he could lay his hands on, including Ptolemy's ''Almagest'' and a complete version of Euclid's ''Elements''. From the Byzantine Empire, with which the Arabs maintained an uneasy peace, Greek manuscripts were obtained through peace treaties. Al-Mamun established at Baghdad a "House of Wisdom" (Bait al-hikma) comparable to the ancient Museum at Alexandria. Among the faculty members was a mathematician and astronomer, Mohammed ibn-Musa al-Khwarizmi, whose name, like that of Euclid, later was to become a household word in Western Europe. The scholar, who died sometime before 850, wrote more than half a dozen astronomical and mathematical works, of which the earliest were probably based on the ''Sindhad'' derived from India.}}</ref> The Muslim ] ] ] (809-833) is said to have had a dream where Aristotle appeared to him, and as a consequence al-Mamun ordered that Arabic translation be made of as many Greek works as possible, including Ptolemy's ''Almagest'' and Euclid's ''Elements''. Greek works would be given to the Muslims by the ] in exchange for treaties, as the two empires held an uneasy peace.<ref name="Boyer Intro Islamic Algebra" /> Many of these Greek works were translated by ] (826-901), who translated books written by ], ], ], ], and Eutocius.<ref name="Boyer Islamic Rhetoric Algebra Thabit">{{cite book|last=Boyer|authorlink=Carl Benjamin Boyer|title=|year=1991|chapter=The Arabic Hegemony|pages=234|quote=but al-Khwarizmi's work had a serious deficiency that had to be removed before it could serve its purpose effectively in the modern world: a symbolic notation had to be developed to replace the rhetorical form. This step the Arabs never took, except for the replacement of number words by number signs. Thabit was the founder of a school of translators, especially from Greek and Syriac, and to him we owe an immense debt for translations into Arabic of works by ], ], ], ], and ].}}</ref> Historians are in debt to many Islamic translators, for it is through their work that many ancient ] texts have survived only through ] translations. | |||
| ]'s approach was groundbreaking in that it did not arise from any previous "arithmetical" tradition, including that of ]. He developed a new vocabulary for algebra, distinguishing between purely algebraic terms and those shared with arithmetic. Al-Khwārizmī noticed that the representation of numbers is crucial in daily life. Thus, he wanted to find or summarize a way to simplify the mathematical operation, so-called later, the algebra.<ref name="ben Musa-2013" /> His algebra was initially focused on linear and quadratic equations and the elementary arithmetic of binomials and trinomials. This approach, which involved solving equations using radicals and related algebraic calculations, influenced mathematical thinking long after his death. | |||
| ], ], and ] mathematics all played an important role in the development of early Islamic mathematics. The works of mathematicians such as ], ], ], ], ] and ] were all acquired by the Islamic world and incorporated into their mathematics. Perhaps the most influential mathematical contribution from ] was the decimal ] ], also known as the ].<ref name="Berggren Islamic mathematics">{{cite book | |||
| | first=J. Lennart | |||
| | last=Berggren | |||
| | authorlink=J. Lennart Berggren | |||
| | title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook | |||
| | chapter=Mathematics in Medieval Islam | |||
| | publisher=Princeton University Press | |||
| | year=2007 | |||
| | pages=516 | |||
| | isbn=9780691114859 | |||
| | quote=The mathematics, to speak only of the subject of interest here, came principally from three traditions. The first was Greek mathematics, from the great geometrical classics of Euclid, Apollonius, and Archimedes, through the numerical solutions of indeterminate problems in Diophantus's ''Arithmatica'', to the practical manuals of Heron. But, as Bishop Severus Sebokht pointed out in the mid-seventh century, "there are also others who know something." Sebokht was referring to the Hindus, with their in genius arithmetic system based on only nine signs and a dot for an empty place. But they also contributed algebraic methods, a nascent trigonometry, and methods from solid geometry to solve problems in astronomy. The third tradition was what one may call the mathematics of practitioners. Their numbers included surveyors, builders, artisans, in geometric design, tax and treasury officials, and some merchants. Part of an oral tradition, this mathematics transcended ethnic divisions and was common heritage of many of the lands incorporated into the Islamic world. | |||
| }}</ref> The ] historian ] (c. 1050) in his book ''Tariq al-Hind'' states that the ] ] ] had an embassy in India from which was brought a book to Baghdad that was translated into Arabic as ''Sindhind''. It is generally assumed that ''Sindhind'' is none other than Brahmagupta's '']''.<ref name="Boyer Siddhanta">{{cite book|last=Boyer|authorlink=Carl Benjamin Boyer|title=|year=1991|chapter=The Arabic Hegemony|pages=226|quote=By 766 we learn that an astronomical-mathematical work, known to the Arabs as the ''Sindhind'', was brought to Baghdad from India. It is generally thought that this was the ''Brahmasphuta Siddhanta'', although it may have been the ''Surya Siddhanata''. A few years later, perhaps about 775, this ''Siddhanata'' was translated into Arabic, and it was not long afterwards (ca. 780) that Ptolemy's astrological ''Tetrabiblos'' was translated into Arabic from the Greek.}}</ref> The earliest translations from Sanskrit inspired several astronomical and astrological Arabic works, now mostly lost, some of which were even composed in verse.<ref name="Plofker 434"/> | |||
| Al-Khwārizmī's proof of the rule for solving ] of the form (ax^2 + bx = c), commonly referred to as "squares plus roots equal numbers," was a monumental achievement in the history of algebra. This breakthrough laid the groundwork for the systematic approach to solving quadratic equations, which became a fundamental aspect of algebra as it developed in the Western world.<ref name="Swetz-2012">{{Cite report |url=http://dx.doi.org/10.4169/loci003901 |title=Mathematical Treasures: Mesopotamian Accounting Tokens |last=Swetz |first=Frank J. |date=2012-08-15 |publisher=The MAA Mathematical Sciences Digital Library |location=Washington, DC}}</ref> Al-Khwārizmī's method, which involved completing the square, not only provided a practical solution for equations of this type but also introduced an abstract and generalized approach to mathematical problems. His work, encapsulated in his seminal text "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala" (The Compendious Book on Calculation by Completion and Balancing), was translated into ] in the 12th century. This translation played a pivotal role in the transmission of algebraic knowledge to Europe, significantly influencing mathematicians during the Renaissance and shaping the evolution of modern mathematics.<ref name="Swetz-2012" /> Al-Khwārizmī's contributions, especially his proof for quadratic equations, are a testament to the rich mathematical heritage of the Islamic world and its enduring impact on Western mathematics. | |||
| But Indian influences were soon overwhelmed by Greek mathematical and astronomical texts. It is not clear why this occurred but it may have been due to the greater availability of Greek texts in the region, the larger number of practitioners of Greek mathematics in the region, or because Islamic mathematicians favored the deductive exposition of the Greeks over the elliptic Sanskrit verse of the Indians. Regardless of the reason, Indian mathematics soon became mostly eclipsed by or merged with the "Graeco-Islamic" science founded on Hellenistic treatises.<ref name="Plofker 434">{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 434 | title = | quote = The early translations from Sanskrit inspired several other astronomical/astrological works in Arabic; some even imitated the Sanskrit practice of composing technical treatises in verse. Unfortunately, the earliest texts in this genre have now mostly been lost, and are known only from scattered fragments and allusions in later works. They reveal that the emergent Arabic astronomy adopted many Indian parameters, cosmological models, and computational techniques, including the use of sines.<BR>These Indian influences were soon overwhelmed - although it is not completely clear why - by those of the Greek mathematical and astronomical texts that were translated into Arabic under the Abbasid caliphs. Perhaps the greater availability of Greek works in the region, and of practitioners who understood them, favored the adoption of the Greek tradition. Perhaps its prosaic and deductive expositions seemed easier for foreign readers to grasp than elliptic Sanskrit verse. Whatever the reasons, Sanskrit inspired astronomy was soon mostly eclipsed by or merged with the "Graeco-Islamic" science founded on Hellenistic treatises.}}</ref> | |||
| The spread of Arabic mathematics to the West was facilitated by several factors. The practicality and general applicability of al-Khwārizmī's methods were significant. They were designed to convert numerical or geometrical problems into equations in normal form, leading to canonical solution formulae. His work and that of his successors like ] laid the foundation for advances in various mathematical fields, including ], ], and ].<ref>{{Cite web |title=Extending al-Karaji's Work on Sums of Odd Powers of Integers - Introduction {{!}} Mathematical Association of America |url=https://maa.org/press/periodicals/convergence/extending-al-karajis-work-on-sums-of-odd-powers-of-integers-introduction |access-date=2023-12-15 |website=maa.org |language=en}}</ref> | |||
| == Biographies == | |||
| ;{{transl|ar|ALA|]}} (786 – 833) | |||
| :Al-Ḥajjāj translated ]'s '']'' into Arabic. | |||
| ;{{transl|ar|ALA|]}} (c. 780 ]/] – c. 850 Baghdad) <!-- JPH MT AMFB --> | |||
| :Al-Khwārizmī was a ], ], ] and ]. He worked most of his life as a ] in the ] in ]. His ''Algebra'' was the first book on the systematic solution of ] and ]s. ] translations of his ''Arithmetic'', on the ], introduced the ] ] to the ] in the 12th century. He revised and updated ]'s ''Geography'' as well as writing several works on astronomy and astrology. | |||
| ;{{transl|ar|ALA|]}} (c. 800 Baghdad? – c. 860 Baghdad?)<!-- MT --> | |||
| :Al-Jawharī was a mathematician who worked at the House of Wisdom in Baghdad. His most important work was his ''Commentary on ]'' which contained nearly 50 additional ]s and an attempted ] of the ]. | |||
| ;{{transl|ar|ALA|]}} (fl. 830 Baghdad) <!-- JPH --> | |||
| :Ibn Turk wrote a work on ] of which only a chapter on the solution of ] has survied. | |||
| ;{{transl|ar|ALA|]}} (c. 801 ] – 873 Baghdad) <!-- JPH MT AMFB --> | |||
| :Al-Kindī (or Alkindus) was a ] and ] who worked as the House of Wisdom in Baghdad where he wrote commentaries on many Greek works. His contributions to mathematics include many works on ] and ]. | |||
| ;] (808 ] – 873 Baghdad) <!-- MT --> | |||
| : Hunayn (or Johannitus) was a translator who worked at the House of Wisdom in Baghdad. Translated many Greek works including those by ], ], ], ], and the ]. | |||
| ;{{transl|ar|ALA|]}} (c. 800 Baghdad – 873+ Baghdad) <!-- JPH AMFB --> | |||
| :The Banū Mūsā where three brothers who worked at the House of Wisdom in Baghdad. Their most famous mathematical treatise is ''The Book of the Measurement of Plane and Spherical Figures'', which considered similar problems as ] did in his ''On the measurement of the circle'' and ''On the sphere and the cylinder''. They contributed individually as well. The eldest, {{transl|ar|ALA|]}} (c. 800) specialised in geometry and astronomy. He wrote a critical revision on ]' ''Conics'' called ''Premises of the book of conics''. {{transl|ar|ALA|]}} (c. 805) specialised in mechanics and wrote a work on ] devices called ''On mechanics''. The youngest, {{transl|ar|ALA|]}} (c. 810) specialised in geometry and wrote a work on the ] called ''The elongated circular figure''. | |||
| ;] <!-- MT --> | |||
| ;] <!-- MT --> | |||
| ;] (Syria-Iraq, 835-901) <!-- JPH MT --> | |||
| ;] (Iraq? ca. 850-900) <!-- JPH --> | |||
| ;{{transl|ar|ALA|]}} (c. 853 ] – 929 ] near ]) <!-- JPH (Syria, ca. 900) MT --> | |||
| ;] (Egypt? ca. 900) <!-- JPH MT --> | |||
| ;] (ca. 880 - 943) <!-- MT --> | |||
| ;] <!-- MT --> | |||
| ;] (Iraq, 909-946) <!-- JPH MT --> | |||
| ;] (Iraq-Iran, ca. 920-980) <!-- JPH MT --> | |||
| ;] (Iraq? 10th century?) <!-- JPH --> | |||
| ;] (Iraq, first half of 10th century) <!-- JPH --> | |||
| :The Ikhwan al-Safa' ("brethren of purity") were a (mystical?) group in the city of Basra in Irak. The group authored a series of more than 50 letters on science, philosophy and theology. The first letter is on arithmetic and number theory, the second letter on geometry. | |||
| ;] (Iraq-Iran, 10th century) <!-- JPH MT --> | |||
| ;] (Iraq-Iran, ca. 940-1000) <!-- JPH --> | |||
| ;{{transl|ar|ALA|]}} (Iraq-Iran, ca. 940-1000) <!-- JPH MT --> | |||
| ;] <!-- MT --> | |||
| ;{{transl|ar|ALA|]}} (Iraq-Iran, ca. 940-998) <!-- JPH MT --> | |||
| ;] (Iraq-Iran, ca. 940-1000) <!-- JPH --> | |||
| ;] (Iran, ca. 940-1000) <!-- JPH MT --> | |||
| ;] (Egypt, ca. 950-1010) <!-- JPH MT --> | |||
| ;] (Iraq-Iran, ca. 950-1030) <!-- JPH MT --> | |||
| ;] (Iran, ca. 960-1010) <!-- JPH --> | |||
| ;] (Iran, ca. 970-1030) <!-- JPH MT --> | |||
| ;] (Iraq-Egypt, ca. 965-1040) <!-- JPH MT --> | |||
| ;{{transl|ar|ALA|]}} (] ] in Kath, ] – ] ] in ]) <!-- JPH MT --> | |||
| ;] <!-- MT --> | |||
| ;] <!-- MT --> | |||
| ;] <!-- MT --> | |||
| ;] (Spain, ca. 1030-1090) <!-- JPH MT --> | |||
| ;] (Azarquiel, al-Zarqali) (Spain, ca. 1030-1090) <!-- JPH --> | |||
| ;] (Spain, ca. 1080) <!-- JPH --> | |||
| ;] (Iran, ca. 1050-1130) <!-- JPH MT --> | |||
| ;{{transl|ar|ALA|]}} (c. ] ] – c. ] ]) <!-- MT --> | |||
| ;{{transl|ar|ALA|]}} (Iran, ca. 1150-1215) <!-- JPH MT --> | |||
| ;] (Maghreb, ca. 1210) <!-- JPH --> | |||
| ;] (Morocco, 13th century) <!-- JPH --> | |||
| ;{{transl|ar|ALA|]}} (] ] in ], ] – ] ] in ] near ]) <!-- JPH MT --> | |||
| ;{{transl|ar|ALA|]}} (c. 1220 Spain – c. 1283 ]) <!-- MT --> | |||
| ;{{transl|ar|ALA|]}} (c. 1250 ] – c. 1310) <!-- MT --> | |||
| ;] (Spain, ca. 1250-1320) <!-- JPH --> | |||
| ;] (Maghreb, ca. 1300) <!-- JPH MT --> | |||
| ;] (Iran, ca. 1300) <!-- JPH MT --> | |||
| ;] (Syria, ca. 1350-1400) <!-- JPH MT --> | |||
| ;] (1306-1375) <!-- JPH --> | |||
| ;'''{{transl|ar|ALA|]}}''' (1364 ] – 1436 Samarkand) <!-- MT --> | |||
| ;{{transl|ar|ALA|]}} (Iran, Uzbekistan, ca. 1420) <!-- JPH MT --> | |||
| ;] (Iran, Uzbekistan, 1394-1449) <!-- JPH MT --> | |||
| ;] <!-- MT --> | |||
| ;] (Maghreb, 15th century) <!-- JPH MT --> | |||
| ;] (Iran, 20th century) | |||
| Al-Khwārizmī's algebra was an autonomous discipline with its historical perspective, eventually leading to the "arithmetization of algebra". His successors expanded on his work, adapting it to new theoretical and technical challenges and reorienting it towards a more arithmetical direction for abstract algebraic calculation. | |||
| ==Fields== | |||
| ===Algebra=== | |||
| {{see|History of algebra}} | |||
| ]''.]] | |||
| Arabic mathematics, epitomized by al-Khwārizmī's work, was crucial in shaping the mathematical landscape. Its spread to the West was driven by its practical applications, the expansion of mathematical concepts by his successors, and the translation and adaptation of these ideas into the Western context. This spread was a complex process involving economics, politics, and cultural exchange, greatly influencing Western mathematics. | |||
| There are three theories about the origins of Arabic Algebra. The first emphasizes Hindu influence, the second emphasizes Mesopotamian or Persian-Syriac influence and the third emphasizes Greek influence. Many scholars believe that it is the result of a combination of all three sources.<ref name="Boyer Three Influences on al Jabr">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=230|isbn=0471543977}} | |||
| {{quote|"Al-Khwarizmi continued: "We have said enough so far as numbers are concerned, about the six types of equations. Now, however, it is necessary that we should demonsrate geometrically the truth of the same problems which we have explained in numbers." The ring of this passage is obviously Greek rather than Babylonian or Indian. There are, therefore, three main schools of thought on the origin of Arabic algebra: one emphasizes Hindu influence, another stresses the Mesopotamian, or Syriac-Persian, tradition, and the third points to Greek inspiration. The truth is probably approached if we combine the three theories."}}</ref> | |||
| The period known as the ] (8th to 14th century) was characterized by significant advancements in various fields, including ]. Scholars in the Islamic world made substantial contributions to ], ], ], and other ]. As a result, the intellectual achievements of Islamic scholars attracted the attention of scholars in medieval Europe who sought to access this wealth of knowledge. Trade routes, such as the ], facilitated the movement of goods, ideas, and knowledge between the East and West. Cities like ], ], and ] became centers of learning and attracted scholars from different cultural backgrounds. Therefore, mathematical knowledge from the Islamic world found its way to Europe through various channels. Meanwhile, the ] connected Western Europeans with the Islamic world. While the primary purpose of the Crusades was military, there was also cultural exchange and exposure to Islamic knowledge, including mathematics. European scholars who traveled to the Holy Land and other parts of the Islamic world gained access to Arabic manuscripts and mathematical treatises. During the 14th to 17th century, the translation of Arabic mathematical texts, along with ] and ] ones, played a crucial role in shaping the intellectual landscape of the Renaissance. Figures like ], who studied in North Africa and the Middle East, helped introduce and popularize Arabic numerals and mathematical concepts in Europe. | |||
| Throughout their time in power, before the fall of Islamic civilization, the Arabs used a fully rhetorical algebra, where sometimes even the numbers were spelled out in words. The Arabs would eventually replace spelled out numbers (eg. twenty-two) with ] (eg. 22), but the Arabs never adopted or developed a syncopated or symbolic algebra.<ref name="Boyer Islamic Rhetoric Algebra Thabit">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=234|isbn=0471543977}} | |||
| {{quote|"but al-Khwarizmi's work had a serious deficiency that had to be removed before it could serve its purpose effectively in the modern world: a symbolic notation had to be developed to replace the rhetorical form. This step the Arabs never took, except for the replacement of number words by number signs. ... Thabit was the founder of a school of translators, especially from Greek and Syriac, and to him we owe an immense debt for translations into Arabic of works by Euclid, Archimedes, Apollonius, Ptolemy, and Eutocius."}}</ref> | |||
| == Concepts == | |||
| The Muslim<ref>{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=228-229|isbn=0471543977}} | |||
| ]'s "Cubic equations and intersections of conic sections" the first page of the two-chaptered manuscript kept in Tehran University]] | |||
| {{quote|"the author's preface in Arabic gave fulsome praise to Mohammed, the prophet, and to al-Mamun, "the Commander of the Faithful"."}}</ref> | |||
| Persian mathematician {{Unicode|]}} was a faculty member of the "House of Wisdom" (Bait al-hikma) in Baghdad, which was established by Al-Mamun. Al-Khwarizmi, who died around 850 A.D., wrote more than half a dozen mathematical and astronomical works; some of which were based on the Indian ''Sindhind''.<ref name="Boyer Intro Islamic Algebra">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=227|isbn=0471543977}} | |||
| {{quote|"The first century of the Muslim empire had been devoid of scientific achievement. This period (from about 650 to 750) had been, in fact, perhaps the nadir in the development of mathematics, for the Arabs had not yet achieved intellectual drive, and concern for learning in other parts of the world had faded. Had it not been for the sudden cultural awakening in Islam during the second half of the eighth century, considerably more of ancient science and mathematics would have been lost. ... It was during the caliphate of al-Mamun (809-833), however, that the Arabs fully indulged their passion for translation. The caliph is said to have had a dream in which Aristotle appeared, and as a consequence al-Mamun determined to have Arabic versions made of all the Greek works that he could lay his hands on, including Ptolemy's ''Almagest'' and a complete version of Euclid's ''Elements''. From the Byzantine Empire, with which the Arabs maintained an uneasy peace, Greek manuscripts were obtained through peace treaties. Al-Mamun established at Baghdad a "House of Wisdom" (Bait al-hikma) comparable to the ancient Museum at Alexandria. Among the faculty members was a mathematician and astronomer, Mohammed ibn-Musa al-Khwarizmi, whose name, like that of Euclid, later was to become a household word in Western Europe. The scholar, who died sometime before 850, wrote more than half a dozen astronomical and mathematical works, of which the earliest were probably based on the ''Sindhad'' derived from India."}}</ref> | |||
| One of al-Khwarizmi's most famous books is entitled ''Al-jabr wa'l muqabalah'' or '']'', and it gives an exhaustive account of solving polynomials up to the second degree.<ref>{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=228|isbn=0471543977}} | |||
| {{quote|"The Arabs in general loved a good clear argument from premise to conclusion, as well as systematic organization - respects in which neither Diophantus nor the Hindus excelled."}}</ref> | |||
| === Algebra === | |||
| ''Al-Jabr'' is divided into six chapters, each of which deals with a different type of formula. The first chapter of ''Al-Jabr'' deals with equations whose squares equal its roots (ax² = bx), the second chapter deals with squares equal to number (ax² = c), the third chapter deals with roots equal to a number (bx = c), the fourth chapter deals with squares and roots equal a number (ax² + bx = c), the fifth chapter deals with squares and number equal roots (ax² + c = bx), and the sixth and final chapter deals with roots and number equal to squares (bx + c = ax²).<ref name="Al Jabr and its chapters">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=229|isbn=0471543977 | |||
| {{further|History of algebra}} | |||
| |quote=in six short chapters, of the six types of equations made up from the three kinds of quantities: roots, squares, and numbers (that is x, x<sup>2</sup>, and numbers). Chapter I, in three short paragraphs, covers the case of squares equal to roots, expressed in modern notation as x<sup>2</sup> = 5x, x<sup>2</sup>/3 = 4x, and 5x<sup>2</sup> = 10x, giving the answers x = 5, x = 12, and x = 2 respectively. (The root x = 0 was not recognized.) Chapter II covers the case of squares equal to numbers, and Chapter III solves the cases of roots equal to numbers, again with three illustrations per chapter to cover the cases in which the coefficient of the variable term is equal to, more than, or less than one. Chapters IV, V, and VI are mor interesting, for they cover in turn the three classical cases of three-term quadratic equations: (1) squares and roots equal to numbers, (2) squares and numbers equal to roots, and (3) roots and numbers equal to squares.}}</ref> | |||
| The study of ], the name of which is derived from the ] word meaning completion or "reunion of broken parts",<ref>{{cite web |title=algebra |work=] |url=http://www.etymonline.com/index.php?term=algebra&allowed_in_frame=0}}</ref> flourished during the ]. ], a Persian scholar in the ] in ] was the founder of algebra, is along with the ] mathematician ], known as the father of algebra. In his book '']'', Al-Khwarizmi deals with ways to solve for the ] ]s of first and second-degree (linear and quadratic) ]. He introduces the method of ], and unlike Diophantus, also gives general solutions for the equations he deals with.{{sfn|Boyer|1991|p=}}<ref>{{cite book|last=Swetz |first=Frank J. |title=Learning Activities from the History of Mathematics |url=https://books.google.com/books?id=zVYMoKhU_roC&pg=PA26 |year=1993|publisher=Walch Publishing |isbn=978-0-8251-2264-4 |page=26}}</ref><ref name=Gullberg>{{cite book |last1=Gullberg |first1=Jan |author-link=Jan Gullberg |title=Mathematics: From the Birth of Numbers |url=https://archive.org/details/mathematicsfromb1997gull |url-access=registration |date=1997 |publisher=W. W. Norton |isbn=0-393-04002-X |page=}}</ref> | |||
| 'Abd al-Hamid ibn-Turk authored a manuscript entitled ''Logical Necessities in Mixed Equations'', which is very similar to al-Khwarzimi's ''Al-Jabr'' and was published at around the same time as, or even possibly earlier than, ''Al-Jabr''.<ref name="Boyer Ibn Turk">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=234|isbn=0471543977 | |||
| |quote=The ''Algebra'' of al-Khwarizmi usually is regarded as the first work on the subject, but a recent publication in Turkey raises some questions about this. A manuscript of a work by 'Abd-al-Hamid ibn-Turk, entitled "Logical Necessities in Mixed Equations," was part of a book on ''Al-jabr wa'l muqabalah'' which was evidently very much the same as that by al-Khwarizmi and was published at about the same time - possibly even earlier. The surviving chapters on "Logical Necessities" give precisely the same type of geometric demonstration as al-Khwarizmi's ''Algebra'' and in one case the same illustrative example x<sup>2</sup> + 21 = 10x. In one respect 'Abd-al-Hamad's exposition is more thorough than that of al-Khwarizmi for he gives geometric figures to prove that if the discriminant is negative, a quadratic equation has no solution. Similarities in the works of the two men and the systematic organization found in them seem to indicate that algebra in their day was not so recent a development as has usually been assumed. When textbooks with a conventional and well-ordered exposition appear simultaneously, a subject is likely to be considerably beyond the formative stage. ... Note the omission of Diophantus and Pappus, authors who evidently were not at first known in Arabia, although the Diophantine ''Arithmetica'' became familiar before the end of the tenth century.}}</ref> | |||
| The manuscript gives the exact same geometric demonstration as is found in ''Al-Jabr'', and in one case the same example as found in ''Al-Jabr'', and even goes beyond ''Al-Jabr'' by giving a geometric proof that if the determinant is negative then the quadratic equation has no solution.<ref name="Boyer Ibn Turk" /> The similarity between these two works has led some historians to conclude that Arabic algebra may have been well developed by the time of al-Khwarizmi and 'Abd al-Hamid.<ref name="Boyer Ibn Turk" /> | |||
| Al-Khwarizmi's algebra was rhetorical, which means that the equations were written out in full sentences. This was unlike the algebraic work of Diophantus, which was syncopated, meaning that some symbolism is used. The transition to symbolic algebra, where only symbols are used, can be seen in the work of ] and ].<ref>{{MacTutor|id=Al-Banna|title=al-Marrakushi ibn Al-Banna}}</ref><ref name=Gullberg/> | |||
| ] was the successor of Abu'l-Wefa and he was the first to discover the solution to equations of the form ax<sup>2n</sup> + bx<sup>n</sup> = c.<ref name="Boyer al-Karkhi ax2n">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=239|isbn=0471543977 | |||
| |quote=Abu'l Wefa was a capable algebraist as well as a trigonometer. ... His successor al-Karkhi evidently used this translation to become an Arabic disciple of Diophantus - but without Diophantine analysis! ... In particular, to al-Karkhi is attributed the first numerical solution of equations of the form ax<sup>2n</sup> + bx<sup>n</sup> = c (only equations with positive roots were considered),}}</ref> | |||
| Al-Karkhi only considered positive roots.<ref name="Boyer al-Karkhi ax2n"/> | |||
| On the work done by Al-Khwarizmi, J. J. O'Connor and ] said:<ref>{{MacTutor |class=HistTopics |id=Arabic_mathematics |title=Arabic mathematics: forgotten brilliance?}}</ref> | |||
| Omar Khayyám (c. 1050-1123) wrote a book on Algebra that went beyond ''Al-Jabr'' to include equations of the third degree.<ref name="Boyer Omar Khayyam positive roots">{{cite book|first=Carl B.|last=Boyer|authorlink=Carl Benjamin Boyer|title=A History of Mathematics|edition=Second Edition|publisher=John Wiley & Sons, Inc.|year=1991|chapter=The Arabic Hegemony|pages=241-242|isbn=0471543977}} | |||
| {{quote|Omar Khayyam (ca. 1050-1123), the "tent-maker," wrote an ''Algebra'' that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the sixteenth century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). .. For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved."}}</ref> | |||
| Omar Khayyám provided both arithmetic and geometric solutions for quadratic equations, but he only gave geometric solutions for general cubic equations since he mistakenly believed that arithmetic solutions were impossible.<ref name="Boyer Omar Khayyam positive roots" /> His method of solving cubic equations by using intersecting conics had been used by Menaechmus, Archimedes, and Alhazen, but Omar Khayyám generalized the method to cover all cubic equations with positive roots.<ref name="Boyer Omar Khayyam positive roots" /> He only considered positive roots and he did not go past the third degree.<ref name="Boyer Omar Khayyam positive roots" /> He also saw a strong relationship between Geometry and Algebra.<ref name="Boyer Omar Khayyam positive roots" /> | |||
| {{quote|"Perhaps one of the most significant advances made by Arabic mathematics began at this time with the work of al-Khwarizmi, namely the beginnings of algebra. It is important to understand just how significant this new idea was. It was a revolutionary move away from the Greek concept of mathematics which was essentially geometry. Algebra was a unifying theory which allowed ], ]s, geometrical magnitudes, etc., to all be treated as "algebraic objects". It gave mathematics a whole new development path so much broader in concept to that which had existed before, and provided a vehicle for the future development of the subject. Another important aspect of the introduction of algebraic ideas was that it allowed mathematics to be applied to itself in a way which had not happened before." | ]}} | |||
| In the 12th century, ] found algebraic and ] solutions to cubic equations and was the first to discover the ] of ].<ref name=Berggren/> | |||
| Several other mathematicians during this time period expanded on the algebra of Al-Khwarizmi. ] wrote a book of algebra accompanied with geometrical illustrations and proofs. He also enumerated all the possible solutions to some of his problems. ], ], along with ], found several solutions of the ]. Omar Khayyam found the general geometric solution of a cubic equation.{{Citation needed|date=April 2023|reason=Wasn't Scipione del Ferro the first one?}} | |||
| J. J. O'Conner and E. F. Robertson wrote in the '']'': | |||
| === Cubic equations === | |||
| {{quote|"Perhaps one of the most significant advances made by Arabic mathematics began at this time with the work of al-Khwarizmi, namely the beginnings of algebra. It is important to understand just how significant this new idea was. It was a revolutionary move away from the Greek concept of mathematics which was essentially geometry. Algebra was a unifying theory which allowed ], ]s, geometrical magnitudes, etc., to all be treated as "algebraic objects". It gave mathematics a whole new development path so much broader in concept to that which had existed before, and provided a vehicle for future development of the subject. Another important aspect of the introduction of algebraic ideas was that it allowed mathematics to be applied to itself in a way which had not happened before."}} | |||
| ] ''x''<sup>2</sup> = ''ay'', a ] with diameter ''b''/''a''<sup>2</sup>, and a vertical line through the intersection point. The solution is given by the length of the horizontal line segment from the origin to the intersection of the vertical line and the ''x''-axis.]] | |||
| {{further|Cubic equation}} | |||
| ] (c. 1038/48 in ] – 1123/24){{sfn|Struik|1987|p=96}} wrote the ''Treatise on Demonstration of Problems of Algebra'' containing the systematic solution of ], going beyond the ''Algebra'' of al-Khwārizmī.{{sfn|Boyer|1991|pp=241–242}} Khayyám obtained the solutions of these equations by finding the intersection points of two ]s. This method had been used by the Greeks,{{sfn|Struik|1987|p=97}} but they did not generalize the method to cover all equations with positive ].{{sfn|Boyer|1991|pp=241–242}} | |||
| ===Arithmetic=== | |||
| <!--needs more context | |||
| {{main|Arabic numerals}} | |||
| Khayyám differentiated between "geometric" and "arithmetic" solutions.{{sfn|Struik|1987|p=97}} Khayyám mistakenly believed{{sfn|Boyer|1991|pp=241–242}} arithmetic solutions only existed if the ] were ] and ].{{sfn|Struik|1987|p=97}} Khayyám did not concern himself with numerical calculations of the solutions.{{sfn|Struik|1987|p=97}} | |||
| {{#tag:ref|"Omar Khayyam (ca. 1050–1123), the "tent-maker," wrote an ''Algebra'' that went beyond that of al-Khwarizmi to include equations of third degree. Like his predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the sixteenth century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, "{{sfn|Boyer|1991|pp=241–242}}|group="note"}} | |||
| --> | |||
| ] (? in ] – 1213/4) developed a novel approach to the investigation of cubic equations—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, to solve the equation <math>\ x^3 + a = b x</math>, with ''a'' and ''b'' positive, he would note that the maximum point of the curve <math>\ y = b x - x^3</math> occurs at <math>x = \textstyle\sqrt{\frac{b}{3}}</math>, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than ''a''. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.<ref>{{cite journal |last1=Berggren |first1=J. Lennart |title=Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's ''al-Muʿādalāt'' |jstor=604533 |journal=Journal of the American Oriental Society |volume=110 |issue=2 |year=1990 |pages=304–309 |doi=10.2307/604533 |last2=Al-Tūsī |first2=Sharaf Al-Dīn |last3=Rashed |first3=Roshdi}}</ref> | |||
| The ] system came to be known to both the ] mathematician ], whose book ''On the Calculation with Hindu Numerals'' written ''circa'' ], and the ] mathematician ], who wrote four volumes, ''On the Use of the Indian Numerals'' (Ketab fi Isti'mal al-'Adad al-Hindi) ''circa'' ], are principally responsible for the diffusion of the Indian system of numeration in the ] and the West . In the ], ]ern mathematicians extended the decimal numeral system to include ] using ] notation, as recorded in a treatise by ] mathematician ] in ]-]. | |||
| {{Islamic studies sidebar}} | |||
| === Induction === | |||
| In the ]—until modern times—the Arabic numeral system was used only by mathematicians. Muslim scientists used the ], and merchants used the ]. A distinctive "West Arabic" variant of the symbols begins to emerge in ca. the ] in the ] and ], called the ''ghubar'' ("sand-table" or "dust-table") numerals. | |||
| {{See also|Mathematical induction#History}} | |||
| The earliest implicit traces of mathematical induction can be found in ]'s ] (c. 300 BCE). The first explicit formulation of the principle of induction was given by ] in his {{Lang|fr|Traité du triangle arithmétique}} (1665). | |||
| The first mentions of the numerals in the West are found in the '']'' of ] . From the ], ] (later, Pope ]) began to spread knowledge of the numerals in Europe. Gerbert studied in ] in his youth, and he is known to have requested mathematical treatises concerning the ] from ] after he had returned to France. | |||
| In between, implicit ] by induction for ] was introduced by ] (c. 1000) and continued by ], who used it for special cases of the ] and properties of ]. | |||
| ], the ] scientist, wrote in ] a treatise ''On the Calculation with Hindu Numerals'', which was translated into ], as ''Algoritmi de numero Indorum'', where "Algoritmi", the translator's rendition of the author's name gave rise to the word ] (Latin ''algorithmus'') with a meaning "calculation method". blah blah blah phbbbbbbbbt whatever | |||
| === |
=== Irrational numbers === | ||
| The Greeks had discovered ]s, but were not happy with them and only able to cope by drawing a distinction between ''magnitude'' and ''number''. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including ] and ] slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations.<ref name=Sesiano/><ref>{{MacTutor|id=Al-Baghdadi|title=Abu Mansur ibn Tahir Al-Baghdadi}}</ref> They worked freely with irrationals as mathematical objects, but they did not examine closely their nature.<ref>{{cite web |last1=Allen |first1=G. Donald |date=n.d. |title=The History of Infinity |publisher=Texas A&M University |url=http://www.math.tamu.edu/~dallen/history/infinity.pdf |access-date=7 September 2016}}</ref> | |||
| Around ] AD, ], using ], found a ] for the sum of ] ].<ref>Victor J. Katz (1998). ''History of Mathematics: An Introduction'', p. 255-259. ]. ISBN 0321016181.</ref> The ] of mathematics, F. Woepcke,<ref>F. Woepcke (1853). ''Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi''. ].</ref> praised Al-Karaji for being "the first who introduced the ] of ]ic ]." Shortly afterwards, ] (known as Alhazen in the West), an ]i mathematician working in ], was the first mathematician to derive the formula for the sum of the ] ]. In turn, he developed a method for determining the general formula for the sum of any ] powers, which was fundamental to the development of ].<ref name=Katz>Victor J. Katz (1995). "Ideas of Calculus in Islam and India", ''Mathematics Magazine'' '''68''' (3), p. 163-174.</ref> | |||
| In the twelfth century, ] translations of ]'s ] on the ] introduced the ] ] to the ].<ref name="Struik 93">{{harvnb|Struik|1987| p= 93}}</ref> His ''Compendious Book on Calculation by Completion and Balancing'' presented the first systematic solution of ] and ]s. In ] Europe, he was considered the original inventor of algebra, although it is now known that his work is based on older Indian or Greek sources.{{sfn|Rosen|1831|p=v–vi}}<ref>{{cite encyclopedia |last=Toomer |first=Gerald |author-link=Gerald Toomer |title=Al-Khwārizmī, Abu Ja'far Muḥammad ibn Mūsā |encyclopedia=] |volume=7 |editor=Gillispie, Charles Coulston |publisher=Charles Scribner's Sons |location=New York |date=1990 |isbn=0-684-16962-2 |url=http://www.encyclopedia.com/doc/1G2-2830902300.html |via=Encyclopedia.com}}</ref> He revised ]'s '']'' and wrote on astronomy and astrology. However, ] suggests that al-Khwarizmi's original work was not based on Ptolemy but on a derivative world map,{{sfn|Nallino|1939}} presumably in ] or ]. | |||
| === Spherical trigonometry === | |||
| The ] ] mathematician ] saw a strong relationship between geometry and algebra, and was moving in the right direction when he helped to close the gap between numerical and geometric algebra<ref name="Boyer Omar Khayyam positive roots"/> with his geometric solution of the general ]s,<ref>Glen M. Cooper (2003). "Omar Khayyam, the Mathmetician", ''The Journal of the American Oriental Society'' '''123'''.</ref> but the decisive step in ] came later with Descartes.<ref name="Boyer Omar Khayyam positive roots">{{cite book|last=Boyer|authorlink=Carl Benjamin Boyer|title=|year=1991|chapter=The Arabic Hegemony|pages=241-242|quote=Omar Khayyam (ca. 1050-1123), the "tent-maker," wrote an ''Algebra'' that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the sixteenth century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). .. For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved."}}</ref> In the 12th century, the ] mathematician ] was the first to discover the ] of ], an important result in ].<ref name=Berggren>J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", ''Journal of the American Oriental Society'' '''110''' (2), p. 304-309.</ref> | |||
| {{further|Law of sines|History of trigonometry}} | |||
| The spherical ] was discovered in the 10th century: it has been attributed variously to ], ] and ], with ] as a contributor.<ref name=Sesiano>{{cite book | |||
| ===Cryptography=== | |||
| | last = Sesiano | first = Jacques | |||
| In the 9th century, ] was a pioneer in ] and ]. He gave the first known recorded explanation of ] in ''A Manuscript on Deciphering Cryptographic Messages''. In particular, he is credited with developing the ] method whereby variations in the frequency of the occurrence of letters could be analyzed and exploited to break ] (i.e. crypanalysis by frequency analysis).<ref>Simon Singh. The Code Book. p. 14-20</ref> This was detailed in a text recently rediscovered in the Ottoman archives in Istanbul, ''A Manuscript on Deciphering Cryptographic Messages'', which also covers methods of cryptanalysis, encipherments, cryptanalysis of certain encipherments, and statistical analysis of letters and letter combinations in Arabic.<ref>{{cite web |url=http://www.muslimheritage.com/topics/default.cfm?ArticleID=372 |title= Al-Kindi, Cryptgraphy, Codebreaking and Ciphers |accessdate=2007-01-12 |format= HTML |work= }}</ref> | |||
| | editor-last = Selin | editor-first = Helaine | editor-link = Helaine Selin | |||
| | contribution = Islamic Mathematics | |||
| | doi = 10.1007/978-94-011-4301-1_9 | |||
| | isbn = 978-94-011-4301-1 | |||
| | pages = 137–165 | |||
| | publisher = Springer Netherlands | |||
| | title = Mathematics Across Cultures: The History of Non-Western Mathematics | |||
| | year = 2000}}</ref> ]'s ''The book of unknown arcs of a sphere'' in the 11th century introduced the general law of sines.<ref name="MacTutor Al-Jayyani">{{MacTutor |id=Al-Jayyani |title=Abu Abd Allah Muhammad ibn Muadh Al-Jayyani}}</ref> The plane law of sines was described in the 13th century by ]. In his ''On the Sector Figure'', he stated the law of sines for plane and spherical triangles and provided proofs for this law.{{sfn|Berggren|2007|p=518}} | |||
| === Negative numbers === | |||
| ] (1355-1418) wrote the ''Subh al-a 'sha'', a 14-volume encyclopedia which included a section on cryptology. This information was attributed to Taj ad-Din Ali ibn ad-Duraihim ben Muhammad ath-Tha 'alibi al-Mausili who lived from 1312 to 1361, but whose writings on cryptology have been lost. The list of ciphers in this work included both ] and ], and for the first time, a cipher with multiple substitutions for each ] letter. Also traced to Ibn al-Duraihim is an exposition on and worked example of cryptanalysis, including the use of tables of ] and sets of letters which can not occur together in one word. | |||
| {{further|Negative numbers}} | |||
| In the 9th century, Islamic mathematicians were familiar with negative numbers from the works of Indian mathematicians, but the recognition and use of negative numbers during this period remained timid.<ref name=Rashed>{{Cite book| publisher = Springer| isbn = 9780792325659| last = Rashed| first = R.| title = The Development of Arabic Mathematics: Between Arithmetic and Algebra| date =1994-06-30|pages=36–37}}</ref> ] did not use negative numbers or negative coefficients.<ref name=Rashed /> But within fifty years, ] illustrated the rules of signs for expanding the multiplication <math>(a \pm b)(c \pm d)</math>.<ref name=Ismail>{{citation | author = Mat Rofa Bin Ismail | title = Algebra in Islamic Mathematics | encyclopedia = Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures | volume = 1 | year = 2008 | publisher = Springer | isbn = 9781402045592 | editor = Helaine Selin | editor-link = Helaine Selin | page=115 | edition=2nd}}</ref> ] wrote in his book ''al-Fakhrī'' that "negative quantities must be counted as terms".<ref name=Rashed /> In the 10th century, ] considered debts as negative numbers in ''A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen''.<ref name=Ismail /> | |||
| By the 12th century, al-Karaji's successors were to state the general rules of signs and use them to solve ]s.<ref name=Rashed /> As ] writes: | |||
| <blockquote>the product of a negative number—''al-nāqiṣ''—by a positive number—''al-zāʾid''—is negative, and by a negative number is positive. If we subtract a negative number from a higher negative number, the remainder is their negative difference. The difference remains positive if we subtract a negative number from a lower negative number. If we subtract a negative number from a positive number, the remainder is their positive sum. If we subtract a positive number from an empty power (''martaba khāliyya''), the remainder is the same negative, and if we subtract a negative number from an empty power, the remainder is the same positive number.<ref name=Rashed /></blockquote> | |||
| === |
=== Double false position === | ||
| {{further|False position method}} | |||
| {{see|History of geometry}} | |||
| ] featuring ], from the title page of the ''De scientia motus orbis'' (Latin version with engraving, 1504). As in many medieval illustrations, the ] here is an icon of religion as well as science, in reference to God as the architect of creation]] | |||
| Between the 9th and 10th centuries, the ] mathematician ] wrote a now-lost treatise on the use of double false position, known as the ''Book of the Two Errors'' (''Kitāb al-khaṭāʾayn''). The oldest surviving writing on double false position from the ] is that of ] (10th century), an ] mathematician from ], ]. He justified the technique by a formal, ]. Within the tradition of Golden Age Muslim mathematics, double false position was known as ''hisāb al-khaṭāʾayn'' ("reckoning by two errors"). It was used for centuries to solve practical problems such as commercial and juridical questions (estate partitions according to rules of ]), as well as purely recreational problems. The algorithm was often memorized with the aid of ], such as a verse attributed to ] and balance-scale diagrams explained by ] and ], who were each mathematicians of ] origin.<ref>{{Cite conference |conference=Eighth North African Meeting on the History of Arab Mathematics |last=Schwartz |first=R. K. |title=Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position) |location=Radès, Tunisia |year=2004 |url=http://www.ub.edu/islamsci/Schwartz.pdf |access-date=2012-06-08 |archive-url=https://web.archive.org/web/20140516012137/http://www.ub.edu/islamsci/Schwartz.pdf |archive-date=2014-05-16}} {{cite web|url=http://facstaff.uindy.edu/~oaks/Biblio/COMHISMA8paper.doc |title=Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position) |archive-url=https://web.archive.org/web/20110915195359/http://facstaff.uindy.edu/%7Eoaks/Biblio/COMHISMA8paper.doc |archive-date=2011-09-15 |url-status=dead |format=.doc}}</ref> | |||
| The successors of ] (born ]) undertook a systematic application of arithmetic to algebra, algebra to arithmetic, both to trigonometry, algebra to the ]ean theory of numbers, algebra to geometry, and geometry to algebra. This was how the creation of polynomial algebra, combinatorial analysis, numerical analysis, the numerical solution of equations, the new elementary theory of numbers, and the geometric construction of equations arose. | |||
| == Influences == | |||
| ] (born ]) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. ] (born ]) completely freed algebra from geometrical operations and replaced them with the ]al type of operations which are at the core of algebra today. | |||
| The influence of medieval Arab-Islamic mathematics to the rest of the world is wide and profound, in both the realm of science and mathematics. The knowledge of the Arabs went into the western world through ] and ] during the translation movement. "The Moors (western Mohammedans from that part of North Africa once known as Mauritania) crossed over into Spain early in the seventh century, bringing with them the cultural resources of the Arab world".<ref name="Masters-2011a">{{Cite journal |last=Masters |first=Barry R. |date=2011-06-08 |title=Biomedical ethics, 7th edition David DeGrazia, Thomas A. Mappes, Jeffrey Brand-Ballard: 2010, Softcover, 732pp, ISBN-9780073407456 £171.15 McGraw-Hill Incorporated |url=http://dx.doi.org/10.1007/s00417-011-1640-x |journal=Graefe's Archive for Clinical and Experimental Ophthalmology |volume=250 |issue=1 |pages=159–160 |doi=10.1007/s00417-011-1640-x |issn=0721-832X}}</ref> In the 13th century, King ] established the ], in the ], where scholars translated numerous scientific and philosophical works from ] into ]. The translations included Islamic contributions to ], which helps European mathematicians and astronomers in their studies. European scholars such as ] (1114–1187) played a key role in translating and disseminating these works, thus making them accessible to a wider audience. Cremona is said to have translated into Latin "no fewer than 90 complete Arabic texts."<ref name="Masters-2011a" /> European mathematicians, building on the foundations laid by Islamic scholars, further developed practical trigonometry for applications in navigation, cartography, and celestial navigation, thus pushing forward the age of discovery and scientific revolution. The practical applications of trigonometry for navigation and astronomy became increasingly important during the Age of Exploration. | |||
| ] is one of the islamic mathematicians who made great contributions to the development of trigonometry. He "innovated new trigonometric functions, created a table of cotangents, and made some formulas in spherical trigonometry."<ref>{{Citation |title=Edited by |date=1972 |url=http://dx.doi.org/10.1016/s0049-237x(08)71546-5 |work=Contributions to Non-Standard Analysis |pages=iii |access-date=2023-12-15 |publisher=Elsevier}}</ref> These discoveries, together with his astronomical works which are praised for their accuracy, greatly advanced astronomical calculations and instruments. | |||
| Although ] (known as Thebit in ]) (born ]) contributed to a number of areas in mathematics, where he played an important role in preparing the way for such important mathematical discoveries as the extension of the concept of number to (]) ]s, ], theorems in ], ], and ]. An important geometrical aspect of Thabit's work was his book on the composition of ratios. In this book, Thabit deals with arithmetical operations applied to ratios of geometrical quantities. The Greeks had dealt with geometric quantities but had not thought of them in the same way as numbers to which the usual rules of arithmetic could be applied. By introducing arithmetical operations on quantities previously regarded as geometric and non-numerical, Thabit started a trend which led eventually to the generalization of the number concept. Another important contribution Thabit made to ] was his generalization of the ], which he extended from ] to all ]s in general, along with a general ].<ref>Aydin Sayili (1960). "Thabit ibn Qurra's Generalization of the Pythagorean Theorem", '']'' '''51''' (1), p. 35-37.</ref> | |||
| ] (1048–1131) was a Persian mathematician, astronomer, and poet, known for his work on algebra and geometry, particularly his investigations into the solutions of cubic equations. He was "the first in history to elaborate a geometrical theory of equations with degrees ≤ 3",<ref name="Rashed-2014">{{Cite book |last=Rashed |first=Roshdi |url=http://dx.doi.org/10.4324/9781315753867 |title=Classical Mathematics from Al-Khwarizmi to Descartes |date=2014-08-21 |publisher=Routledge |isbn=978-1-317-62239-0}}</ref> and has great influence on the work of Descartes, a French mathematician who is often regarded as the founder of analytical geometry. Indeed, "to read ]' Géométrie is to look upstream towards al-Khayyām and al-Ṭūsī; and downstream towards Newton, Leibniz, Cramer, Bézout and the Bernoulli brothers".<ref name="Rashed-2014" /> Numerous problems that appear in "La Géométrie" (Geometry) have foundations that date back to al-Khayyām. | |||
| ] (born ]), who introduced a method of ] more general than that of ], and ] (born ]) were leading figures in a revival and continuation of Greek higher geometry in the Islamic world. These mathematicians, and in particular ], studied ] and investigated the optical properties of mirrors made from ]s. | |||
| ] ({{Langx|ar|أبو كامل شجاع بن أسلم بن محمد بن شجاع|links=no}}, also known as Al-ḥāsib al-miṣrī—lit. "The Egyptian Calculator") (c. 850 – c. 930), was studied algebra following the author of ''Algebra'', al-Khwārizmī. His ''Book of Algebra'' (Kitāb fī al-jabr wa al-muqābala) is "essentially a commentary on and elaboration of al-Khwārizmī's work; in part for that reason and in part for its own merit, the book enjoyed widespread popularity in the Muslim world".<ref name="Masters-2011b">{{Cite journal |last=Masters |first=Barry R. |date=2011-06-08 |title=Biomedical ethics, 7th edition David DeGrazia, Thomas A. Mappes, Jeffrey Brand-Ballard: 2010, Softcover, 732pp, ISBN-9780073407456 £171.15 McGraw-Hill Incorporated |url=http://dx.doi.org/10.1007/s00417-011-1640-x |journal=Graefe's Archive for Clinical and Experimental Ophthalmology |volume=250 |issue=1 |pages=159–160 |doi=10.1007/s00417-011-1640-x |issn=0721-832X}}</ref> It contains 69 problems, which is more than al-Khwārizmī who had 40 in his book.<ref name="Masters-2011b" /> Abū Kāmil's Algebra plays a significant role in shaping the trajectory of Western mathematics, particularly in its impact on the works of the Italian mathematician Leonardo of Pisa, widely recognized as Fibonacci. In his ''Liber Abaci'' (1202), Fibonacci extensively incorporated ideas from Arabic mathematicians, using approximately 29 problems from ''Book of Algebra'' with scarce modification.<ref name="Masters-2011b" /> | |||
| Astronomy, time-keeping and ] provided other motivations for geometrical and trigonometrical research. For example Ibrahim ibn Sinan and his grandfather ] both studied curves required in the construction of sundials. ] and ] both applied ] to astronomy. | |||
| == Western historians' perception of the contribution of Arab mathematicians == | |||
| ] (born ]) was a ] mathematician, as well as a poet. Along with his fame as a poet, he was also famous during his lifetime as a mathematician, well known for inventing the general method of solving ]s by intersecting a parabola with a circle. In addition he discovered the ], and authored criticisms of ]'s theories of ] which made their way to England, where they contributed to the eventual development of ]. Omar Khayyam also combined the use of trigonometry and ] to provide methods of solving algebraic equations by geometrical means. His work marked the beginnings of ]<ref>R. Rashed (1994). ''The development of Arabic mathematics: between arithmetic and algebra''. ].</ref><ref>{{MacTutor|class=HistTopics|id=Arabic_mathematics|title=Arabic mathematics: forgotten brilliance?|year=1999}}</ref> and ].<ref name=Cooper/> Khayyam also made the first attempt at formulating a ] ] as an alternative to the ] ],<ref>Victor J. Katz (1998), ''History of Mathematics: An Introduction'', p. 270, ], ISBN 0321016181: {{quote|"In some sense, his treatment was better than ibn al-Haytham's because he explicitly formulated a new postulate to replace Euclid's rather than have the latter hidden in a new definition."}}</ref> and he was the first to consider the cases of ] and ], though he excluded the latter.<ref name=Rosenfeld>Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., '']'', Vol. 2, p. 447-494 , ], London and New York: {{quote|"Khayyam's postulate had excluded the case of the hyperbolic geometry whereas al-Tusi's postulate ruled out both the hyperbolic and elliptic geometries."}}</ref> | |||
| Despite the fundamental works Arabic mathematicians have done on the development of Algebra and algebraic geometry, Western historians in the 18th and early 19th century still regarded it as a fact that ] and math were unique phenomena of the West. Even though some math contributions from Arab mathematicians are occasionally acknowledged, they are considered to be "outside history or only integrated in so far as it contributed to science, which is essentially European",<ref name="Rashed-1994">{{Cite journal |last=Rashed |first=Roshdi |date=1994 |title=The Development of Arabic Mathematics: Between Arithmetic and Algebra |url=http://dx.doi.org/10.1007/978-94-017-3274-1 |journal=Boston Studies in the Philosophy of Science |doi=10.1007/978-94-017-3274-1 |issn=0068-0346}}</ref> and just some technical innovations to the ] heritage rather than open up a completely new branch of mathematics. In the French philosopher ]'s work, Arabic math is merely "a reflection of ], combined with ] and Indian influences". And according to ], "Arabic science only reproduced the teachings received from Greek science". Besides being considered as merely some insignificant additions or reflections to the great tradition of Greek classical science, math works from Arabic mathematicians are also blamed for lacking rigor and too focused on practical applications and calculations, and this is why Western historians argued they could never reach the level of Greek mathematicians.<ref name="Rashed-1994" /> As ] wrote, Arabic math "in no way superseded the level attained by Diophantus". On the other hand, they perceived that Western mathematicians went into a very different way both in its method employed and ultimate purpose, "the hallmark of Western science in its Greek origins as well as in its modern renaissance, is its conformity to rigorous standards".<ref name="Rashed-1994" /> Thus, the perceived non-rigorous proof in Arabic mathematicians' book authorizes ] to exclude the Arabic period when he retraced the evolution of algebra.<ref name="Rashed-1994" /> And instead, the history of classical algebra is written as the work of the ] and the origin of algebraic geometry is traced back to Descartes, while Arabic mathematicians' contributions are ignored deliberately. In Rashed's words: "To justify the exclusion of science written in Arabic from the history of science, one invokes its absence of rigor, its calculatory appearance and its practical aims. Furthermore, strictly dependent on Greek science and, lastly, incapable of introducing experimental norms, scientists of that time were relegated to the role of conscientious guardians of the Hellenistic museum."<ref name="Rashed-1994" /> | |||
| In 18th century ] and ], the prevailing ] view was "East and West oppose each other not as geographical but as historical positivities",<ref name="Rashed-1994" /> which labeled "]" as the essence of the West, while the "Call of the ]" movement emerged in the 19th century was interpreted as "against Rationalism"<ref name="Rashed-1994" /> and a return to a more "spiritual and harmonious" lifestyle. Thus, the prevailing ] in that period was one of the main reasons why Arabic mathematicians were often ignored for their contributions, as people outside the West were considered to be lacking the necessary rationality and scientific spirit to made significant contributions to math and science. | |||
| Persian mathematician ] (born ]) did not follow the general development that came through ]'s school of algebra but rather followed Khayyam's application of algebra to geometry. He wrote a treatise on cubic equations, which represents an essential contribution to another algebra which aimed to study curves by means of equations, thus inaugurating the study of algebraic geometry. | |||
| == Conclusion == | |||
| In 1250, ], in his ''Al-risala al-shafiya'an al-shakk fi'l-khutut al-mutawaziya'' (''Discussion Which Removes Doubt about Parallel Lines''), wrote detailed critiques of the ] ] and on ]'s attempted proof a century earlier. Nasir al-Din attempted to derive a ] of the parallel postulate.<ref name=Katz/> He was one of the first to consider the cases of ] and ], though he ruled out both of them.<ref name=Rosenfeld/> | |||
| The medieval Arab-Islamic world played a crucial role in shaping the trajectory of mathematics, with ]'s algebraic innovations serving as a cornerstone. The dissemination of Arabic mathematics to the West during the ], facilitated by cultural exchanges and translations, left a lasting impact on Western mathematical thought. Mathematicians like ], ], and ], with their contributions to ], ], and ], extended their influence beyond their time. Despite the foundational contributions of Arab mathematicians, Western historians in the 18th and early 19th centuries, influenced by ] views, sometimes marginalized these achievements. The East lacking rationality and scientific spirit perpetuated a biased perspective, hindering the recognition of the significant role played by Arabic mathematics in the development of algebra and other mathematical disciplines. Reevaluating the history of mathematics necessitates acknowledging the interconnectedness of diverse mathematical traditions and dispelling the notion of a uniquely European mathematical heritage. The contributions of Arab mathematicians, marked by practical applications and theoretical innovations, form an integral part of the rich tapestry of mathematical history, and deserves recognition. | |||
| == Other major figures == | |||
| His son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), wrote a book on the subject in 1298, based on al-Tusi's later thoughts, which presented one of the earliest arguments for a ] hypothesis equivalent to the parallel postulate.<ref name=Katz/><ref>Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., '']'', Vol. 2, p. 447-494 , ], London and New York: {{quote|"In ''Pseudo-Tusi's Exposition of Euclid'', another statement is used instead of a postulate. It was independant of the Euclidean postulate V and easy to prove. He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the ''Elements''."}}</ref> Sadr al-Din's work was published in ] in 1594 and was studied by European geometers. This work marked the starting point for ]'s work on the subject, and eventually the development of modern ].<ref name=Katz>Victor J. Katz (1998), ''History of Mathematics: An Introduction'', p. 270-271, ], ISBN 0321016181: <blockquote>"But in a manuscript probably written by his son Sadr al-Din in 1298, based on Nasir al-Din's later thoughts on the subject, there is a new argument based on another hypothesis, also equivalent to Euclid's, The importance of this latter work is that it was published in Rome in 1594 and was studied by European geometers. In particular, it became the starting point for the work of Saccheri and ultimately for the discovery of non-Euclidean geometry."<blockquote></ref> A proof from Sadr al-Din's work was quoted by ] and Saccheri in the 17th and 18th centuries. They both derived their proofs of the parallel postulate from Sadr al-Din's work, while Saccheri also derived his ] from Sadr al-Din, who himself based it on his father's work.<ref>Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., '']'', Vol. 2, p. 447-494 , ], London and New York: {{quote|"His book published in Rome considerably influenced the subsequent development of the theory of parallel lines. Indeed, J. Wallis (1616-1703) included a Latin translation of the proof of postulate V from this book in his own writing ''On the Fifth Postulate and the Fifth Definition from Euclid's Book 6'' (''De Postulato Quinto et Definitione Quinta lib. 6 Euclidis'', 1663). Saccheri quited this proof in his ''Euclid Cleared of all Stains'' (''Euclides ab omni naevo vindicatus'', 1733). It seems possible that he borrowed the idea of considering the three hypotheses about the upper angles of the 'Saccheri quadrangle' from Pseudo-Tusi. The latter inserted the exposition of this subject into his work, taking it from the writings of al-Tusi and Khayyam."}}</ref> | |||
| * ] (fl. 830) (quadratics) | |||
| * ] (d. after 864) | |||
| * ] (826–901) | |||
| * ] (before 858 – 929) | |||
| * ] (c. 850 – c. 930) | |||
| * ] (fl. 952) (arithmetic) | |||
| * ] (d. 967) | |||
| * ] (c. 940–1000) (centres of gravity) | |||
| * ] (c. 965–1040) | |||
| * ] (973–1048) (trigonometry) | |||
| * ] (1048–1131) | |||
| * ] (c. 1116–1196) | |||
| * ] (1136–1206) | |||
| * ] (c. 1380–1429) (decimals and estimation of the circle constant) | |||
| == Gallery == | |||
| The theorems of ] (Alhacen), ] and ] on ]s, including the ] and ], were the first theorems on ] and ], and along with their alternative postulates, such as ], these works marked the beginning of ] and had a considerable influence on its development among later European geometers, including ], ], ], ], and ].<ref>Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., '']'', Vol. 2, p. 447-494 , ], London and New York: {{quote|"Three scientists, Ibn al-Haytham, Khayyam and al-Tusi, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the ninteenth century. In essence their propositions concerning the properties of quadrangles which they considered assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between tthis postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investiagtions of their European couterparts. The first European attempt to prove the postulate on parallel lines - made by Witelo, the Polish scientists of the thirteenth century, while revising Ibn al-Haytham's '']'' (''Kitab al-Manazir'') - was undoubtedly prompted by Arabic sources. The proofs put forward in the fourteenth century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that ''Pseudo-Tusi's Exposition of Euclid'' had stimulated borth J. Wallis's and G. Saccheri's studies of the theory of parallel lines."}}</ref> | |||
| <gallery> | |||
| File:Gravure originale du compas parfait par Abū Sahl al-Qūhī.jpg|Engraving of ]'s perfect compass to draw conic sections | |||
| File:Theorem of al-Haitham.JPG|The ] | |||
| </gallery> | |||
| == See also == | |||
| ===Mathematical induction=== | |||
| * ] | |||
| The first known ] by ] was introduced in the ''al-Fakhri'' written by ] around ] AD, who used it to prove ] such as the ], ], and the sum formula for ] ].<ref>Victor J. Katz (1998), ''History of Mathematics: An Introduction'', p. 255-259, ], ISBN 0321016181: | |||
| * ] | |||
| <blockquote>"Another important idea introduced by ] and continued by ] and others was that of an inductive argument for dealing with certain arithmetic sequences. Thus al-Karaji used such an argument to prove the result on the sums of integral cubes already known to ] Al-Karaji did not, however, state a general result for arbitary ''n''. He stated his theorem for the particular integer 10 His proof, nevertheless, was clearly designed to be extendable to any other integer.</blockquote></ref><ref>{{MacTutor|id=Al-Karaji|title=Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji}} {{quote|"Al-Karaji also uses a form of mathematical induction in his arguments, although he certainly does not give a rigorous exposition of the principle."}}</ref> His proof was the first to make use of the two basic components of an inductive proof, "namely the ] of the statement for ''n'' = 1 (1 = 1<sup>3</sup>) and the deriving of the truth for ''n'' = ''k'' from that of ''n'' = ''k'' - 1."<ref>Katz (1998), p. 255: <blockquote>"Al-Karaji's argument includes in essence the two basic components of a modern argument by induction, namely the truth of the statement for ''n'' = 1 (1 = 1<sup>3</sup>) and the deriving of the truth for ''n'' = ''k'' from that of ''n'' = ''k'' - 1. Of course, this second component is not explicit since, in some sense, al-Karaji's argument is in reverse; this is, he starts from ''n'' = 10 and goes down to 1 rather than proceeding upward. Nevertheless, his argument in ''al-Fakhri'' is the earliest extant proof of the sum formula for integral cubes."</blockquote></ref> | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| == References == | |||
| Shortly afterwards, ] (Alhazen) used the inductive method to prove the sum of ]s, and by extension, the sum of any integral ], which was an important result in ] ]. He only stated it for particular integers, but his proof for those integers was by induction and generalizable.<ref>Victor J. Katz (1995), "Ideas of Calculus in Islam and India", ''Mathematics Magazine'' '''68''' (3), p. 163-174: | |||
| {{Reflist|30em}} | |||
| {{quote|"The central idea in ]'s proof of the sum formulas was the derivation of the equation Naturally, he did not state this result in general form. He only stated it for particular integers, but his proof for each of those ''k'' is by induction on ''n'' and is immediately generalizable to any value of ''k''."}}</ref><ref>Katz (1998), p. 255-259.</ref> | |||
| == Sources ==<!--should be harvard, must be used in refs above--> | |||
| ] came closest to a modern proof by mathematical induction in pre-modern times, which he used to extend the proof of the binomial theorem and Pascal's triangle previously given by al-Karaji. Al-Samaw'al's inductive argument was only a short step from the full inductive proof of the general binomial theorem.<ref>Katz (1998), p. 259: <blockquote>"Like the proofs of al-Karaji and ibn al-Haytham, al-Samaw'al's argument contains the two basic components of an inductive proof. He begins with a value for which the result is known, here ''n'' = 2, and then uses the result for a given integer to derive the result for the next. Although al-Samaw'al did not have any way of stating, and therefore proving, the general binomial theorem, to modern readers there is only a short step from al-Samaw'al's argument to a full inductive proof of the binomial theorem."</blockquote></ref> | |||
| {{refbegin|2}} | |||
| * {{cite book |last=Berggren |first=J. Lennart |editor=Victor J. Katz |year=2007 |title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook|chapter=Mathematics in Medieval Islam|edition=2nd |publisher=] |location=Princeton, New Jersey |isbn=978-0-691-11485-9}} | |||
| * {{Citation|last=Boyer|year=1991|first=Carl B.|author-link=Carl Benjamin Boyer|title=A History of Mathematics|chapter=Greek Trigonometry and Mensuration, and The Arabic Hegemony|edition=2nd|publisher=John Wiley & Sons|location=New York City|isbn=0-471-54397-7|url=https://archive.org/details/historyofmathema00boye}} | |||
| * {{cite book |last=Katz|year=1993|first=Victor J. |title=A History of Mathematics: An Introduction|publisher=HarperCollins college publishers|isbn=0-673-38039-4}} | |||
| * {{Citation |last=Nallino |first=C.A. |author-link=C.A. Nallino |contribution=Al-Ḥuwārismī e il suo rifacimento della Geografia di Tolomeo |pages=458–532 |title=Raccolta di scritti editi e inediti |volume=V |location=Rome |publisher=Istituto per l'Oriente |year=1939 |language=it}} | |||
| * {{cite book |last=Rosen|first=Fredrick |title=The Algebra of Mohammed Ben Musa|date=1831|publisher=Kessinger Publishing |isbn=1-4179-4914-7 |url=https://archive.org/details/algebraofmohamme00khuwrich}} | |||
| * {{cite book |last=Smith|year=1958|first=David E.|author-link=David Eugene Smith|title=History of Mathematics|publisher=Dover Publications|isbn=0-486-20429-4}} | |||
| * {{Citation|last=Struik|year=1987|first=Dirk J.|author-link=Dirk Jan Struik|title=A Concise History of Mathematics|edition=4th rev.|publisher=Dover Publications|isbn=0-486-60255-9|url-access=registration|url=https://archive.org/details/concisehistoryof0000stru_m6j1}} | |||
| {{refend}} | |||
| == |
==Further reading== | ||
| {{Refbegin|2}} | |||
| In ], ] solved problems involving ] using what is now called ]. In his ''Opuscula'', Ibn al-Haytham considers the solution of a system of congruences, and gives two general methods of solution. His first method, the canonical method, involved Wilson's theorem, while his second method involved a version of the ]. Another contribution to number theory is his work on ]s. In his ''Analysis and synthesis'', Ibn al-Haytham was the first to discover that every even perfect number is of the form 2<sup>''n''−1</sup>(2<sup>''n''</sup> − 1) where 2<sup>''n''</sup> − 1 is ], but he was not able to prove this result successfully (] later proved it in the 18th century).<ref>{{MacTutor Biography|id=Al-Haytham|title=Abu Ali al-Hasan ibn al-Haytham}}</ref> | |||
| ;Books on Islamic mathematics | |||
| * {{cite book |last=Berggren |first=J. Lennart |title=Episodes in the Mathematics of Medieval Islam|year=1986|publisher=Springer-Verlag|location=New York|isbn=0-387-96318-9}} | |||
| In ], ]s were known to ] mathematicians, possibly as early as the 7th century, when the Arabs got into contact with Indian or South Asian culture, and learned Indian mathematics and astronomy, including other aspects of ]. It has also been suggested that the idea came via China. The first magic squares of order 5 and 6 appear in an encyclopedia from ] ''circa'' 983 AD, the ] (the Encyclopedia of the Brethern of Purity); simpler magic squares were known to several earlier Arab mathematicians.<ref name="Swaney">Swaney, Mark. .</ref> | |||
| ** Review: {{cite journal |last1=Toomer|first1=Gerald J.|author-link=Gerald J. Toomer|title=Episodes in the Mathematics of Medieval Islam |journal=] |volume=95 |issue=6 |year=1988 |doi=10.2307/2322777 |page=567 |publisher=Mathematical Association of America|last2=Berggren|first2=J. L.|jstor=2322777}} | |||
| ** Review: {{cite journal |last1=Hogendijk |first1=Jan P.| title=''Episodes in the Mathematics of Medieval Islam'' by J. Lennart Berggren |journal=Journal of the American Oriental Society |volume=109 |issue=4 |year=1989 |pages=697–698 |doi=10.2307/604119 |publisher=American Oriental Society|last2=Berggren|first2=J. L. |jstor=604119}} | |||
| * {{cite book |last=Daffa' |first=Ali Abdullah al- |author-link=Ali Abdullah Al-Daffa |title=The Muslim contribution to mathematics |year=1977 |publisher=Croom Helm |location=London |isbn=0-85664-464-1}} | |||
| * {{cite book |last=Ronan|year=1983|first=Colin A.|author-link=Colin Ronan|title=The Cambridge Illustrated History of the World's Science|publisher=Cambridge University Press|isbn=0-521-25844-8}} | |||
| * {{cite book |last=Rashed|first=Roshdi |author-link=Roshdi Rashed |others=Translated by A. F. W. Armstrong |title=The Development of Arabic Mathematics: Between Arithmetic and Algebra |publisher=Springer|year=2001 |isbn=0-7923-2565-6}} | |||
| * {{cite book |last=Youschkevitch |first=Adolf P. |author-link=Adolph Pavlovich Yushkevich |author2=Rozenfeld, Boris A. |title=Die Mathematik der Länder des Ostens im Mittelalter |year=1960|location=Berlin}} Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160. | |||
| * {{cite book |last=Youschkevitch |first=Adolf P. |title=Les mathématiques arabes: VIII<sup>e</sup>–XV<sup>e</sup> siècles |others=translated by M. Cazenave and K. Jaouiche |publisher=Vrin |location=Paris |year=1976 |isbn=978-2-7116-0734-1}} | |||
| ; Book chapters on Islamic mathematics | |||
| The Arab mathematician ], who worked on magic squares around 1200 AD, attributed mystical properties to them, although no details of these supposed properties are known. There are also references to the use of magic squares in astrological calculations, a practice that seems to have originated with the Arabs.<ref name="Swaney"/> | |||
| * Lindberg, D.C., and M. H. Shank, eds. ''The Cambridge History of Science. Volume 2: Medieval Science'' (Cambridge UP, 2013), chapters 2 and 3 mathematics in Islam. | |||
| * {{cite book | first=Roger | last=Cooke | author-link=Roger Cooke (mathematician) | title=The History of Mathematics: A Brief Course | chapter=Islamic Mathematics | publisher=Wiley-Interscience | year=1997 | isbn=0-471-18082-3 | url=https://archive.org/details/historyofmathema0000cook }} | |||
| ===Trigonometry=== | |||
| The early ] on ] were translated and expanded in the ] by ] and ] mathematicians. {{Unicode|]}} produced tables of ] and ]s, and also developed ]. By the 10th century, in the work of ], Muslim mathematicians were using all six ]s, and had sine tables in 0.25° increments, to 8 decimal places of accuracy, as well as tables of ] values. Abū al-Wafā' also developed the trigonometric formula sin 2''x'' = 2 sin ''x'' cos ''x''. | |||
| ; Books on Islamic science | |||
| ] solved ]s using approximate numerical solutions found by interpolation in trigonometric tables. ], an Arabic mathematician in ], wrote the first treatise on ] in 1060. | |||
| * {{cite book|first1=Ali Abdullah al-|last1=Daffa|first2=J.J.|last2=Stroyls|title=Studies in the exact sciences in medieval Islam|publisher=Wiley|location=New York|year=1984|isbn=0-471-90320-5}} | |||
| * {{cite book|first=E. S.|last=Kennedy|author-link=Edward Stewart Kennedy|title=Studies in the Islamic Exact Sciences|year=1984|publisher=Syracuse Univ Press|isbn=0-8156-6067-7}} | |||
| ; Books on the history of mathematics | |||
| All of these earlier works on trigonometry treated it mainly as an adjunct to astronomy; perhaps the first treatment as a subject in its own right was by ] and ] (13th century). Nasir al-Din al-Tusi stated the ] and provided a proof for it, and also listed the six distinct cases of a right angled triangle in spherical trigonometry. | |||
| * {{cite book|last=Joseph|first=George Gheverghese|title=The Crest of the Peacock: Non-European Roots of Mathematics|edition=2nd|publisher=Princeton University Press|year=2000|isbn=0-691-00659-8|url=https://archive.org/details/crestofpeacockno00jose}} (Reviewed: {{cite journal|first1=Victor J.|last1=Katz|title='']'' by George Gheverghese Joseph|journal=The College Mathematics Journal|volume=23|issue=1|year=1992|pages=82–84|doi=10.2307/2686206|publisher=Mathematical Association of America|last2=Joseph|first2=George Gheverghese|jstor=2686206}}) | |||
| * {{cite book|last=Youschkevitch|first=Adolf P.|title=Gesichte der Mathematik im Mittelalter|publisher=BG Teubner Verlagsgesellschaft|location=Leipzig|year=1964}} | |||
| ;Journal articles on Islamic mathematics | |||
| ] (14th century) gives trigonometric tables of values of the sine function to four ] digits (equivalent to 8 decimal places) for each 1° of argument with differences to be added for each 1/60 of 1°. ] (14th century) also gives accurate tables of sines and tangents correct to 8 decimal places. | |||
| * Høyrup, Jens. . ''Filosofi og Videnskabsteori på Roskilde Universitetscenter''. 3. Række: ''Preprints og Reprints'' 1987 Nr. 1. | |||
| ;Bibliographies and biographies | |||
| The method of ], which was unknown in the ] world, was also first developed by Muslim mathematicians, who applied it to practical uses such as ].<ref>] (1996), "Engineering", in Roshdi Rashed, ''Encyclopedia of the History of Arabic Science'', Vol. 3, p. 751-795 .</ref> | |||
| * ]. ''Geschichte der Arabischen Litteratur''. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942. | |||
| * {{cite book|last=Sánchez Pérez|first=José A.|author-link=José Augusto Sánchez Pérez|title=Biografías de Matemáticos Árabes que florecieron en España|location=Madrid|publisher=Estanislao Maestre|year=1921}} | |||
| * {{cite book|last=Sezgin|first=Fuat|author-link=Fuat Sezgin|title=Geschichte Des Arabischen Schrifttums|publisher=Brill Academic Publishers|language=de|year=1997|isbn=90-04-02007-1}} | |||
| * {{cite book|last=Suter|first=Heinrich|author-link=Heinrich Suter|title=Die Mathematiker und Astronomen der Araber und ihre Werke|series=Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft|location=Leipzig|year=1900}} | |||
| ; Television documentaries | |||
| ==See also== | |||
| * ] (presenter) (2008). "The Genius of the East". '']''. ]. | |||
| *] | |||
| * ] (presenter) (2010). '']''. ]. | |||
| *] | |||
| {{Refend}} | |||
| *] | |||
| *] | |||
| *] | |||
| == |
==External links== | ||
| {{Commonscat|Mathematics of the Islamic Golden Age}} | |||
| <div class="references-2column"><references/></div> | |||
| *{{cite web|last=Hogendijk|first=Jan P.|author-link=Jan Hogendijk|date=January 1999|url=http://www.jphogendijk.nl/publ/Islamath.html|title=Bibliography of Mathematics in Medieval Islamic Civilization}} | |||
| *{{MacTutor|class=HistTopics|id=Arabic_mathematics|title=Arabic mathematics: forgotten brilliance?|year=1999}} | |||
| == References and further reading== | |||
| * | |||
| <div class="references-2column"> | |||
| * | |||
| *{{cite book|last=Berggren|first=J. Lennart|title=Episodes in the Mathematics of Medieval Islam|year=1986|publisher=Springer-Verlag|location=New York|id=ISBN 0-387-96318-9}}<!-- Reviewed: {{cite review|last=Toomer|first=Gerald J.|title=Episodes in the Mathematics of Medieval Islam|journal=American Mathematical Monthly|volume=95|issue=6|year=1988|url=http://links.jstor.org/sici?sici=0002-9890%28198806%2F07%2995%3A6%3C567%3AEITMOM%3E2.0.CO%3B2-3}}; {{cite review|first=Jan P.|last=Hogendijk|journal=Journal of the American Oriental Society|volume=109|issue=4|year=1989|pages=697-698}}.--> | |||
| {{History of mathematics}} | |||
| *{{cite book | |||
| | first=J. Lennart | |||
| | last=Berggren | |||
| | authorlink=Len Berggren | |||
| | editor=Victor J. Katz | |||
| | title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook | |||
| | chapter=Mathematics in Medieval Islam | |||
| | publisher=Princeton University Press | |||
| | year=2007 | |||
| | isbn=9780691114859 | |||
| }} | |||
| *{{cite book | |||
| | first=Carl B. | |||
| | last=Boyer | |||
| | authorlink=Carl Benjamin Boyer | |||
| | title=A History of Mathematics | |||
| | chapter=The Arabic Hegemony | |||
| | edition=Second Edition | |||
| | publisher=John Wiley & Sons, Inc | |||
| | year=1991 | |||
| | isbn=0471543977 | |||
| }} | |||
| *{{cite book | |||
| | first=Roger | |||
| | last=Cooke | |||
| | authorlink=Roger Cooke | |||
| | title=The History of Mathematics: A Brief Course | |||
| | chapter=Islamic Mathematics | |||
| | publisher=Wiley-Interscience | |||
| | year=1997 | |||
| | isbn=0471180823 | |||
| }} | |||
| *{{cite book|last=Daffa'|first=Ali Abdullah al-|title=The Muslim contribution to mathematics|year=1977|publisher=Croom Helm|location=London|id=ISBN 0-85664-464-1}} | |||
| * {{cite book|first=Ali Abdullah al-|last=Daffa|first2=J.J.|last2=Stroyls|title=Studies in the exact sciences in medieval Islam|publisher=Wiley|location=New York|year=1984|id=ISBN 0471903205}} | |||
| * {{cite book|last=Joseph|first=George Gheverghese|title=The Crest of the Peacock: Non-European Roots of Mathematics|edition=2nd Edition|publisher=Princeton University Press|year=2000|id=ISBN 0691006598}}<!-- Reviewed: {{Cite review|first=Victor J.|last=Katz|journal=The College Mathematics Journal|volume=23|issue=1|year=1992|pages=82-84}}.--> | |||
| * {{cite book|first=E. S.|last=Kennedy|title=Studies in the Islamic Exact Sciences|year=1984|publisher=Syracuse Univ Press|id=ISBN 0815660677}} | |||
| *{{cite book | |||
| | first=Kim | |||
| | last=Plofker | |||
| | authorlink=Kim Plofker | |||
| | editor=Victor J. Katz | |||
| | title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook | |||
| | chapter=Mathematics in India | |||
| | publisher=Princeton University Press | |||
| | year=2007 | |||
| | isbn=9780691114859 | |||
| }} | |||
| * {{MacTutor|class=HistTopics|id=Arabic_mathematics|title=Arabic mathematics: forgotten brilliance?|year=1999}} | |||
| * {{cite book|last=Rashed|first=Roshdi|others=Transl. by A. F. W. Armstrong|title=The Development of Arabic Mathematics: Between Arithmetic and Algebra|publisher=Springer|year=2001|id=ISBN 0792325656}} | |||
| * {{cite book|last=Sánchez Pérez|first=José A|title=Biografías de Matemáticos Árabes que florecieron en España|location=Madrid|publisher=Estanislao Maestre|year=1921}} | |||
| * {{cite book|last=Sezgin|first=Fuat|title=Geschichte Des Arabischen Schrifttums|publisher=Brill Academic Publishers|language=German|year=1997|id=ISBN 9004020071}} | |||
| * {{cite book|last=Suter|first=Heinrich|title=Die Mathematiker und Astronomen der Araber und ihre Werke|series=Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft|location=Leipzig|year=1900}} | |||
| * {{cite book|first=Adolf P.|last=Youschkevitch|coauthors=Boris A. Rozenfeld|title=Die Mathematik der Länder des Ostens im Mittelalter|year=1960|location=Berlin}} Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62-160. | |||
| * {{cite book|first=Adolf P.|last=Youschkevitch|title=Les mathématiques arabes: VIII<sup>e</sup>-XV<sup>e</sup> siècles|others=translated by M. Cazenave and K. Jaouiche|publisher=Vrin|location=Paris|year=1976|id=ISBN 978-2-7116-0734-1}} | |||
| </div> | |||
| == External links == | |||
| * Hogendijk, Jan P. (January 1999). . | |||
| {{Islamic mathematics}} | {{Islamic mathematics}} | ||
| {{Islamic studies}} | |||
| {{DEFAULTSORT:Mathematics In Medieval Islam}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 22:03, 7 January 2025

Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built upon syntheses of Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important developments of the period include extension of the place-value system to include decimal fractions, the systematised study of algebra and advances in geometry and trigonometry.
The medieval Islamic world underwent significant developments in mathematics. Muhammad ibn Musa al-Khwārizmī played a key role in this transformation, introducing algebra as a distinct field in the 9th century. Al-Khwārizmī's approach, departing from earlier arithmetical traditions, laid the groundwork for the arithmetization of algebra, influencing mathematical thought for an extended period. Successors like Al-Karaji expanded on his work, contributing to advancements in various mathematical domains. The practicality and broad applicability of these mathematical methods facilitated the dissemination of Arabic mathematics to the West, contributing substantially to the evolution of Western mathematics.
Arabic mathematical knowledge spread through various channels during the medieval era, driven by the practical applications of Al-Khwārizmī's methods. This dissemination was influenced not only by economic and political factors but also by cultural exchanges, exemplified by events such as the Crusades and the translation movement. The Islamic Golden Age, spanning from the 8th to the 14th century, marked a period of considerable advancements in various scientific disciplines, attracting scholars from medieval Europe seeking access to this knowledge. Trade routes and cultural interactions played a crucial role in introducing Arabic mathematical ideas to the West. The translation of Arabic mathematical texts, along with Greek and Roman works, during the 14th to 17th century, played a pivotal role in shaping the intellectual landscape of the Renaissance.
Origin and spread of Arab-Islamic mathematics
Arabic mathematics, particularly algebra, developed significantly during the medieval period. Muhammad ibn Musa al-Khwārizmī's (Arabic: محمد بن موسى الخوارزمي; c. 780 – c. 850) work between AD 813 and 833 in Baghdad was a turning point. He introduced the term "algebra" in the title of his book, "Kitab al-jabr wa al-muqabala," marking it as a distinct discipline. He regarded his work as "a short work on Calculation by (the rules of) Completion and Reduction, confining it to what is easiest and most useful in arithmetic". Later, people commented his work was not just a theoretical treatise but also practical, aimed at solving problems in areas like commerce and land measurement.
Al-Khwārizmī's approach was groundbreaking in that it did not arise from any previous "arithmetical" tradition, including that of Diophantus. He developed a new vocabulary for algebra, distinguishing between purely algebraic terms and those shared with arithmetic. Al-Khwārizmī noticed that the representation of numbers is crucial in daily life. Thus, he wanted to find or summarize a way to simplify the mathematical operation, so-called later, the algebra. His algebra was initially focused on linear and quadratic equations and the elementary arithmetic of binomials and trinomials. This approach, which involved solving equations using radicals and related algebraic calculations, influenced mathematical thinking long after his death.
Al-Khwārizmī's proof of the rule for solving quadratic equations of the form (ax^2 + bx = c), commonly referred to as "squares plus roots equal numbers," was a monumental achievement in the history of algebra. This breakthrough laid the groundwork for the systematic approach to solving quadratic equations, which became a fundamental aspect of algebra as it developed in the Western world. Al-Khwārizmī's method, which involved completing the square, not only provided a practical solution for equations of this type but also introduced an abstract and generalized approach to mathematical problems. His work, encapsulated in his seminal text "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala" (The Compendious Book on Calculation by Completion and Balancing), was translated into Latin in the 12th century. This translation played a pivotal role in the transmission of algebraic knowledge to Europe, significantly influencing mathematicians during the Renaissance and shaping the evolution of modern mathematics. Al-Khwārizmī's contributions, especially his proof for quadratic equations, are a testament to the rich mathematical heritage of the Islamic world and its enduring impact on Western mathematics.
The spread of Arabic mathematics to the West was facilitated by several factors. The practicality and general applicability of al-Khwārizmī's methods were significant. They were designed to convert numerical or geometrical problems into equations in normal form, leading to canonical solution formulae. His work and that of his successors like al-Karaji laid the foundation for advances in various mathematical fields, including number theory, numerical analysis, and rational Diophantine analysis.
Al-Khwārizmī's algebra was an autonomous discipline with its historical perspective, eventually leading to the "arithmetization of algebra". His successors expanded on his work, adapting it to new theoretical and technical challenges and reorienting it towards a more arithmetical direction for abstract algebraic calculation.
Arabic mathematics, epitomized by al-Khwārizmī's work, was crucial in shaping the mathematical landscape. Its spread to the West was driven by its practical applications, the expansion of mathematical concepts by his successors, and the translation and adaptation of these ideas into the Western context. This spread was a complex process involving economics, politics, and cultural exchange, greatly influencing Western mathematics.
The period known as the Islamic Golden Age (8th to 14th century) was characterized by significant advancements in various fields, including mathematics. Scholars in the Islamic world made substantial contributions to mathematics, astronomy, medicine, and other sciences. As a result, the intellectual achievements of Islamic scholars attracted the attention of scholars in medieval Europe who sought to access this wealth of knowledge. Trade routes, such as the Silk Road, facilitated the movement of goods, ideas, and knowledge between the East and West. Cities like Baghdad, Cairo, and Cordoba became centers of learning and attracted scholars from different cultural backgrounds. Therefore, mathematical knowledge from the Islamic world found its way to Europe through various channels. Meanwhile, the Crusades connected Western Europeans with the Islamic world. While the primary purpose of the Crusades was military, there was also cultural exchange and exposure to Islamic knowledge, including mathematics. European scholars who traveled to the Holy Land and other parts of the Islamic world gained access to Arabic manuscripts and mathematical treatises. During the 14th to 17th century, the translation of Arabic mathematical texts, along with Greek and Roman ones, played a crucial role in shaping the intellectual landscape of the Renaissance. Figures like Fibonacci, who studied in North Africa and the Middle East, helped introduce and popularize Arabic numerals and mathematical concepts in Europe.
Concepts

Algebra
Further information: History of algebraThe study of algebra, the name of which is derived from the Arabic word meaning completion or "reunion of broken parts", flourished during the Islamic golden age. Muhammad ibn Musa al-Khwarizmi, a Persian scholar in the House of Wisdom in Baghdad was the founder of algebra, is along with the Greek mathematician Diophantus, known as the father of algebra. In his book The Compendious Book on Calculation by Completion and Balancing, Al-Khwarizmi deals with ways to solve for the positive roots of first and second-degree (linear and quadratic) polynomial equations. He introduces the method of reduction, and unlike Diophantus, also gives general solutions for the equations he deals with.
Al-Khwarizmi's algebra was rhetorical, which means that the equations were written out in full sentences. This was unlike the algebraic work of Diophantus, which was syncopated, meaning that some symbolism is used. The transition to symbolic algebra, where only symbols are used, can be seen in the work of Ibn al-Banna' al-Marrakushi and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī.
On the work done by Al-Khwarizmi, J. J. O'Connor and Edmund F. Robertson said:
"Perhaps one of the most significant advances made by Arabic mathematics began at this time with the work of al-Khwarizmi, namely the beginnings of algebra. It is important to understand just how significant this new idea was. It was a revolutionary move away from the Greek concept of mathematics which was essentially geometry. Algebra was a unifying theory which allowed rational numbers, irrational numbers, geometrical magnitudes, etc., to all be treated as "algebraic objects". It gave mathematics a whole new development path so much broader in concept to that which had existed before, and provided a vehicle for the future development of the subject. Another important aspect of the introduction of algebraic ideas was that it allowed mathematics to be applied to itself in a way which had not happened before."
— MacTutor History of Mathematics archive
Several other mathematicians during this time period expanded on the algebra of Al-Khwarizmi. Abu Kamil Shuja' wrote a book of algebra accompanied with geometrical illustrations and proofs. He also enumerated all the possible solutions to some of his problems. Abu al-Jud, Omar Khayyam, along with Sharaf al-Dīn al-Tūsī, found several solutions of the cubic equation. Omar Khayyam found the general geometric solution of a cubic equation.
Cubic equations
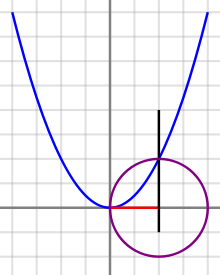
Omar Khayyam (c. 1038/48 in Iran – 1123/24) wrote the Treatise on Demonstration of Problems of Algebra containing the systematic solution of cubic or third-order equations, going beyond the Algebra of al-Khwārizmī. Khayyám obtained the solutions of these equations by finding the intersection points of two conic sections. This method had been used by the Greeks, but they did not generalize the method to cover all equations with positive roots.
Sharaf al-Dīn al-Ṭūsī (? in Tus, Iran – 1213/4) developed a novel approach to the investigation of cubic equations—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, to solve the equation , with a and b positive, he would note that the maximum point of the curve occurs at , and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than a. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.
| Part of a series on |
| Islamic studies |
|---|
| Jurisprudence |
| Science in medieval times |
| Arts |
| Other topics |
Induction
See also: Mathematical induction § HistoryThe earliest implicit traces of mathematical induction can be found in Euclid's proof that the number of primes is infinite (c. 300 BCE). The first explicit formulation of the principle of induction was given by Pascal in his Traité du triangle arithmétique (1665).
In between, implicit proof by induction for arithmetic sequences was introduced by al-Karaji (c. 1000) and continued by al-Samaw'al, who used it for special cases of the binomial theorem and properties of Pascal's triangle.
Irrational numbers
The Greeks had discovered irrational numbers, but were not happy with them and only able to cope by drawing a distinction between magnitude and number. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including Abū Kāmil Shujāʿ ibn Aslam and Ibn Tahir al-Baghdadi slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations. They worked freely with irrationals as mathematical objects, but they did not examine closely their nature.
In the twelfth century, Latin translations of Al-Khwarizmi's Arithmetic on the Indian numerals introduced the decimal positional number system to the Western world. His Compendious Book on Calculation by Completion and Balancing presented the first systematic solution of linear and quadratic equations. In Renaissance Europe, he was considered the original inventor of algebra, although it is now known that his work is based on older Indian or Greek sources. He revised Ptolemy's Geography and wrote on astronomy and astrology. However, C.A. Nallino suggests that al-Khwarizmi's original work was not based on Ptolemy but on a derivative world map, presumably in Syriac or Arabic.
Spherical trigonometry
Further information: Law of sines and History of trigonometryThe spherical law of sines was discovered in the 10th century: it has been attributed variously to Abu-Mahmud Khojandi, Nasir al-Din al-Tusi and Abu Nasr Mansur, with Abu al-Wafa' Buzjani as a contributor. Ibn Muʿādh al-Jayyānī's The book of unknown arcs of a sphere in the 11th century introduced the general law of sines. The plane law of sines was described in the 13th century by Nasīr al-Dīn al-Tūsī. In his On the Sector Figure, he stated the law of sines for plane and spherical triangles and provided proofs for this law.
Negative numbers
Further information: Negative numbersIn the 9th century, Islamic mathematicians were familiar with negative numbers from the works of Indian mathematicians, but the recognition and use of negative numbers during this period remained timid. Al-Khwarizmi did not use negative numbers or negative coefficients. But within fifty years, Abu Kamil illustrated the rules of signs for expanding the multiplication . Al-Karaji wrote in his book al-Fakhrī that "negative quantities must be counted as terms". In the 10th century, Abū al-Wafā' al-Būzjānī considered debts as negative numbers in A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen.
By the 12th century, al-Karaji's successors were to state the general rules of signs and use them to solve polynomial divisions. As al-Samaw'al writes:
the product of a negative number—al-nāqiṣ—by a positive number—al-zāʾid—is negative, and by a negative number is positive. If we subtract a negative number from a higher negative number, the remainder is their negative difference. The difference remains positive if we subtract a negative number from a lower negative number. If we subtract a negative number from a positive number, the remainder is their positive sum. If we subtract a positive number from an empty power (martaba khāliyya), the remainder is the same negative, and if we subtract a negative number from an empty power, the remainder is the same positive number.
Double false position
Further information: False position methodBetween the 9th and 10th centuries, the Egyptian mathematician Abu Kamil wrote a now-lost treatise on the use of double false position, known as the Book of the Two Errors (Kitāb al-khaṭāʾayn). The oldest surviving writing on double false position from the Middle East is that of Qusta ibn Luqa (10th century), an Arab mathematician from Baalbek, Lebanon. He justified the technique by a formal, Euclidean-style geometric proof. Within the tradition of Golden Age Muslim mathematics, double false position was known as hisāb al-khaṭāʾayn ("reckoning by two errors"). It was used for centuries to solve practical problems such as commercial and juridical questions (estate partitions according to rules of Quranic inheritance), as well as purely recreational problems. The algorithm was often memorized with the aid of mnemonics, such as a verse attributed to Ibn al-Yasamin and balance-scale diagrams explained by al-Hassar and Ibn al-Banna, who were each mathematicians of Moroccan origin.
Influences
The influence of medieval Arab-Islamic mathematics to the rest of the world is wide and profound, in both the realm of science and mathematics. The knowledge of the Arabs went into the western world through Spain and Sicily during the translation movement. "The Moors (western Mohammedans from that part of North Africa once known as Mauritania) crossed over into Spain early in the seventh century, bringing with them the cultural resources of the Arab world". In the 13th century, King Alfonso X of Castile established the Toledo School of Translators, in the Kingdom of Castile, where scholars translated numerous scientific and philosophical works from Arabic into Latin. The translations included Islamic contributions to trigonometry, which helps European mathematicians and astronomers in their studies. European scholars such as Gerard of Cremona (1114–1187) played a key role in translating and disseminating these works, thus making them accessible to a wider audience. Cremona is said to have translated into Latin "no fewer than 90 complete Arabic texts." European mathematicians, building on the foundations laid by Islamic scholars, further developed practical trigonometry for applications in navigation, cartography, and celestial navigation, thus pushing forward the age of discovery and scientific revolution. The practical applications of trigonometry for navigation and astronomy became increasingly important during the Age of Exploration.
Al-Battānī is one of the islamic mathematicians who made great contributions to the development of trigonometry. He "innovated new trigonometric functions, created a table of cotangents, and made some formulas in spherical trigonometry." These discoveries, together with his astronomical works which are praised for their accuracy, greatly advanced astronomical calculations and instruments.
Al-Khayyām (1048–1131) was a Persian mathematician, astronomer, and poet, known for his work on algebra and geometry, particularly his investigations into the solutions of cubic equations. He was "the first in history to elaborate a geometrical theory of equations with degrees ≤ 3", and has great influence on the work of Descartes, a French mathematician who is often regarded as the founder of analytical geometry. Indeed, "to read Descartes' Géométrie is to look upstream towards al-Khayyām and al-Ṭūsī; and downstream towards Newton, Leibniz, Cramer, Bézout and the Bernoulli brothers". Numerous problems that appear in "La Géométrie" (Geometry) have foundations that date back to al-Khayyām.
Abū Kāmil (Arabic: أبو كامل شجاع بن أسلم بن محمد بن شجاع, also known as Al-ḥāsib al-miṣrī—lit. "The Egyptian Calculator") (c. 850 – c. 930), was studied algebra following the author of Algebra, al-Khwārizmī. His Book of Algebra (Kitāb fī al-jabr wa al-muqābala) is "essentially a commentary on and elaboration of al-Khwārizmī's work; in part for that reason and in part for its own merit, the book enjoyed widespread popularity in the Muslim world". It contains 69 problems, which is more than al-Khwārizmī who had 40 in his book. Abū Kāmil's Algebra plays a significant role in shaping the trajectory of Western mathematics, particularly in its impact on the works of the Italian mathematician Leonardo of Pisa, widely recognized as Fibonacci. In his Liber Abaci (1202), Fibonacci extensively incorporated ideas from Arabic mathematicians, using approximately 29 problems from Book of Algebra with scarce modification.
Western historians' perception of the contribution of Arab mathematicians
Despite the fundamental works Arabic mathematicians have done on the development of Algebra and algebraic geometry, Western historians in the 18th and early 19th century still regarded it as a fact that Classical science and math were unique phenomena of the West. Even though some math contributions from Arab mathematicians are occasionally acknowledged, they are considered to be "outside history or only integrated in so far as it contributed to science, which is essentially European", and just some technical innovations to the Greek heritage rather than open up a completely new branch of mathematics. In the French philosopher Ernest Renan's work, Arabic math is merely "a reflection of Greece, combined with Persian and Indian influences". And according to Duhem, "Arabic science only reproduced the teachings received from Greek science". Besides being considered as merely some insignificant additions or reflections to the great tradition of Greek classical science, math works from Arabic mathematicians are also blamed for lacking rigor and too focused on practical applications and calculations, and this is why Western historians argued they could never reach the level of Greek mathematicians. As Tannery wrote, Arabic math "in no way superseded the level attained by Diophantus". On the other hand, they perceived that Western mathematicians went into a very different way both in its method employed and ultimate purpose, "the hallmark of Western science in its Greek origins as well as in its modern renaissance, is its conformity to rigorous standards". Thus, the perceived non-rigorous proof in Arabic mathematicians' book authorizes Bourbaki to exclude the Arabic period when he retraced the evolution of algebra. And instead, the history of classical algebra is written as the work of the Renaissance and the origin of algebraic geometry is traced back to Descartes, while Arabic mathematicians' contributions are ignored deliberately. In Rashed's words: "To justify the exclusion of science written in Arabic from the history of science, one invokes its absence of rigor, its calculatory appearance and its practical aims. Furthermore, strictly dependent on Greek science and, lastly, incapable of introducing experimental norms, scientists of that time were relegated to the role of conscientious guardians of the Hellenistic museum."
In 18th century Germany and France, the prevailing Orientalist view was "East and West oppose each other not as geographical but as historical positivities", which labeled "Rationalism" as the essence of the West, while the "Call of the Orient" movement emerged in the 19th century was interpreted as "against Rationalism" and a return to a more "spiritual and harmonious" lifestyle. Thus, the prevailing Orientalism in that period was one of the main reasons why Arabic mathematicians were often ignored for their contributions, as people outside the West were considered to be lacking the necessary rationality and scientific spirit to made significant contributions to math and science.
Conclusion
The medieval Arab-Islamic world played a crucial role in shaping the trajectory of mathematics, with al-Khwārizmī's algebraic innovations serving as a cornerstone. The dissemination of Arabic mathematics to the West during the Islamic Golden Age, facilitated by cultural exchanges and translations, left a lasting impact on Western mathematical thought. Mathematicians like Al-Battānī, Al-Khayyām, and Abū Kāmil, with their contributions to trigonometry, algebra, and geometry, extended their influence beyond their time. Despite the foundational contributions of Arab mathematicians, Western historians in the 18th and early 19th centuries, influenced by Orientalist views, sometimes marginalized these achievements. The East lacking rationality and scientific spirit perpetuated a biased perspective, hindering the recognition of the significant role played by Arabic mathematics in the development of algebra and other mathematical disciplines. Reevaluating the history of mathematics necessitates acknowledging the interconnectedness of diverse mathematical traditions and dispelling the notion of a uniquely European mathematical heritage. The contributions of Arab mathematicians, marked by practical applications and theoretical innovations, form an integral part of the rich tapestry of mathematical history, and deserves recognition.
Other major figures
- 'Abd al-Hamīd ibn Turk (fl. 830) (quadratics)
- Sind ibn Ali (d. after 864)
- Thabit ibn Qurra (826–901)
- Al-Battānī (before 858 – 929)
- Abū Kāmil (c. 850 – c. 930)
- Abu'l-Hasan al-Uqlidisi (fl. 952) (arithmetic)
- 'Abd al-'Aziz al-Qabisi (d. 967)
- Abū Sahl al-Qūhī (c. 940–1000) (centres of gravity)
- Ibn al-Haytham (c. 965–1040)
- Abū al-Rayḥān al-Bīrūnī (973–1048) (trigonometry)
- Al-Khayyām (1048–1131)
- Ibn Maḍāʾ (c. 1116–1196)
- Ismail al-Jazari (1136–1206)
- Jamshīd al-Kāshī (c. 1380–1429) (decimals and estimation of the circle constant)
Gallery
-
 Engraving of Abū Sahl al-Qūhī's perfect compass to draw conic sections
Engraving of Abū Sahl al-Qūhī's perfect compass to draw conic sections
-
The theorem of Ibn Haytham
See also
- Arabic numerals
- Indian influence on Islamic mathematics in medieval Islam
- History of calculus
- History of geometry
- Science in the medieval Islamic world
- Timeline of science and engineering in the Muslim world
References
- Katz (1993): "A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied... Still, the general outline... is known. In particular, Islamic mathematicians fully developed the decimal place-value number system to include decimal fractions, systematised the study of algebra and began to consider the relationship between algebra and geometry, studied and made advances on the major Greek geometrical treatises of Euclid, Archimedes, and Apollonius, and made significant improvements in plane and spherical geometry."
^ Smith (1958), Vol. 1, Chapter VII.4: "In a general way it may be said that the Golden Age of Arabian mathematics was confined largely to the 9th and 10th centuries; that the world owes a great debt to Arab scholars for preserving and transmitting to posterity the classics of Greek mathematics; and that their work was chiefly that of transmission, although they developed considerable originality in algebra and showed some genius in their work in trigonometry." - Lumpkin, Beatrice; Zitler, Siham (1992). "Cairo: Science Academy of the Middle Ages". In Van Sertima, Ivan (ed.). Golden age of the Moor, Volume 11. Transaction Publishers. p. 394. ISBN 1-56000-581-5. "The Islamic mathematicians exercised a prolific influence on the development of science in Europe, enriched as much by their own discoveries as those they had inherited by the Greeks, the Indians, the Syrians, the Babylonians, etc."
- ^ ben Musa, Mohammed (2013-03-28). The Algebra of Mohammed ben Musa. Cambridge University Press. ISBN 978-1-108-05507-9.
- ^ Swetz, Frank J. (2012-08-15). Mathematical Treasures: Mesopotamian Accounting Tokens (Report). Washington, DC: The MAA Mathematical Sciences Digital Library.
- "Extending al-Karaji's Work on Sums of Odd Powers of Integers - Introduction | Mathematical Association of America". maa.org. Retrieved 2023-12-15.
- "algebra". Online Etymology Dictionary.
- Boyer 1991, p. 228.
- Swetz, Frank J. (1993). Learning Activities from the History of Mathematics. Walch Publishing. p. 26. ISBN 978-0-8251-2264-4.
- ^ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.
- O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics Archive, University of St Andrews
- O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics Archive, University of St Andrews
- Struik 1987, p. 96.
- ^ Boyer 1991, pp. 241–242.
- Struik 1987, p. 97.
- Berggren, J. Lennart; Al-Tūsī, Sharaf Al-Dīn; Rashed, Roshdi (1990). "Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's al-Muʿādalāt". Journal of the American Oriental Society. 110 (2): 304–309. doi:10.2307/604533. JSTOR 604533.
- ^ Sesiano, Jacques (2000). "Islamic Mathematics". In Selin, Helaine (ed.). Mathematics Across Cultures: The History of Non-Western Mathematics. Springer Netherlands. pp. 137–165. doi:10.1007/978-94-011-4301-1_9. ISBN 978-94-011-4301-1.
- O'Connor, John J.; Robertson, Edmund F., "Abu Mansur ibn Tahir Al-Baghdadi", MacTutor History of Mathematics Archive, University of St Andrews
- Allen, G. Donald (n.d.). "The History of Infinity" (PDF). Texas A&M University. Retrieved 7 September 2016.
- Struik 1987, p. 93
- Rosen 1831, p. v–vi.
- Toomer, Gerald (1990). "Al-Khwārizmī, Abu Ja'far Muḥammad ibn Mūsā". In Gillispie, Charles Coulston (ed.). Dictionary of Scientific Biography. Vol. 7. New York: Charles Scribner's Sons. ISBN 0-684-16962-2 – via Encyclopedia.com.
- Nallino 1939.
- O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", MacTutor History of Mathematics Archive, University of St Andrews
- Berggren 2007, p. 518.
- ^ Rashed, R. (1994-06-30). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Springer. pp. 36–37. ISBN 9780792325659.
- ^ Mat Rofa Bin Ismail (2008), "Algebra in Islamic Mathematics", in Helaine Selin (ed.), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, vol. 1 (2nd ed.), Springer, p. 115, ISBN 9781402045592
- Schwartz, R. K. (2004). Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position) (PDF). Eighth North African Meeting on the History of Arab Mathematics. Radès, Tunisia. Archived from the original (PDF) on 2014-05-16. Retrieved 2012-06-08. "Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position)". Archived from the original (.doc) on 2011-09-15.
- ^ Masters, Barry R. (2011-06-08). "Biomedical ethics, 7th edition David DeGrazia, Thomas A. Mappes, Jeffrey Brand-Ballard: 2010, Softcover, 732pp, ISBN-9780073407456 £171.15 McGraw-Hill Incorporated". Graefe's Archive for Clinical and Experimental Ophthalmology. 250 (1): 159–160. doi:10.1007/s00417-011-1640-x. ISSN 0721-832X.
- "Edited by", Contributions to Non-Standard Analysis, Elsevier, pp. iii, 1972, retrieved 2023-12-15
- ^ Rashed, Roshdi (2014-08-21). Classical Mathematics from Al-Khwarizmi to Descartes. Routledge. ISBN 978-1-317-62239-0.
- ^ Masters, Barry R. (2011-06-08). "Biomedical ethics, 7th edition David DeGrazia, Thomas A. Mappes, Jeffrey Brand-Ballard: 2010, Softcover, 732pp, ISBN-9780073407456 £171.15 McGraw-Hill Incorporated". Graefe's Archive for Clinical and Experimental Ophthalmology. 250 (1): 159–160. doi:10.1007/s00417-011-1640-x. ISSN 0721-832X.
- ^ Rashed, Roshdi (1994). "The Development of Arabic Mathematics: Between Arithmetic and Algebra". Boston Studies in the Philosophy of Science. doi:10.1007/978-94-017-3274-1. ISSN 0068-0346.
Sources
- Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". In Victor J. Katz (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-11485-9.
- Boyer, Carl B. (1991), "Greek Trigonometry and Mensuration, and The Arabic Hegemony", A History of Mathematics (2nd ed.), New York City: John Wiley & Sons, ISBN 0-471-54397-7
- Katz, Victor J. (1993). A History of Mathematics: An Introduction. HarperCollins college publishers. ISBN 0-673-38039-4.
- Nallino, C.A. (1939), "Al-Ḥuwārismī e il suo rifacimento della Geografia di Tolomeo", Raccolta di scritti editi e inediti (in Italian), vol. V, Rome: Istituto per l'Oriente, pp. 458–532
- Rosen, Fredrick (1831). The Algebra of Mohammed Ben Musa. Kessinger Publishing. ISBN 1-4179-4914-7.
- Smith, David E. (1958). History of Mathematics. Dover Publications. ISBN 0-486-20429-4.
- Struik, Dirk J. (1987), A Concise History of Mathematics (4th rev. ed.), Dover Publications, ISBN 0-486-60255-9
Further reading
- Books on Islamic mathematics
- Berggren, J. Lennart (1986). Episodes in the Mathematics of Medieval Islam. New York: Springer-Verlag. ISBN 0-387-96318-9.
- Review: Toomer, Gerald J.; Berggren, J. L. (1988). "Episodes in the Mathematics of Medieval Islam". American Mathematical Monthly. 95 (6). Mathematical Association of America: 567. doi:10.2307/2322777. JSTOR 2322777.
- Review: Hogendijk, Jan P.; Berggren, J. L. (1989). "Episodes in the Mathematics of Medieval Islam by J. Lennart Berggren". Journal of the American Oriental Society. 109 (4). American Oriental Society: 697–698. doi:10.2307/604119. JSTOR 604119.
- Daffa', Ali Abdullah al- (1977). The Muslim contribution to mathematics. London: Croom Helm. ISBN 0-85664-464-1.
- Ronan, Colin A. (1983). The Cambridge Illustrated History of the World's Science. Cambridge University Press. ISBN 0-521-25844-8.
- Rashed, Roshdi (2001). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Translated by A. F. W. Armstrong. Springer. ISBN 0-7923-2565-6.
- Youschkevitch, Adolf P.; Rozenfeld, Boris A. (1960). Die Mathematik der Länder des Ostens im Mittelalter. Berlin.
{{cite book}}: CS1 maint: location missing publisher (link) Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160. - Youschkevitch, Adolf P. (1976). Les mathématiques arabes: VIII–XV siècles. translated by M. Cazenave and K. Jaouiche. Paris: Vrin. ISBN 978-2-7116-0734-1.
- Book chapters on Islamic mathematics
- Lindberg, D.C., and M. H. Shank, eds. The Cambridge History of Science. Volume 2: Medieval Science (Cambridge UP, 2013), chapters 2 and 3 mathematics in Islam.
- Cooke, Roger (1997). "Islamic Mathematics". The History of Mathematics: A Brief Course. Wiley-Interscience. ISBN 0-471-18082-3.
- Books on Islamic science
- Daffa, Ali Abdullah al-; Stroyls, J.J. (1984). Studies in the exact sciences in medieval Islam. New York: Wiley. ISBN 0-471-90320-5.
- Kennedy, E. S. (1984). Studies in the Islamic Exact Sciences. Syracuse Univ Press. ISBN 0-8156-6067-7.
- Books on the history of mathematics
- Joseph, George Gheverghese (2000). The Crest of the Peacock: Non-European Roots of Mathematics (2nd ed.). Princeton University Press. ISBN 0-691-00659-8. (Reviewed: Katz, Victor J.; Joseph, George Gheverghese (1992). "The Crest of the Peacock: Non-European Roots of Mathematics by George Gheverghese Joseph". The College Mathematics Journal. 23 (1). Mathematical Association of America: 82–84. doi:10.2307/2686206. JSTOR 2686206.)
- Youschkevitch, Adolf P. (1964). Gesichte der Mathematik im Mittelalter. Leipzig: BG Teubner Verlagsgesellschaft.
- Journal articles on Islamic mathematics
- Høyrup, Jens. “The Formation of «Islamic Mathematics»: Sources and Conditions”. Filosofi og Videnskabsteori på Roskilde Universitetscenter. 3. Række: Preprints og Reprints 1987 Nr. 1.
- Bibliographies and biographies
- Brockelmann, Carl. Geschichte der Arabischen Litteratur. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942.
- Sánchez Pérez, José A. (1921). Biografías de Matemáticos Árabes que florecieron en España. Madrid: Estanislao Maestre.
- Sezgin, Fuat (1997). Geschichte Des Arabischen Schrifttums (in German). Brill Academic Publishers. ISBN 90-04-02007-1.
- Suter, Heinrich (1900). Die Mathematiker und Astronomen der Araber und ihre Werke. Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft. Leipzig.
{{cite book}}: CS1 maint: location missing publisher (link)
- Television documentaries
- Marcus du Sautoy (presenter) (2008). "The Genius of the East". The Story of Maths. BBC.
- Jim Al-Khalili (presenter) (2010). Science and Islam. BBC.
External links
- Hogendijk, Jan P. (January 1999). "Bibliography of Mathematics in Medieval Islamic Civilization".
- O'Connor, John J.; Robertson, Edmund F. (1999), "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics Archive, University of St Andrews
- Richard Covington, Rediscovering Arabic Science, 2007, Saudi Aramco World
- List of Inventions and Discoveries in Mathematics During the Islamic Golden Age
| History of mathematics (timeline) | |
|---|---|
| By topic |
|
| Numeral systems | |
| By ancient cultures | |
| Controversies | |
| Other |
|
| Mathematics in the medieval Islamic world | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mathematicians |
|  | ||||||||||||||||
| Mathematical works | ||||||||||||||||||
| Concepts | ||||||||||||||||||
| Centers | ||||||||||||||||||
| Influences | ||||||||||||||||||
| Influenced | ||||||||||||||||||
| Related | ||||||||||||||||||
| Islamic studies | |
|---|---|
| Arts | |
| Economics | |
| History | |
| Law and politics | |
| Philosophy | |
| Medieval science | |
| Other fields | |
 , with a and b positive, he would note that the maximum point of the curve
, with a and b positive, he would note that the maximum point of the curve  occurs at
occurs at  , and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than a. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.
, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than a. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.
 .
.