| Revision as of 19:02, 22 July 2023 editJacobolus (talk | contribs)Extended confirmed users35,791 editsmNo edit summary← Previous edit | Latest revision as of 16:41, 26 July 2024 edit undoCitation bot (talk | contribs)Bots5,454,177 edits Altered pages. Added isbn. Formatted dashes. | Use this bot. Report bugs. | Suggested by Abductive | Category:Spherical curves | #UCB_Category 6/14 | ||
| (26 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Mathematical expression of circle like slices of sphere}} | {{short description|Mathematical expression of circle like slices of sphere}} | ||
| {{Redirect|Small circle|the typographical symbol|Degree symbol}} | {{Redirect|Small circle|the typographical symbol|Degree symbol}} | ||
| {{inline |date=May 2024}} | |||
| ] | ] | ||
| ⚫ | ] | ||
| In ], a '''spherical circle''' (often shortened to '''circle''') is the ] of ]s on a ] at constant ] (the '' |
In ], a '''spherical circle''' (often shortened to '''circle''') is the ] of ]s on a ] at constant ] (the ''spherical radius'') from a given point on the sphere (the ''pole'' or ''spherical center''). It is a ] of constant ] relative to the sphere, analogous to a ] in the ]; the curves analogous to ] are called '']s'', and the curves analogous to planar ]s are called '''small circles''' or '''lesser circles'''. If the sphere is embedded in three-dimensional ], its circles are the ] of the sphere with ], and the great circles are intersections with planes passing through the ] of the sphere. | ||
| == Fundamental concepts == | |||
| ⚫ | A circle with zero curvature |
||
| === Intrinsic characterization === | |||
| ⚫ | A circle with non-zero curvature |
||
| ⚫ | A spherical circle with zero geodesic curvature is called a ''great circle'', and is a ] analogous to a straight line in the plane. A great circle separates the sphere into two equal '']'', each with the great circle as its boundary. If a great circle passes through a point on the sphere, it also passes through the ] (the unique furthest other point on the sphere). For any pair of distinct non-antipodal points, a unique great circle passes through both. Any two points on a great circle separate it into two ''arcs'' analogous to ]s in the plane; the shorter is called the ''minor arc'' and is the shortest path between the points, and the longer is called the ''major arc''. | ||
| ⚫ | Every circle has two antipodal |
||
| ⚫ | A circle with non-zero geodesic curvature is called a ''small circle'', and is analogous to a circle in the plane. A small circle separates the sphere into two ''spherical disks'' or '']s'', each with the circle as its boundary. For any triple of distinct non-antipodal points a unique small circle passes through all three. Any two points on the small circle separate it into two ''arcs'', analogous to ]s in the plane. | ||
| ⚫ | If the sphere is ] in ], the sphere's ] with a ] is a circle, which can |
||
| ⚫ | Every circle has two antipodal poles (or centers) intrinsic to the sphere. A great circle is equidistant to its poles, while a small circle is closer to one pole than the other. ] circles are sometimes called ''parallels'', because they each have constant distance to each-other, and in particular to their concentric great circle, and are in that sense analogous to ]s in the plane. | ||
| ⚫ | The sphere's intersection with a second sphere is also a circle, and the sphere's intersection with a concentric ] or ] is a pair of antipodal circles. | ||
| === Extrinsic characterization === | |||
| ==On the earth== | |||
| ⚫ | ] | ||
| ⚫ | In the ] on a globe, the ] of ] are small circles, with the ] the only great circle. By contrast, all ] of ], paired with their opposite meridian in the other ], form great circles. | ||
| ⚫ | If the sphere is ] ] in ], the sphere's ] with a ] is a circle, which can be interpreted extrinsically to the sphere as a Euclidean circle: a locus of points in the plane at a constant ] (the ''extrinsic radius'') from a point in the plane (the ''extrinsic center''). A great circle lies on a plane passing through the center of the sphere, so its extrinsic radius is equal to the radius of the sphere itself, and its extrinsic center is the sphere's center. A small circle lies on a plane ''not'' passing through the sphere's center, so its extrinsic radius is smaller than that of the sphere and its extrinsic center is an arbitrary point in the interior of the sphere. Parallel planes cut the sphere into parallel (concentric) small circles; the pair of parallel planes tangent to the sphere are tangent at the poles of these circles, and the ] through these poles, passing through the sphere's center and perpendicular to the parallel planes, is called the ''axis'' of the parallel circles. | ||
| ==Related terminology== | |||
| The diameter of the sphere which passes through the center of the circle is called its '''axis''' and the endpoints of this diameter are called its '''poles'''. A '''circle of a sphere''' can also be defined as the set of points at a given ] from a given pole. | |||
| ⚫ | The sphere's intersection with a second sphere is also a circle, and the sphere's intersection with a concentric ] or ] is a pair of antipodal circles. | ||
| ==Sphere-plane intersection== | |||
| When the intersection of a sphere and a plane is not empty or a single point, it is a circle. This can be seen as follows: | |||
| == Applications == | |||
| Let ''S'' be a sphere with center ''O'', ''P'' a plane which intersects ''S''. Draw {{overline|''OE''}} perpendicular to ''P'' and meeting ''P'' at ''E''. Let ''A'' and ''B'' be any two different points in the intersection. Then ''AOE'' and ''BOE'' are right triangles with a common side, ''OE'', and hypotenuses ''AO'' and ''BO'' equal. Therefore, the remaining sides ''AE'' and ''BE'' are equal. This proves that all points in the intersection are the same distance from the point ''E'' in the plane ''P'', in other words all points in the intersection lie on a circle ''C'' with center ''E''.<ref>Proof follows Hobbs, Prop. 304</ref> This proves that the intersection of ''P'' and ''S'' is contained in ''C''. Note that ''OE'' is the axis of the circle. | |||
| === Geodesy === | |||
| ⚫ | In the ] on a globe, the ] of ] are small circles, with the ] the only great circle. By contrast, all ] of ], paired with their opposite meridian in the other ], form great circles. | ||
| ⚫ | == References == | ||
| Now consider a point ''D'' of the circle ''C''. Since ''C'' lies in ''P'', so does ''D''. On the other hand, the triangles ''AOE'' and ''DOE'' are right triangles with a common side, ''OE'', and legs ''EA'' and ''ED'' equal. Therefore, the hypotenuses ''AO'' and ''DO'' are equal, and equal to the radius of ''S'', so that ''D'' lies in ''S''. This proves that ''C'' is contained in the intersection of ''P'' and ''S''. | |||
| * {{cite journal |mode=cs2 |last= | |||
| Allardice |first=Robert Edgar |author-link=Robert Edgar Allardice |year= | |||
| 1883 |title=Spherical Geometry |journal=Proceedings of the Edinburgh Mathematical Society |volume=2 |pages=8–16 |doi=10.1017/S0013091500037020 |doi-access=free }} <!-- hathi trust: https://babel.hathitrust.org/cgi/pt?id=inu.30000021035997&view=1up&seq=16 --> | |||
| ⚫ | * {{cite book |mode=cs2 |last= | ||
| Casey |first=John |author-link=John Casey (mathematician) |year= | |||
| 1889 |title=A treatise on spherical trigonometry |publisher=Hodges, Figgis, & co. |isbn= | |||
| ⚫ | 978-1-4181-8047-8 |url=https://archive.org/details/treatiseonspheri00seri/ }} | ||
| * {{cite journal |mode=cs2 |last= | |||
| Papadopoulos |first=Athanase |author-link=Athanase Papadopoulos |year= | |||
| 2014 |title=On the works of Euler and his followers on spherical geometry |journal=Gaṇita Bhārati |volume=36 |pages=53–108 |arxiv=1409.4736 }} | |||
| * {{cite book |mode=cs2 |last1= | |||
| Todhunter |first1=Isaac |authorlink1=Isaac Todhunter |last2= | |||
| Leathem |first2=John Gaston |year= | |||
| 1901 |title=Spherical Trigonometry |edition=Revised |publisher=MacMillan |url=https://archive.org/details/sphericaltrigono00todh/ }} | |||
| ⚫ | ] | ||
| As a corollary, on a sphere there is exactly one circle that can be drawn through three given points.<ref>Hobbs, Prop. 308</ref> | |||
| ⚫ | ] | ||
| The proof can be extended to show that the points on a circle are all a common angular distance from one of its poles.<ref>Hobbs, Prop. 310</ref> | |||
| {{geometry stub}} | |||
| Compare also ]s, which can produce ]s. | |||
| ==Sphere-sphere intersection== | |||
| To show that a non-trivial intersection of two spheres is a circle, assume (without loss of generality) that one sphere (with radius <math>R</math>) is centered at the origin. Points on this sphere satisfy | |||
| :<math>x^2 + y^2 + z^2 = R^2.</math> | |||
| Also without loss of generality, assume that the second sphere, with radius <math>r</math>, is centered at a point on the positive x-axis, at distance <math>a</math> from the origin. Its points satisfy | |||
| :<math>(x-a)^2 + y^2 + z^2 = r^2.</math> | |||
| The intersection of the spheres is the set of points satisfying both equations. Subtracting the equations gives | |||
| :<math>\begin{align} | |||
| (x-a)^2 - x^2 & = r^2 - R^2 \\ | |||
| a^2 - 2ax & = r^2 - R^2 \\ | |||
| x & = \frac{a^2 + R^2 - r^2}{2a}. | |||
| \end{align}</math> | |||
| In the singular case <math>a = 0</math>, the spheres are concentric. There are two possibilities: if <math>R = r</math>, the spheres coincide, and the intersection is the entire sphere; if <math>R \not= r</math>, the spheres are disjoint and the intersection is empty. | |||
| When ''a'' is nonzero, the intersection lies in a vertical plane with this x-coordinate, which may intersect both of the spheres, be tangent to both spheres, or external to both spheres. | |||
| The result follows from the previous proof for sphere-plane intersections. | |||
| ==See also== | |||
| *] | |||
| *] | |||
| ⚫ | ==References== | ||
| {{reflist}} | |||
| *{{cite book |title=Solid Geometry|url=https://archive.org/details/solidgeometry00hobbgoog|first=C.A.|last=Hobbs|publisher=G.H. Kent|year=1921|pages= ff}} | |||
| ==Further reading== | |||
| ⚫ | *{{cite book | |
||
| ⚫ | |url=https://archive.org/details/ |
||
| |first1=M.|last1=Sykes|first2=C.E.|last2=Comstock|publisher=Rand McNally | |||
| |year=1922|pages= ff}} | |||
| ] | |||
| ⚫ | ] | ||
| ⚫ | ] | ||
Latest revision as of 16:41, 26 July 2024
Mathematical expression of circle like slices of sphere "Small circle" redirects here. For the typographical symbol, see Degree symbol.| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (May 2024) (Learn how and when to remove this message) |

In spherical geometry, a spherical circle (often shortened to circle) is the locus of points on a sphere at constant spherical distance (the spherical radius) from a given point on the sphere (the pole or spherical center). It is a curve of constant geodesic curvature relative to the sphere, analogous to a line or circle in the Euclidean plane; the curves analogous to straight lines are called great circles, and the curves analogous to planar circles are called small circles or lesser circles. If the sphere is embedded in three-dimensional Euclidean space, its circles are the intersections of the sphere with planes, and the great circles are intersections with planes passing through the center of the sphere.
Fundamental concepts
Intrinsic characterization
A spherical circle with zero geodesic curvature is called a great circle, and is a geodesic analogous to a straight line in the plane. A great circle separates the sphere into two equal hemispheres, each with the great circle as its boundary. If a great circle passes through a point on the sphere, it also passes through the antipodal point (the unique furthest other point on the sphere). For any pair of distinct non-antipodal points, a unique great circle passes through both. Any two points on a great circle separate it into two arcs analogous to line segments in the plane; the shorter is called the minor arc and is the shortest path between the points, and the longer is called the major arc.
A circle with non-zero geodesic curvature is called a small circle, and is analogous to a circle in the plane. A small circle separates the sphere into two spherical disks or spherical caps, each with the circle as its boundary. For any triple of distinct non-antipodal points a unique small circle passes through all three. Any two points on the small circle separate it into two arcs, analogous to circular arcs in the plane.
Every circle has two antipodal poles (or centers) intrinsic to the sphere. A great circle is equidistant to its poles, while a small circle is closer to one pole than the other. Concentric circles are sometimes called parallels, because they each have constant distance to each-other, and in particular to their concentric great circle, and are in that sense analogous to parallel lines in the plane.
Extrinsic characterization
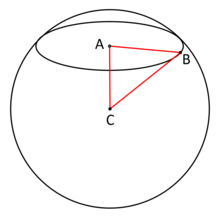
If the sphere is isometrically embedded in Euclidean space, the sphere's intersection with a plane is a circle, which can be interpreted extrinsically to the sphere as a Euclidean circle: a locus of points in the plane at a constant Euclidean distance (the extrinsic radius) from a point in the plane (the extrinsic center). A great circle lies on a plane passing through the center of the sphere, so its extrinsic radius is equal to the radius of the sphere itself, and its extrinsic center is the sphere's center. A small circle lies on a plane not passing through the sphere's center, so its extrinsic radius is smaller than that of the sphere and its extrinsic center is an arbitrary point in the interior of the sphere. Parallel planes cut the sphere into parallel (concentric) small circles; the pair of parallel planes tangent to the sphere are tangent at the poles of these circles, and the diameter through these poles, passing through the sphere's center and perpendicular to the parallel planes, is called the axis of the parallel circles.
The sphere's intersection with a second sphere is also a circle, and the sphere's intersection with a concentric right circular cylinder or right circular cone is a pair of antipodal circles.
Applications
Geodesy
In the geographic coordinate system on a globe, the parallels of latitude are small circles, with the Equator the only great circle. By contrast, all meridians of longitude, paired with their opposite meridian in the other hemisphere, form great circles.
References
- Allardice, Robert Edgar (1883), "Spherical Geometry", Proceedings of the Edinburgh Mathematical Society, 2: 8–16, doi:10.1017/S0013091500037020
- Casey, John (1889), A treatise on spherical trigonometry, Hodges, Figgis, & co., ISBN 978-1-4181-8047-8
- Papadopoulos, Athanase (2014), "On the works of Euler and his followers on spherical geometry", Gaṇita Bhārati, 36: 53–108, arXiv:1409.4736
- Todhunter, Isaac; Leathem, John Gaston (1901), Spherical Trigonometry (Revised ed.), MacMillan
This geometry-related article is a stub. You can help Misplaced Pages by expanding it. |
 , where C is the center of the sphere, A is the center of the small circle, and B is a point in the boundary of the small circle. Therefore, knowing the radius of the sphere, and the distance from the plane of the small circle to C, the radius of the small circle can be determined using the Pythagorean theorem.
, where C is the center of the sphere, A is the center of the small circle, and B is a point in the boundary of the small circle. Therefore, knowing the radius of the sphere, and the distance from the plane of the small circle to C, the radius of the small circle can be determined using the Pythagorean theorem.