| Revision as of 09:07, 10 March 2006 editArt Carlson (talk | contribs)Extended confirmed users, Pending changes reviewers5,350 edits →"Reddening" due to scattering: shifts on the order of the line width← Previous edit | Revision as of 12:53, 10 March 2006 edit undoජපස (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers60,575 edits rv -- Wolf Effect can be described on its own page, but due to undue weight does not belong here.Next edit → | ||
| Line 67: | Line 67: | ||
| In many circumstances scattering causes the radiation to redden because ] results in the predominance of many low ] photons over few high energy ones (while conserving total energy). Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated ''z'' is generally a ] of wavelength. Furthermore, scattering from ] ] generally occurs at many ]s, and ''z'' is also a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of ]s as well. | In many circumstances scattering causes the radiation to redden because ] results in the predominance of many low ] photons over few high energy ones (while conserving total energy). Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated ''z'' is generally a ] of wavelength. Furthermore, scattering from ] ] generally occurs at many ]s, and ''z'' is also a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of ]s as well. | ||
| In ], ] can appear ] due to scattering processes in a phenomenon referred to as ] — the same effect that causes the ] reddening of the ] seen in the ] or ] and causes the rest of the ] to have a ] ]. This phenomenon is distinct from red''shift''ing because the ] are not shifted to other wavelengths in reddened objects |
In ], ] can appear ] due to scattering processes in a phenomenon referred to as ] — the same effect that causes the ] reddening of the ] seen in the ] or ] and causes the rest of the ] to have a ] ]. This phenomenon is distinct from red''shift''ing because the ] are not shifted to other wavelengths in reddened objects and there is an additional ] and distortion associated with the phenomenon due to photons being scattered in and out of the ]. | ||
| ''For a list of scattering processes, see ].'' | ''For a list of scattering processes, see ].'' | ||
Revision as of 12:53, 10 March 2006
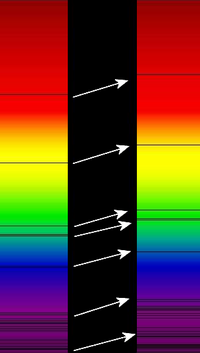
- This article is about the optical phenomenon. For the photochemical usage, see bathochromic shift. For other uses of the phrase "Red Shift", see Red Shift.
In physics and astronomy, redshift is an observed increase in the wavelength of electromagnetic radiation received by a detector compared to that emitted by the source. For visible light, red is the color with the longest wavelength, so colors experiencing redshift shift towards the red part of the electromagnetic spectrum. The phenomenon goes by the same name even if it occurs at non-optical wavelengths (in fact, longer-wavelength radiation "redshifts" away from red). The corresponding shift to shorter wavelengths is called blueshift.
Astrophysical redshift occurs, for example, when a light source moves away from an observer in an analogous but not equivalent fashion to a Doppler shift of sound waves from a receding object. Redshift is used as a diagnostic in spectroscopic astrophysics to determine information about the dynamics and kinematics of distant objects. Most famously, redshifts are observed in the spectra from distant galaxies, quasars, and intergalactic gas clouds to increase proportionally with the distance to the object. Astronomers consider this to be one of the major forms of evidence that the universe is expanding, supporting the Big Bang model.
The relative change in wavelength z
A redshift (or blueshift) may be characterized by the difference between the observed and emitted wavelengths. In astronomy it is customary to refer to the relative change in wavelength, a dimensionless quantity called z and defined by the equation
where is the wavelength of electromagnetic radiation.
One advantage of using z is that it is independent of the wavelength observed for Doppler-like redshifts (see below), which is the most common usage of the term redshift.
The increase in wavelength of a photon subjected to a redshift corresponds to a decrease in its frequency,
where is the frequency of electromagnetic radiation.
Sometimes it is preferable to use the form
Classical redshift mechanisms
A redshift can occur in a vacuum, without any direct interaction with intervening matter in three ways. Each of these mechanisms produces a Doppler-like redshift, meaning that z is independent of wavelength.
Doppler effect
If a source of the light is moving away from an observer, then redshift (z > 0) occurs; if the source moves towards the observer, then blueshift (z < 0) occurs. This is true for all electromagnetic waves and is explained by the Doppler effect. Consequently, this type of redshift is also called the Doppler redshift. If the source moves away from the observer with velocity v, then, ignoring relativistic effects, the redshift is given by
where c is the speed of light. For a more complete discussion on the origin of the frequency shift, see the article on the relativistic Doppler effect. In the classical Doppler effect, the frequency of the source is not modified, but the recessional motion causes the illusion of a lower frequency.
Expansion of space
An effect very similar to the Doppler effect is caused by the expansion of space predicted by the current models of physical cosmology. Again, the properties of the source are not modified, but the photons will be stretched as the space through which it is traveling expands, which increases the wavelength. This effect is predicted by the current cosmological model as an observable manifestation of the time-dependent cosmic scale factor () in the following way:
This type of redshift is also called the cosmological redshift or Hubble redshift. If the Universe were contracting instead of expanding, we would see distant galaxies blueshifted by an amount proportional to their distance instead of redshifted. This is relevant to the old conundrum known as Olbers' paradox: if the Universe were static and filled with a uniform distribution of stars, then every line of sight in the sky would end on a star, and the sky would be uniformly bright. (In fact, if the Universe were infinitely large, then by this reasoning, the entire sky would be as bright as the surface of a star.) However, the night sky is largely dark. Since the 1600s, astronomers and other thinkers have proposed many possible ways to resolve this paradox, of which the currently accepted standard depends upon the Big Bang theory. If the universe has existed for only a finite amount of time, as this theory holds, then only the light of finitely many stars has had a chance to reach us yet, and the paradox breaks down. Alternatively, if the universe is expanding and distant stars are receding from us (also a key prediction of the theory), then their light is redshifted which diminishes their brightness, again resolving the paradox. Either effect alone would resolve the paradox, but according to the Big Bang theory, both effects contribute (the finite duration of the Universe's history being usually judged the more important of the two). The darkness of the night sky, then, provides confirmation for the Big Bang.
While this redshift of distant galaxies closely resembles what would be seen if distant galaxies simply had recessional velocities, in general relativity stretching of spacetime is different from the physical movement of the source. These galaxies are not believed to be receding; instead, the intervening space is believed to be stretching, which is subtly different. Nevertheless, astronomers (especially professional ones) sometimes refer to "recession velocity" in the context of the redshifting of distant galaxies from the expansion of the Universe, even though it is only an apparent recession. More mathematically, the viewpoint that "distant galaxies are receding" and the viewpoint that "the space between galaxies is expanding" are related by changing coordinate systems. Expressing this precisely requires working with the mathematics of the Robertson-Walker metric.
Relativistic effects
In a third class of vacuum redshifts, the frequency of the source is lowered by relativistic effects. One possibility is the time dilation of special relativity, which introduces the Lorentz factor into the classical Doppler formula,
which was first observed in a 1938 experiment performed by Herbert E. Ives and G.R. Stilwell, called the Ives-Stilwell experiment . For the special case that the source is moving at right angles to the detector, the relativistic redshift is known as the transverse redshift.

In the theory of general relativity, there is also time dilation within a gravitational well. This is known as the gravitational redshift or Einstein Shift. The effect is very small but measurable on Earth using the Mossbauer effect and was first observed in the Pound-Rebka experiment . However, it is significant near a black hole, and as an object approaches the event horizon, the red shift becomes infinite. It is also the dominant cause of large angular-scale temperature fluctuations in the cosmic microwave background radiation (see Sachs-Wolfe effect). In the 1970s, science historians discovered a letter dated 1784 from John Michell, a natural philosopher and geologist, to scientist Henry Cavendish, in which he considers the effect of a heavenly object massive enough to prevent light from escaping (see black hole), and using a prism to measure the gravitational weakening of starlight due to the surface gravity of the source. This letter has been considered to be the first prediction of gravitational redshift .
"Reddening" due to scattering
The scattering of electromagnetic radiation whether from charged elementary particles, from particulates, or from fluctuations in a dielectric medium can cause shifts in the wavelength and frequency of the waves which are sometimes referred to as "redshifts" and "blueshifts". The electromagnetic interaction of the photons with intervening matter distinguishes scattering "redshift" from the vacuum effects discussed above.
In many circumstances scattering causes the radiation to redden because entropy results in the predominance of many low energy photons over few high energy ones (while conserving total energy). Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated z is generally a function of wavelength. Furthermore, scattering from random media generally occurs at many angles, and z is also a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of spectral lines as well.
In interstellar astronomy, visible spectra can appear redder due to scattering processes in a phenomenon referred to as interstellar reddening — the same effect that causes the atmospheric reddening of the sun seen in the sunrise or sunset and causes the rest of the sky to have a blue color. This phenomenon is distinct from redshifting because the spectroscopic lines are not shifted to other wavelengths in reddened objects and there is an additional dimming and distortion associated with the phenomenon due to photons being scattered in and out of the line of sight.
For a list of scattering processes, see Scattering.
Observations in astronomy
The redshift observed in astronomy can be measured because the emission and absorption spectra for atoms are distinctive and well known, calibrated from spectroscopic experiments in laboratories on Earth. When the redshift of various absorption and emission lines from a single astronomical object is measured, z is found to be remarkably constant. (See Is the fine structure constant really constant?) Furthermore, distant objects are not blurred, and the lines are not broadened more than can be explained by thermal or mechanical motion of the source. For these reasons and others, the consensus among astronomers is that the redshifts they observe are due to some combination of the three established forms of Doppler-like redshifts. Alternative hypotheses (for example, tired light and other suggestions from nonstandard cosmologies) are not generally considered plausible.
Local observations
In nearby objects (within our Milky Way galaxy) observed redshifts are almost always related to the line of sight velocities associated with the objects being observed. Observations of such redshifts and blueshifts have enabled astronomers to measure velocities and parametrize the masses of the orbiting stars in spectroscopic binaries, a method first employed in 1868 by British astronomer William Huggins. Similarly, small redshifts and blueshifts detected in the spectroscopic measurements of individual stars are one way astronomers have been able to diagnose and measure the presence and characteristics of planetary systems around other stars. Measurements of redshifts to fine detail are also used in helioseismology to determine the precise movements of the photosphere of the Sun. Redshifts have also been used to measure the velocity of gas of interstellar clouds, the rotation of galaxies, and the dynamics of accretion onto neutron stars and black holes which exhibit both Doppler and gravitational redshifts. Additionally, the temperatures of various emitting and absorbing objects can be obtained by measuring Doppler broadening — effectively redshifts and blueshifts over a single emission or absorption line. By measuring the broadening and shifts of the 21-centimeter hydrogen line in different directions, astronomers have been able to measure the recessional velocities of interstellar gas, which in turn reveals the rotation curve of our Milky Way. Similar measurements have also been performed on other galaxies, such as Andromeda. As a diagnostic tool, measuring redshifts is one of the most important spectroscopic measurements made in astronomy.
Extragalactic observations
| Part of a series on | ||||
| Physical cosmology | ||||
|---|---|---|---|---|
 | ||||
Early universe
|
||||
| Expansion · Future | ||||
Components · Structure
|
||||
| Experiments | ||||
| Scientists | ||||
| Subject history | ||||
The most distant objects exhibit larger redshifts corresponding to the Hubble flow of the universe. The largest observed redshift, corresponding to the greatest distance and furthest back in time, is that of the cosmic microwave background radiation; the numerical value of its redshift is about z = 1089 (z = 0 corresponds to present time), and it shows the state of the Universe about 13.7 billion years ago, and 379,000 years after the initial moments of the Big Bang.
The luminous point-like cores of active galactic nuclei (quasars) were the first "high-redshift" () objects discovered before the improvement of telescopes allowed for the discovery of extended-source high-redshift galaxies. Currently, the highest measured quasar redshift is , with the highest confirmed galaxy redshift being while as-yet unconfirmed reports from a gravitational lens observed in a distant galaxy cluster may indicate a galaxy with a redshift of .
For galaxies more distant than the Local Group and the nearby Virgo Cluster, but within a thousand megaparsecs or so, the redshift is approximately proportional to the galaxy's distance. This correlation was first observed by Edwin Hubble and has come to be known as Hubble's law. Vesto Slipher was the first to discover galactic redshifts, in about the year 1912, while Hubble correlated Slipher's measurements with distances he measured by other means to formulate his Law. In the widely accepted cosmological model based on general relativity, redshift is mainly a result of the expansion of space: this means that the farther away a galaxy is from us, the more the space has expanded in the time since the light left that galaxy, so the more the light has been stretched, the more redshifted the light is, and so the faster it appears to be moving away from us. Hubble's law follows in part from the Copernican principle. Measuring the redshift is often easier than more direct distance measurements, so redshift is sometimes in practice converted to a crude distance measurement using Hubble's law.
Gravitational interactions of galaxies with each other and clusters cause a significant scatter in the normal plot of the Hubble diagram. The peculiar velocities associated with galaxies superimpose a rough trace of the mass of virialized objects in the universe. This effect leads to such phenomena as nearby galaxies (such as the Andromeda Galaxy) exhibiting blueshifts as we fall towards a common barycenter, and redshift maps of clusters showing a Finger of God effect due to the spread of peculiar velocities in a roughly spherical distribution. This added component gives cosmologists a chance to measure the masses of objects independent of the mass to light ratio (the ratio of a galaxy's mass in solar masses to its brightness in solar luminosities), an important tool for measuring dark matter.
For more distant galaxies, the relationship between current distance and observed redshift becomes more complex. When one sees a distant galaxy, one is seeing the galaxy as it was sometime in the past, when the expansion rate of the Universe was different from what it is now. At these early times, we expect differences in the expansion rate for at least two reasons:
- The gravitational attraction between galaxies has been acting to slow down the expansion of the Universe since then.
- The possible existence of a cosmological constant may be changing the expansion rate of the Universe.
Recent observations have suggested the expansion of the Universe is not slowing down, as expected from the first point, but accelerating (see accelerating universe). It is widely, though not quite universally, believed that this is because there is a form of the cosmological constant due to a scalar field dubbed dark energy. Such a cosmological constant also implies that the ultimate fate of the Universe is not a Big Crunch, but instead will continue to exist foreseeably (though most physical processes within the Universe will still come to an eventual end).
The expanding Universe is a central prediction of the Big Bang theory. If extrapolated back in time, the theory predicts a "singularity", a point in time when the Universe had infinite density. The theory of general relativity, on which the Big Bang theory is based, breaks down at this point. It is believed that a yet unknown theory of quantum gravity would take over before the density becomes infinite.
Redshift surveys
Main article: redshift survey
With the advent of automated telescopes and improvements in spectroscopes, a number of collaborations have been made to map the universe in redshift space. By combining redshift with angular position data, a redshift survey maps the 3D distribution of matter within a field of the sky. These observations are used to measure properties of the large-scale structure of the universe. The Great Wall, a vast supercluster of galaxies over 500 million light-years wide, provides a dramatic example of a large-scale structure that redshift surveys can detect.
The first redshift survey was the CfA Redshift Survey, started in 1977 with the initial data collection completed in 1982. More recently, the 2dF Galaxy Redshift Survey determined the large-scale structure of one section of the Universe, measuring z-values for over 220,000 galaxies; data collection was completed in 2002, and the final data set was released 30 June 2003. (In addition to mapping large-scale patterns of galaxies, 2dF also established an upper limit on neutrino mass.) Another notable investigation, the Sloan Digital Sky Survey (SDSS), is ongoing as of 2005 and aims to obtain measurements on around 100 million objects. SDSS has recorded redshifts for galaxies as high as 0.4, and has been involved in the detection of quasars beyond z = 6. The DEEP2 Redshift Survey uses the Keck telescopes with the new "DEIMOS" spectrograph; a follow-up to the pilot program DEEP1, DEEP2 is designed to measure faint galaxies with redshifts 0.7 and above, and it is therefore planned to provide a complement to SDSS and 2dF.
See also
- Blue shift
- Fingers of God - cosmological effect causing elongation of galaxies in redshift space
- Phase shift
- Relativistic Doppler effect
- Transverse Doppler effect
References
Citations
- S. I. Chase, Olbers' Paradox, entry in the Physics FAQ; see also I. Asimov, Far as Human Eye Could See (Doubleday, 1987), ISBN 0-385-23514-3
- M. Weiss, What Causes the Hubble Redshift?, entry in the Physics FAQ (1994), available via John Baez's website
- H. Ives and G. Stilwell, An Experimental study of the rate of a moving atomic clock , J. Opt. Soc. Am. 28, 215-226 (1938)
- R. V. Pound and G. A. Rebka Jr., Apparent weight of photons, Phys. Rev. Lett. 4, 337 (1960). This paper was the first measurement.
- J. Michell, Phil. Trans. Roy. Soc., 74 (1784) 35-57.
- Fan, Xiahoui et al., A Survey of z>5.7 Quasars in the Sloan Digital Sky Survey. II. Discovery of Three Additional Quasars at z>6, The Astronomical Journal (2003), v. 125, Issue 4, pp. 1649-1659 .
- Egami, E., et al., Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218, The Astrophysical Journal (2005), v. 618, Issue 1, pp. L5-L8 .
- Pelló, R., Schaerer, D., Richard, J., Le Borgne, J.-F., & Kneib, J.P., ISAAC/VLT observations of a lensed galaxy at z = 10.0, Astronomy and Astrophysics (2004), 416, L35 .
Book references
- Carroll, Bradley W. and Dale A. Ostlie (1996). An Introduction to Modern Astrophysics. Addison-Wesley Publishing Company, Inc. ISBN 0201547309.
- Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 0521529271.
External links
- Gravitational redshift
- Ned Wright's Cosmology tutorial
- Article on redshift from SPACE.com
- Cosmic reference guide entry on redshift
- Mike Luciuk's Astronomical Redshift tutorial

 is the wavelength of electromagnetic radiation.
is the wavelength of electromagnetic radiation.

 is the frequency of electromagnetic radiation.
is the frequency of electromagnetic radiation.


 ) in the following way:
) in the following way:

 into the classical Doppler formula,
into the classical Doppler formula,

 ) objects discovered before the improvement of telescopes allowed for the discovery of extended-source high-redshift
) objects discovered before the improvement of telescopes allowed for the discovery of extended-source high-redshift  , with the highest confirmed galaxy redshift being
, with the highest confirmed galaxy redshift being  while as-yet unconfirmed reports from a
while as-yet unconfirmed reports from a  .
.