| Revision as of 19:09, 8 November 2010 editBrews ohare (talk | contribs)47,831 edits →Bloat: Guess we differ; too bad, I'd say.← Previous edit | Revision as of 06:39, 9 November 2010 edit undoDicklyon (talk | contribs)Autopatrolled, Extended confirmed users, Rollbackers477,511 edits →BloatNext edit → | ||
| Line 258: | Line 258: | ||
| :::Apparently we disagree upon one role of a WP article as being the expansion of reader awareness of the ramifications of a topic. Personally, I find this aspect to be one of the cardinal virtues of a WP article. ] (]) 19:09, 8 November 2010 (UTC) | :::Apparently we disagree upon one role of a WP article as being the expansion of reader awareness of the ramifications of a topic. Personally, I find this aspect to be one of the cardinal virtues of a WP article. ] (]) 19:09, 8 November 2010 (UTC) | ||
| :For reference, here's the removed material: | |||
| These proofs depend upon an assumption of Euclidean geometry not stated in ]<ref name=Trudeau> | |||
| {{cite book |title=The Non-Euclidean Revolution |author=Richard J. Trudeau |pages=39 '''ff'' |url=http://books.google.com/books?id=YRB4VBCLB3IC&pg=PA39 |chapter=Euclid's axioms |publisher= Birkhäuser |year=2008 |isbn=0817647821}} | |||
| </ref> that certain movements of figures do not change their geometrical properties such as the lengths of sides and interior angles, the so-called ''Euclidean motions'', which include translations and rotations of figures.<ref name=Euclidean_Motion> | |||
| See, for example: {{cite book |title=Shape analysis and classification: theory and practice |author=Luciano da Fontoura Costa, Roberto Marcondes Cesar |page=314 |url=http://books.google.com/books?id=x_wiWedtc0cC&pg=PA314 |isbn=0849334934 |year=2001 |publisher=CRC Press}} and {{cite book |title=Computational Line Geometry |author=Helmut Pottmann, Johannes Wallner |url=http://books.google.com/books?id=3Mk2JIJKsGwC&pg=PA60 |page=60 |isbn=3642040179 |year=2010 |publisher=Springer}} The ''group of motions'' underlie the metric notions of geometry. See {{cite book |title=Elementary Mathematics from an Advanced Standpoint: Geometry |author=Félix Klein |url=http://books.google.com/books?id=fj-ryrSBuxAC&pg=PA167 |page=167 |isbn=0486434818 |publisher=Courier Dover |year=2004 |edition=Reprint of 1939 Macmillan Company}} </ref> | |||
| {{reflist}} | |||
| :I've checked the refs, but don't find support for Dr. Brews's assertion that "These proofs depend upon an assumption of Euclidean geometry not stated in Euclid's fundamental axioms." They appear rather to affirm that congruence comes directly out of Euclid. I'd need to see a source to think other than that this is yet another Brews idiosyncratic interpretation. Of course, I may have just missed it, in which case he can simply point it out, and then say what indicates that it should be discussed in the context of the Pythagorean theorem. ] (]) 06:39, 9 November 2010 (UTC) | |||
Revision as of 06:39, 9 November 2010
| Pythagorean theorem is a former featured article. Please see the links under Article milestones below for its original nomination page (for older articles, check the nomination archive) and why it was removed. | ||||||||||||||||||||||
| Pythagorean theorem has been listed as one of the Mathematics good articles under the good article criteria. If you can improve it further, please do so. If it no longer meets these criteria, you can reassess it. | ||||||||||||||||||||||
| ||||||||||||||||||||||
| This article has not yet been rated on Misplaced Pages's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
| |||||||||||
| This article was reviewed by Nature on December 14, 2005. Comments: It was found to have 1 error; this error has been fixed. For more information about external reviews of Misplaced Pages articles and about this review in particular, see this page. |
|
Archives |
|
This page has archives. Sections older than 60 days may be automatically archived by Lowercase sigmabot III when more than 4 sections are present. |
Converse?
The first statement in the converse section is not quite right:
For any three positive numbers a, b, and c such that , there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.
The first part of this statement is not the converse to the Pythagorean theorem. It actually follows directly from the Pythagorean theorem. Simply take a right triangle with side lengths a and b. By Pythagoras' theorem, the hypotenuse must be c. Showing that any triangle with side lengths a,b, and c satisfying has a right angle is the converse. This is stated a few lines down, but I wonder why the section on the converse does not start with this. I will change if no one objects. Paul Laroque (talk) 03:02, 28 September 2010 (UTC)
- You have a point and the cited reference doesn't support the addition either. Euclid's version of the converse is noteworthy simply because it's Euclid's, and another one using modern notation is useful, but it seems a bit redundant to have three versions of it.--RDBury (talk) 08:27, 28 September 2010 (UTC)
Dimensional analysis
I have added a dimensional proof of the Pythagorean theorem. I believe it, at least for me (a physicist), much more convincing than all those complicated triangle rearrangements which are used in most other proofs. Unfortunately, though I have given an academic reference, I don't know who originally proposed it. If someone knows, please add the reference.--GianniG46 (talk) 12:50, 13 October 2010 (UTC)
- The proof is very interesting, but I'm afraid that it isn't actually a proof. The issue is that you have assumed that the form of the area is where f is dimensionless. Ignoring the question of whether dimensional analysis is a valid proof technique at all (which I would say it is not), the assumption about the form of the area is far from obvious. It would be equally possible for the area to be of the form where g has units of length (for example, if g includes some constant that has units of length). It would even be possible, in principle, for the area to be of the form where h has units of (length). The deeper issue is that dimensional analysis is not a valid proof technique, but even if it was there is no reason that the area would need to be in the form specified in that argument. In general all that can be said is that the area can be written as some function of c, α, and β – the form of the function cannot be known ahead of time. — Carl (CBM · talk) 14:34, 13 October 2010 (UTC)
- I don't quite understand why it's called "dimensional analysis", but it is a general property of the n-dimensional Lebesgue (or Hausdorff) measure that if A and B are similar objects with coefficient of similarity r, then λB = rλA. Triangles with the same angles are similar, and the coefficient is the ratio of their longest sides, which indeed implies that the area is cf(α,β) for some f.—Emil J. 14:51, 13 October 2010 (UTC)
- Yes; I was commenting only on the proof as it was written, which seemed to claim that the form of the area function follows solely from its units.
- I don't quite understand why it's called "dimensional analysis", but it is a general property of the n-dimensional Lebesgue (or Hausdorff) measure that if A and B are similar objects with coefficient of similarity r, then λB = rλA. Triangles with the same angles are similar, and the coefficient is the ratio of their longest sides, which indeed implies that the area is cf(α,β) for some f.—Emil J. 14:51, 13 October 2010 (UTC)
- If we rewrite the proof in terms of similarity, it has the same essence as the "similarity proof" that the article already includes. I think it would be nice to expand out that proof sketch to something more detailed, since this is a very pretty proof. I'll see what I can do. — Carl (CBM · talk) 17:03, 13 October 2010 (UTC)
- So, now the proof is correct, provided that you change the words "dimensions of a length squared" with "scales by a factor of s^2". Now I ask: this is the same concept or not? And, if the question was only the language, it was not possible to correct my text, rather than deleting it, keep its concepts, and rewrite it again? I think it is incorrect: a) to delete without a previous discussion a contribution with citations and not obviously wrong . b) to use the material to write another contribution instead of trying to amend the original contribution. --GianniG46 (talk) 20:45, 13 October 2010 (UTC)
- I thought that, modulo the issue with dimensional analysis, the idea behind the proof was nice. At first, I was somewhat blinded by the dimensional analysis issue and didn't I realize that the text could be transformed into a better proof of the "similarity" method that was already sketched obliquely in the article. The invocation of dimensional analysis was a red herring for me.
- Once EmilJ pointed out how the proof method could be salvaged, I went right back and did that. I apologize for not taking the most direct route to the current state of the article. However, I think that the outcome is good so far: we have a more clear version of what you wrote, merged with a previously less clear section on similarity. — Carl (CBM · talk) 21:09, 13 October 2010 (UTC)
This proof is not as well described as it might be. For example, when the hypotenuse is scaled by c, it is assumed, but not pointed out, that all the angles (not just the right angle) are held fixed, and that this implies the other two sides are also scaled in the same proportion. That is tantamount to a theorem that the sine of an angle is a function of the angle only, and not the lengths of the sides, an observation tantamount to Pythagoras' theorem, and the reason the proof works. This article in general is unclear about the difference between equivalence of statements and proofs strictly based upon the fundamental axioms themselves. That failure unfortunately undermines the notion of a deductive system. Brews ohare (talk) 17:31, 14 October 2010 (UTC)
Proof by area vs. proof by rotation
Perhaps the interested parties can bring this discussion to the talk page instead of brewing an edit war? Orange Suede Sofa (talk) 18:13, 3 November 2010 (UTC)
- I don't think we're anywhere near an edit war, but for the record here's my reason for restoring Hgilbert's change, expanded from the edit summary. The proof has little to do with rotation. The only things that need to be rotated are the triangles, but that is true of many of the proofs that involve triangles, such as the one immediately above. The square does not need to be rotated as it is clear it is a square, with sides length c and right angled corners, even inclined.--JohnBlackburnedeeds 18:31, 3 November 2010 (UTC)
- FWIW, I agree with your reasoning.—Emil J. 18:41, 3 November 2010 (UTC)
Proof by rotation

It seems that this example can be misinterpreted, so I've tried to rewrite this section to be clearer.
The top square in this figure is a rotated version of the lower square. The angle of rotation can be expressed as one or the other of the two acute angles of the right triangles inserted in the top figure.
The area of the square is not changed by its rotation, so the area computed from the top square is the same as that of the bottom square. It is of interest to point out that the rotational invariance of area is a factor in this proof. Brews ohare (talk) 18:46, 3 November 2010 (UTC)
- As noted above the proof has nothing to do with such rotation, as in it works fine without rotating the square. The source also says nothing about rotating the square, just that the triangles are rotated as in many of the other proofs, so the rotation of the square is something added by an editor which is unnecessary for the proof.--JohnBlackburnedeeds 19:00, 3 November 2010 (UTC)
- John: The proof that doesn't involve rotation, does not involve rotation. As such it is a repetition of proofs by rearrangement already in this article, and can be deleted altogether. Its only interest here is the rotational connection. Brews ohare (talk) 19:22, 3 November 2010 (UTC)
- I'm not sure what you mean by your first sentence. I don't see any need to remove it: it's sourced and is one of two algebraic proofs, i.e. one where the areas of the figures are derived and expressed algebraically, which then gives the result. The two proofs are similar but different both in the figures used and the algebra.--JohnBlackburnedeeds 19:41, 3 November 2010 (UTC)
- John: The proof that doesn't involve rotation, does not involve rotation. As such it is a repetition of proofs by rearrangement already in this article, and can be deleted altogether. Its only interest here is the rotational connection. Brews ohare (talk) 19:22, 3 November 2010 (UTC)
John, as you are probably aware, Euclidean geometry tacitly assumes that translations and rotations do not alter the geometric properties of figures, such as their areas. I believe the concept is Euclidean congruence transformations or Euclidean motions.
In this particular example, the top panel is a square of area a + b that is a rotation of the square in the lower panel of area c. Because rotation doesn't alter the area of a figure, a + b = c.
Now you may argue that this isn't the only way to look at it, but I'd hope you would agree that it is a valid way to look at it. More than that, it is an interesting way to look at because it invokes a different aspect of Euclidean geometry not before discussed in this article that leads to Pythagoras' theorem.
So I have added this view to the discussion. Brews ohare (talk) 12:17, 4 November 2010 (UTC)
- I have removed this "interesting perspective" since it is unsourced: giving two sourced statements and drawing a conclusion from them is not allowed per wp:SYNTH in wp:NOR. DVdm (talk) 12:28, 4 November 2010 (UTC)
DVdm: You have mischaracterized the example. It consists of the following statements:
1. The top panel is a rotation of the square in the lower panel. I believe that is an obvious statement that you would not disagree with and would not require a source for.
2. The invariance of figures under Euclidean motions is attested to by the sources provided. In any event, such sourcing is overkill inasmuch as Euclid made this assumption centuries ago without comment. The main purpose of the sources is to expand the topic for a reader that might find a more general approach of interest.
3. The conclusion is hardly WP:SYN since it amounts to A = c and A = a + b so c = a + b. Simple syllogism is allowed by WP:SYN.
On the basis that your reversion is incorrectly based I have replaced the observation. Brews ohare (talk) 12:40, 4 November 2010 (UTC)
- You don't need to explain things here. You have given two sourced statements and have drawn an unsourced conclusion. That is a schoolbook example of wp:SYNTH. Please remove that entry again. DVdm (talk) 12:46, 4 November 2010 (UTC)
- Pardon me, but can you identify the unsourced conclusion? Is it that the two areas are equal? Is it that rotations leave area unaltered? What is it that you find to be an unwarranted conclusion, please? Brews ohare (talk) 12:56, 4 November 2010 (UTC)
- Referring to this edit:
- Sourced statement #1: "... observing that the top square of area b^2 + a^2 is simply a rotation of the lower square of area c^2"
- Sourced statement #2: "A tacit assumption of Euclidean geometry is that geometric properties of figures (area being one) are not changed by translations and rotations."
- Unsourced conclusion: "As a consequence of this invariance under rotations, b^2 + a^2 = c^2"
- A schoolbook example of wp:SYNTH. DVdm (talk) 13:21, 4 November 2010 (UTC)
- DVdm: No it is isn't. It's a Routine math operation, an obvious use of a common syllogism that no-one in their right mind would challenge. Brews ohare (talk) 13:35, 4 November 2010 (UTC)
- ==> "... routine mathematical calculations, such as adding numbers, converting units, or calculating a person's age ...". They don't say anything a logical deductions like in "Do not combine material from multiple sources to reach or imply a conclusion not explicitly stated by any of the sources. If one reliable source says A, and another reliable source says B, do not join A and B together to imply a conclusion C that is not mentioned by either of the sources." If you don't like this, then feel free to file for policy change at, perhaps, Wikipedia_talk:No_original_research. DVdm (talk) 15:07, 4 November 2010 (UTC)
- DVdm: No it is isn't. It's a Routine math operation, an obvious use of a common syllogism that no-one in their right mind would challenge. Brews ohare (talk) 13:35, 4 November 2010 (UTC)
- Referring to this edit:
- Pardon me, but can you identify the unsourced conclusion? Is it that the two areas are equal? Is it that rotations leave area unaltered? What is it that you find to be an unwarranted conclusion, please? Brews ohare (talk) 12:56, 4 November 2010 (UTC)
- The lower square is irrelevant. The upper square is a square with side c and so area c, there's no need to rotate it to see this. There are now four editors who disagree with your irrelevant additions or rewriting of this proof, so please stop editing against consensus.--JohnBlackburnedeeds 12:48, 4 November 2010 (UTC)
- John: No argument from me that you can establish the result differently. The point is that this example also illustrates a different point of view, invariance under rotations. You do not suggest that this argument is mistaken, do you? The "four editors" haven't addressed this issue; the two editors that have are you and DVdm. Brews ohare (talk) 12:56, 4 November 2010 (UTC)
- Four being User:Hgilbert who fixed the erroneous association with rotation, I who restored his improvements after you reverted them User:EmilJ who agreed with my reasons for doing so and User:DVdm who also reverted your unnecessary changes. We already have a clear consensus on this, there's no need to waste other editors' time with it. Please remove the RfC.--JohnBlackburnedeeds 14:03, 4 November 2010 (UTC)
- User:Hgilbert and User:EmilJ simply agreed that the algebraic version followed the source given. There is no statement by anyone, except possibly yourself, that the connection to rotation is "erroneous". Is that really your considered opinion as a mathematician?? I'll let other editors comment directly upon the matter as actually proposed through the RfC. Brews ohare (talk) 14:22, 4 November 2010 (UTC)
- I didn't care about any sources. The problem is that the rotation of the outer square is pointless and misleading, and misses the actual reason why the argument works.—Emil J. 14:29, 4 November 2010 (UTC)
- EmilJ: I understand that the argument already presented works. That doesn't mean another argument is false, pointless, or misleading; it is just different. An argument based upon rotation may be strange to you, but it is as valid as the first argument. Rotational invariance is a well recognized concept within Euclidean geometry, and pointing out its connection here seems to me to broaden the reader's understanding and provide some new directions to think in. Brews ohare (talk) 14:45, 4 November 2010 (UTC)
- I didn't care about any sources. The problem is that the rotation of the outer square is pointless and misleading, and misses the actual reason why the argument works.—Emil J. 14:29, 4 November 2010 (UTC)
- User:Hgilbert and User:EmilJ simply agreed that the algebraic version followed the source given. There is no statement by anyone, except possibly yourself, that the connection to rotation is "erroneous". Is that really your considered opinion as a mathematician?? I'll let other editors comment directly upon the matter as actually proposed through the RfC. Brews ohare (talk) 14:22, 4 November 2010 (UTC)
- Four being User:Hgilbert who fixed the erroneous association with rotation, I who restored his improvements after you reverted them User:EmilJ who agreed with my reasons for doing so and User:DVdm who also reverted your unnecessary changes. We already have a clear consensus on this, there's no need to waste other editors' time with it. Please remove the RfC.--JohnBlackburnedeeds 14:03, 4 November 2010 (UTC)
- John: No argument from me that you can establish the result differently. The point is that this example also illustrates a different point of view, invariance under rotations. You do not suggest that this argument is mistaken, do you? The "four editors" haven't addressed this issue; the two editors that have are you and DVdm. Brews ohare (talk) 12:56, 4 November 2010 (UTC)
I've fixed one aspect of it, which was the confusing diagram with the redundant second square. I've replaced this with a simpler diagram which only has the inclined square, along with a copy of one of the triangles which it's easier to label the sides of. The diagram now matches the text and proof much better. As a bonus it is an SVG image, to make it easier for editors to improve or make other use of.--JohnBlackburnedeeds 14:18, 4 November 2010 (UTC)
- That is not a "fix", John, it is an interruption of an RfC to make its assessment more difficult by altering the context within which it is to be judged and prejudice the outcome. Brews ohare (talk) 14:22, 4 November 2010 (UTC)
- As noted the RfC is unnecessary as there is already clear consensus, there is nothing to stop editors improving the article while one is in progress, and the old image is still below for editors to consider. The image needed replacing anyway: the symbols "a", "b" and "c" were not italicised as they should be, had a couple of other errors, and was in PNG which makes it impossible for other editors to improve.--JohnBlackburnedeeds 14:33, 4 November 2010 (UTC)
RfC
|
It is proposed that the discussion of an example in Pythagorean theorem#Proof by areas be extended to include an alternative proof illustrating a role for rotation. Please comment upon the interest of this addition to readers, and whether you regard the discussion to be a violation of WP:SYN. The paragraph is to be placed below the algebraic discussion already present. The addition is appended below. Brews ohare (talk) 13:36, 4 November 2010 (UTC)
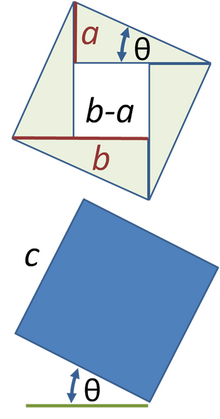
- An interesting perspective upon this example is provided by observing that the top square already established to have an area b + a is simply a rotation of the lower square of area c. A tacit assumption of Euclidean geometry is that geometric properties of figures (area being one) are not changed by translations and rotations. As a consequence of this invariance under rotations, b + a = c.
- References & notes
- The angle of rotation of the square in the lower panel of this example is the same as the smaller acute angle of the four right triangles in the upper panel.
- The general topic is that of Euclidean motions; see, for example: Luciano da Fontoura Costa, Roberto Marcondes Cesar (2001). Shape analysis and classification: theory and practice. CRC Press. p. 314. ISBN 0849334934. and Helmut Pottmann, Johannes Wallner (2010). Computational Line Geometry. Springer. p. 60. ISBN 3642040179.
Comments
Please add your comments below with a leading *.
- Include: The example provides a simple and intuitive proof of the Pythagorean theorem that uses the interesting property of invariance of geometrical properties under Euclidean motions. The proposed addition is a useful supplement to the preceding algebraic treatment because it ties into this topic of invariance. There is nothing here that violates WP:SYN. Brews ohare (talk) 13:36, 4 November 2010 (UTC)
- This approach is the "active" version of the "passive" version already presented in the article: in this "active" version the observer rotates the square, while in the "passive" version the observer rotates with the square. Brews ohare (talk) 11:32, 5 November 2010 (UTC)
- I think there are too many proofs in that section already. Also, I don't think that it's necessary to emphasize Euclidean geometry more than it is already emphasized. — Carl (CBM · talk) 14:00, 4 November 2010 (UTC)
- CBM: Somewhere in the article it says there are more proofs for this theorem than almost any other. The choice of proofs here is selective, based upon (i) historical importance (ii) unusual clarity or (iii) variety of approach, that is, introducing some connections that are a bit unusual. It is on this last basis that I've made this suggestion to connect the Pythagorean theorem to a proof by rotational invariance, which strikes me as bringing out a different aspect of the theorem that might broaden the reader's perspective and lead them in some unexpected directions. That's the value of the thing, it's not (hopefully) just "another proof". Brews ohare (talk) 15:16, 4 November 2010 (UTC)
- There are other proofs that mention similarity (of which rotational invariance is just a special case), and other proofs that do dissections of the square, already in the article. I don't think the proof "by areas" is much different than the two proofs immediately above it. — Carl (CBM · talk) 19:52, 4 November 2010 (UTC)
- Reject per "Do not combine material from multiple sources to reach or imply a conclusion not explicitly stated by any of the sources. If one reliable source says A, and another reliable source says B, do not join A and B together to imply a conclusion C that is not mentioned by either of the sources." DVdm (talk) 15:10, 4 November 2010 (UTC)
- If a math argument states A = c and A = a + b & therefore the conclusion is that c = a + b, calling this routine math operation a violation of WP:SYN is ridiculous. Brews ohare (talk) 15:21, 4 November 2010 (UTC)
- Don't include. The rotation is completely irrelevant both to the theorem and to its proof, and it makes it much more difficult to see that the two squares have the same side length (instead, one is led to the erroneous conclusion that the lower square has side length b). —David Eppstein (talk) 15:22, 4 November 2010 (UTC)
- The lower square side length is labeled c in the diagram, so confusion should be avoidable. As this proof is intended to be a proof using the concept of rotational invariance, evidently rotational invariance is not irrelevant to such a proof. It looks like what you mean is that rotational invariance is not the method used in the prior proof, already in the article, but that is not in dispute here. Brews ohare (talk) 15:40, 4 November 2010 (UTC)
- Please don't try to tell me what I see or don't see with my own eyes. Yes, obviously it's labeled c. Nevertheless it took me a long time to realize that the side length is not b. And I see nothing in the illustration that involves rotation in any necessary way. I should add that responding to all negative comments as you seem to be doing by repeating your same arguments over again comes across as somewhat tendentious. —David Eppstein (talk) 15:53, 4 November 2010 (UTC)
- David: I'm sorry you see my pointing out a label as somehow an insult; that wasn't my intention at all. Maybe the illustration is imperfect. The imperfections of the diagram have nothing to do with the argument, however, and to say that an argument based upon rotational invariance is not necessarily connected to rotation simply doesn't compute. Rotation is exactly what this particular proof involves. Aren't you saying the proof already presented in the article doesn't require rotation? That is not at issue. What do you mean? Brews ohare (talk) 16:08, 4 November 2010 (UTC)
- I believe that it only uses right-angle rotations and translations. The irrational rotation shown in the figure is an irrelevant distraction. There is no need to start with the cxc square being axis-aligned, nor is there any need to think about or depict the Cartesian coordinates of anything. —David Eppstein (talk) 16:19, 4 November 2010 (UTC)
- David: I'm sorry you see my pointing out a label as somehow an insult; that wasn't my intention at all. Maybe the illustration is imperfect. The imperfections of the diagram have nothing to do with the argument, however, and to say that an argument based upon rotational invariance is not necessarily connected to rotation simply doesn't compute. Rotation is exactly what this particular proof involves. Aren't you saying the proof already presented in the article doesn't require rotation? That is not at issue. What do you mean? Brews ohare (talk) 16:08, 4 November 2010 (UTC)
- David: I'd like to open this conversation up a little, and frame matters anew.
- Please don't try to tell me what I see or don't see with my own eyes. Yes, obviously it's labeled c. Nevertheless it took me a long time to realize that the side length is not b. And I see nothing in the illustration that involves rotation in any necessary way. I should add that responding to all negative comments as you seem to be doing by repeating your same arguments over again comes across as somewhat tendentious. —David Eppstein (talk) 15:53, 4 November 2010 (UTC)

- Suppose we start with a square of side c and area A = c and rotate it about a vertical axis through an angle θ. I'd assume that you'd agree that the area of the square is unaffected according to the notion of Euclidean motions. Then looking at the rotated square, a right triangle can be inserted with acute angle θ, and its hypotenuse along (say) the top side of the rotated square. Taking the two short sides of the right triangle as a and b, one can deduce the rotated square has area A = a + b. Then by invariance of A one finds A = a + b = c.
- Let me rewrite this for you. Suppose we start with a square of side c and area c. Then a right angle can be inserted with acute angle on its four corners. One can deduce that 'A = a + b etc. You are not assuming an axis-aligned square and axis-aligned right triangles in your version of this paragraph (and if you were I'd question your assumptions), so the "rotate it about a vertical axis" looks totally irrelevant to me: why does rotating a square make it any easier or any more difficult to insert right triangles in it? It doesn't. You are locked into some Cartesian mindset that has nothing to do with the actual geometry. —David Eppstein (talk) 18:41, 4 November 2010 (UTC)
- Hi David: A Cartesian mindset is not what I am using. It appears to boil down to whether the observer rotates with the square so it appears fixed in orientation and examines various possible triangle orientations within the square, or the observer rotates the square and examines its orientation using various triangles that maintain the alignment of their shorter sides. Does the observer rotate the square or rotate with the square? WP seems to be having some trouble, but you can see the new figure by clicking on the small pair of overlaid rectangles in the display case. Brews ohare (talk) 19:48, 4 November 2010 (UTC)
- So you are starting out with a square that makes an angle of 13.457° to the x-axis, right? And rotating it by tan(b/a) so that you can put the triangles into it, you end up with a square that makes an angle of 13.457°+tan(b/a) to the axis. But what's the point? Why not just start with the square of the orientation you want, rather than starting with a different square and rotating it? It seems to me a totally unnecessary step. Ok, you didn't say the 13.457° part; instead you seem to be assuming that it starts out axis-parallel. But why? What is the point of starting with that orientation? —David Eppstein (talk) 20:46, 4 November 2010 (UTC)
- Hi David: A Cartesian mindset is not what I am using. It appears to boil down to whether the observer rotates with the square so it appears fixed in orientation and examines various possible triangle orientations within the square, or the observer rotates the square and examines its orientation using various triangles that maintain the alignment of their shorter sides. Does the observer rotate the square or rotate with the square? WP seems to be having some trouble, but you can see the new figure by clicking on the small pair of overlaid rectangles in the display case. Brews ohare (talk) 19:48, 4 November 2010 (UTC)
- Let me rewrite this for you. Suppose we start with a square of side c and area c. Then a right angle can be inserted with acute angle on its four corners. One can deduce that 'A = a + b etc. You are not assuming an axis-aligned square and axis-aligned right triangles in your version of this paragraph (and if you were I'd question your assumptions), so the "rotate it about a vertical axis" looks totally irrelevant to me: why does rotating a square make it any easier or any more difficult to insert right triangles in it? It doesn't. You are locked into some Cartesian mindset that has nothing to do with the actual geometry. —David Eppstein (talk) 18:41, 4 November 2010 (UTC)
- Suppose we start with a square of side c and area A = c and rotate it about a vertical axis through an angle θ. I'd assume that you'd agree that the area of the square is unaffected according to the notion of Euclidean motions. Then looking at the rotated square, a right triangle can be inserted with acute angle θ, and its hypotenuse along (say) the top side of the rotated square. Taking the two short sides of the right triangle as a and b, one can deduce the rotated square has area A = a + b. Then by invariance of A one finds A = a + b = c.

- Hi David: At last the WP image problem has been fixed and you can see the figure. I start out with a square of area A = c and rotate it by θ = 13.457° (your example). Then this orientation is described using the sides a and b of an inserted right triangle, leading to the result A = a + b. I think we're both in accord to this point. Now, you say the rotation is unnecessary, just do the math and find Pythagoras' theorem. I agree that will work and that is the explanation given in the article right now. However, where we can't seem to get traction is that one can simply say "Hey, area isn't affected by rotation. We see that the original area was A = c so the new area A = a + b is the same.
- To me all this was immediately transparent. It also brought up the topic of Euclidean motions, which I thought was a nice segue. However, it now appears that the proof based upon just inserting triangles into a fixed square is so powerful a fixation on the mind that it takes an earthquake to think about the problem as rotating the square instead. It's like those pictures that you have to look at for minutes before it suddenly clicks that the vase are also can be seen as two people looking at each other. Brews ohare (talk) 22:30, 4 November 2010 (UTC)
- Brews, none of us has a "fixation" as you suggest. The proof that's there is complete, matches the source, and needs none of your additions about rotations. All you have achieved with this RfC is you've wasted another two editors time trying to explain to you that a very elementary proof is correct. Now there are six editors that have in one way or another agreed that additions on rotation are unneeded. Please accept that as clear consensus and stop repeating the same flawed arguments.--JohnBlackburnedeeds 22:48, 4 November 2010 (UTC)
- Blackburne: I agree with you as I have always done that the proof in the article is "complete, matches the source, and needs none of your additions about rotations". That observation of yours also is beside the point. What is being discussed is a different approach. You can present your opinion about the value of this addition, but you are mistaken to impugn its accuracy and to suggest that this discussion is about the validity of the other method. Brews ohare (talk) 23:10, 4 November 2010 (UTC)
- Brews, none of us has a "fixation" as you suggest. The proof that's there is complete, matches the source, and needs none of your additions about rotations. All you have achieved with this RfC is you've wasted another two editors time trying to explain to you that a very elementary proof is correct. Now there are six editors that have in one way or another agreed that additions on rotation are unneeded. Please accept that as clear consensus and stop repeating the same flawed arguments.--JohnBlackburnedeeds 22:48, 4 November 2010 (UTC)
- I don't understand why anything has to be rotated. Any square of side length c has area c regardless of orientation. Similarly the area of a triangle is not affected by rotation or translating it. — Carl (CBM · talk) 19:55, 4 November 2010 (UTC)
- Carl: That is the very fact used to prove the theorem, which is a proof based upon rotational invariance of area. Brews ohare (talk) 20:04, 4 November 2010 (UTC)
- So why not just compute the area without rotating the square? What's the point of doing any rotation whatsoever? Nothing requires the square to be in any particular orientation. — Carl (CBM · talk) 23:17, 4 November 2010 (UTC)
- Carl: That is the very fact used to prove the theorem, which is a proof based upon rotational invariance of area. Brews ohare (talk) 20:04, 4 November 2010 (UTC)
- Now, one can arrive at the relation A = a + b = c directly without invoking rotational invariance, but one can also do it this way using rotational invariance. The fact that rotational invariance is not required by one proof and is required by the other is not an argument for or against either method, would you agree?
- The question of the right diagram to illustrate this matter is a separate issue worth discussing by itself. Brews ohare (talk) 16:43, 4 November 2010 (UTC)
- Suppose we start with a square of side c and area A = c. Let us also take k, l, m, and n such that k + l = m. I'd assume that you'd agree that Fermat's Last Theorem has been proven by Wiles, hence n ≤ 2. Then looking at the original square, a right triangle can be inserted with acute angle θ, and its hypotenuse along (say) the top side of the square. Taking the two short sides of the right triangle as a and b, one can deduce the square has area A = a + b. Then one finds c = A = a + b.
- The question of the right diagram to illustrate this matter is a separate issue worth discussing by itself. Brews ohare (talk) 16:43, 4 November 2010 (UTC)
- Now, one can arrive at the relation A = a + b = c directly without invoking Fermat's Last Theorem, but one can also do it this way using Fermat's Last Theorem. The fact that Fermat's Last Theorem is not required by one proof and is required by the other is not an argument for or against either method, would you agree?—Emil J. 16:48, 4 November 2010 (UTC)
- EmilJ: I understand that you are trying to make it appear that rotational invariance is irrelevant to the argument, but this fact it is used to show the areas are the same. If you want to attempt this with Fermat's last theorem, you'll need to lay a basis. Brews ohare (talk) 17:54, 4 November 2010 (UTC)
- There is no need to show "the areas are the same" as there's no need for the second square. The top square in your diagram is a square with side c so area c, as required. Rotating it achieves nothing and shows nothing.--JohnBlackburnedeeds 17:59, 4 November 2010 (UTC)
- EmilJ: I understand that you are trying to make it appear that rotational invariance is irrelevant to the argument, but this fact it is used to show the areas are the same. If you want to attempt this with Fermat's last theorem, you'll need to lay a basis. Brews ohare (talk) 17:54, 4 November 2010 (UTC)
- Now, one can arrive at the relation A = a + b = c directly without invoking Fermat's Last Theorem, but one can also do it this way using Fermat's Last Theorem. The fact that Fermat's Last Theorem is not required by one proof and is required by the other is not an argument for or against either method, would you agree?—Emil J. 16:48, 4 November 2010 (UTC)
- The fact that this is being discussed here in the first place, clearly shows that we are indeed dealing with original research. This discussion should not even happen. DVdm (talk) 17:31, 4 November 2010 (UTC)
- No. Rotation is a red herring. It has nothing to do with this proof and only serves to make it more complicated. Hans Adler 20:29, 4 November 2010 (UTC)
- To everyone except Brews ohare: It seems clear to me that Brews is just repeating his talking points, not responding in any substance to our repeated questioning of the relevance of the rotation, and has nothing additional to add. I don't see the point of continuing the conversation any longer. At this point I think we should either just stop responding to his responses to... and revert additional attempts to add the irrelevant rotation without further discussion, or possibly start another user conduct RFC, I'm not sure which. But let's not keep wasting time on this pointless discussion. Which is to say: I'm out. —David Eppstein (talk) 23:27, 4 November 2010 (UTC)
- No. Just more Brews bloat. Just because he can derive or prove something doesn't mean that WP:V is satisfied. The article is already well bloated with sourced stuff; why would we now start adding made up extra stuff? And why would he be pushing so hard this way, just back from a block, repeating the behavior that earned him a topic ban in physics? Simple, because the problem had nothing to do with physics, and everything to do with this kind of anti-collaborative editing behavior. Dicklyon (talk) 06:23, 5 November 2010 (UTC)
Just for the record: I don't think there is really an issue with WP:V or WP:NOR. I just think that there's no reason to bring up rotations in that context (because everything that is done there is independent of orientation) and because the section on proofs is already too long. — Carl (CBM · talk) 11:45, 5 November 2010 (UTC)
- Brews, That's a very interesting proof. I had never seen it before. I don't know why it is meeting with such resistance, but my advice to you is that if these guys here don't want it in the article, then you best drop the issue. As a side note, I have always believed that rotation is central to Pythagoras's theorem. David Tombe (talk) 14:57, 5 November 2010 (UTC)
- Carl: Thanks for your conclusion that no violations of WP:V and WP:SYN are present. Without the novelty introduced by introduction of the idea of Euclidean congruence transformations, I also agree with your earlier observation that the entire example including the part already in the main article is a meaningless addition and should be removed in its entirety, as I suggested myself days ago. The entire matter can be dropped, unless someone new shows up that seems to think rotational invariance is worth a mention. Brews ohare (talk) 16:19, 5 November 2010 (UTC)
Proof by subtraction
Isn't it necessary to show that the quadilateral in the center of the top panel is in fact a square? TomS TDotO (talk) 18:54, 7 November 2010 (UTC)
- In a full proof, yes. But this article just gives a sketch. Here are the key points:
- All four sides are the same length, because they are all the same length as the hypotenuse of the triangle. Remember all four triangles are congruent.
- Each angle of the square is a right angle because there is a straight line (the bottom one is the easiest to see) made up of angle a, an angle of the square, and angle b. Since a and b add up to 90 degees, and a straight line is 180 degrees, the angle of the square is indeed 90 degrees.
- — Carl (CBM · talk) 19:03, 7 November 2010 (UTC)

- Just looking at it and this one is also a duplicate, of the first rearrangement proof: it's just turned on its side and drawn as two squares instead of an animated GIF, with the first and last frames of the animation the same as the upper and lower squares. As with Garfield's proof there seems no point having proofs that just repeat another already given, especially as, as other editors have noted, the proof section is too long. Any objection to removing these two as duplicates?--JohnBlackburnedeeds 20:55, 7 November 2010 (UTC)
- This proof, like all of them, is logically equivalent. The difference is the imagined subtraction of areas from a larger square, which is perhaps more visual than a more algebraic approach, and so may be more compelling for some readers. Brews ohare (talk) 23:57, 7 November 2010 (UTC)
- No, it's not the same as the algebraic proof, but the first rearrangement one above it. I've re-done the image, at right, to make it clearer (bigger mostly though I introduced more steps to the anim and run it only one way) and if you examine the first and last frames (the labelled ones where it pauses) they are the same as the images in the subtraction proof, just rotated 90° and differently coloured and labelled.--JohnBlackburnedeeds 00:25, 8 November 2010 (UTC)
- I think that the image there completely replaces the need for the "subtraction proof" in the article (which is good, IMHO, because I think there are too many proofs at the moment.) — Carl (CBM · talk) 03:04, 8 November 2010 (UTC)
- No, it's not the same as the algebraic proof, but the first rearrangement one above it. I've re-done the image, at right, to make it clearer (bigger mostly though I introduced more steps to the anim and run it only one way) and if you examine the first and last frames (the labelled ones where it pauses) they are the same as the images in the subtraction proof, just rotated 90° and differently coloured and labelled.--JohnBlackburnedeeds 00:25, 8 November 2010 (UTC)
- This proof, like all of them, is logically equivalent. The difference is the imagined subtraction of areas from a larger square, which is perhaps more visual than a more algebraic approach, and so may be more compelling for some readers. Brews ohare (talk) 23:57, 7 November 2010 (UTC)
Suit yourselves. I don't know who contributed this example initially. Brews ohare (talk) 03:48, 8 November 2010 (UTC)
Garfield's proof
This proof is just a more complex version of the first algebraic proof. I.e. if you take that square side a + b, bisect it along a diagonal of the inner square side c, you get a rhombus. The result is a much longer calculation, but apart from working out the area of the rhombus (1⁄2(a + b) of course) is the same as the calculation in the earlier proof, with a multiply by two also needed to undo the bisection earlier. So it's not especially novel or original, unless because of the novelty of a US president also being intelligent, but that seem a poor reason to include a proof which just restates a previous one in a far more lengthy and complicated way.--JohnBlackburnedeeds 19:38, 7 November 2010 (UTC)
- Garfield's proof is not included because it is radically different from others, but only as a historical curiosity. For exactly that reason it appears in a number of books on Pythagoras' theorem. It may be the only example of a mathematical proof offered by a famous politician, a group not noted for such interests. Brews ohare (talk) 23:55, 7 November 2010 (UTC)
- The point is it duplicates a previous proof, except in a more complex way as it starts with a rhombus with area half the square, etc.. If it's only a historical curiosity it perhaps deserves a mention in the history section, or at the start of the section when the number of proofs is given. 00:30, 8 November 2010 JohnBlackburne
- You have stated your point about being a more complicated version of other proofs, John, and I accept that, but do not find it sufficient reason to reduce this proof to a sentence in the history section.
- Inclusion of Garfield's proof in the history section doesn't fit in with the present objectives of that section, which is about very early history in other civilizations and the priority of Pythagoras. I'd say the numerous appearances of this proof in books suggest the interest of many in this proof exceeds your own, and most probably includes many readers of this article. They may well enjoy appraising just how Garfield approached the matter. Brews ohare (talk) 04:06, 8 November 2010 (UTC)
- In addition, this section on Garfield's proof is useful in tracking down the original sources documenting his work. Brews ohare (talk) 04:08, 8 November 2010 (UTC)
A second similarity proof
This proof is redundant, and is covered exactly in this subsection on generalization. See the discussion of the second figure in this section. Brews ohare (talk) 04:26, 8 November 2010 (UTC)
- So take it out. Dicklyon (talk) 04:47, 8 November 2010 (UTC)
Bloat
This recent reversion by John Blackburne provides the reason: Unnecessary bloat: nothing to do with Pythagoras's thm. The removed statement is:
- These proofs depend upon an assumption of Euclidean geometry not stated in Euclid's fundamental axioms that certain movements of figures do not change their geometrical properties such as the lengths of sides and interior angles, the so-called Euclidean motions, which include translations and rotations of figures.
A number of deleted sources are provided to establish the role of Euclidean motions in Euclidean geometry.
I object to this reversion on these grounds:
1. "Bloat" is not a reason generally accepted as a WP criterion for reversion.
2. "Bloat" is very subjective appraisal, and editors may differ upon what is or isn't bloat. In this case I don't think it is bloat, but an accurate and useful observation, with a connection to an important topic. It is only one sentence anyway.
3. The underpinnings of Euclidean geometry are not specifically related to Pythagoras theorem, but almost all the proofs of the theorem depend upon translating, rotating, or reflecting figures, which are exactly the motions assumed to leave geometric properties invariant. Any reader looking at these proofs might find it of interest to pursue this topic using the references deleted.
4. The material is pertinent and very well sourced, and so satisfies all WP criteria for inclusion. Brews ohare (talk) 17:55, 8 November 2010 (UTC)
- WP is decided by consensus, and three editors have now reverted your additions of this material so the consensus on this is clear. But for the record my own reasons were the addition is nothing to do with Pythagoras's theorem. These proofs depend on many things, far more than your addition indicates. But it says in the very first sentence that this is a theorem in Euclidian geometry. There's no need to highlight which particular bits some of the proofs depend on, the same as there's no need to highlight that the algebraic proofs depend on completing the square, or the calculus proof depends on rather more.--JohnBlackburnedeeds 18:38, 8 November 2010 (UTC)
- Basically, I agree. The insufficient rigor of Euclid's axioms relative to more carefully chosen axiom sets such as Hilbert's is an important topic in elementary geometry, but it's a separate topic, not part of the subject of the Pythagorean theorem. —David Eppstein (talk) 18:56, 8 November 2010 (UTC)
- I'd agree that the rigor of Euclid's axioms is not properly discussed here, but that is not the purpose of this sentence. It's purpose is to point out the use of translations and rotations in the proofs of Pythagoras' theorem is not an unexamined topic, and can be pursued by the interested reader by consulting the provided sources. IMO anyone would notice the use of these transformations in the proofs, and some might query their status. It is hardly a disservice to the reader to provide these hooks for further exploration.
- Basically, I agree. The insufficient rigor of Euclid's axioms relative to more carefully chosen axiom sets such as Hilbert's is an important topic in elementary geometry, but it's a separate topic, not part of the subject of the Pythagorean theorem. —David Eppstein (talk) 18:56, 8 November 2010 (UTC)
- Apparently we disagree upon one role of a WP article as being the expansion of reader awareness of the ramifications of a topic. Personally, I find this aspect to be one of the cardinal virtues of a WP article. Brews ohare (talk) 19:09, 8 November 2010 (UTC)
- For reference, here's the removed material:
These proofs depend upon an assumption of Euclidean geometry not stated in Euclid's fundamental axioms that certain movements of figures do not change their geometrical properties such as the lengths of sides and interior angles, the so-called Euclidean motions, which include translations and rotations of figures.
-
- The angle of rotation of the square in the top panel of this example is the same as the smaller acute angle of the four right triangles.
-
- The general topic is that of Euclidean motions; see, for example: Luciano da Fontoura Costa, Roberto Marcondes Cesar (2001). Shape analysis and classification: theory and practice. CRC Press. p. 314. ISBN 0849334934. and Helmut Pottmann, Johannes Wallner (2010). Computational Line Geometry. Springer. p. 60. ISBN 3642040179.
- Richard J. Trudeau (2008). "Euclid's axioms". The Non-Euclidean Revolution. Birkhäuser. pp. 39 'ff. ISBN 0817647821.
- See, for example: Luciano da Fontoura Costa, Roberto Marcondes Cesar (2001). Shape analysis and classification: theory and practice. CRC Press. p. 314. ISBN 0849334934. and Helmut Pottmann, Johannes Wallner (2010). Computational Line Geometry. Springer. p. 60. ISBN 3642040179. The group of motions underlie the metric notions of geometry. See Félix Klein (2004). Elementary Mathematics from an Advanced Standpoint: Geometry (Reprint of 1939 Macmillan Company ed.). Courier Dover. p. 167. ISBN 0486434818.
- I've checked the refs, but don't find support for Dr. Brews's assertion that "These proofs depend upon an assumption of Euclidean geometry not stated in Euclid's fundamental axioms." They appear rather to affirm that congruence comes directly out of Euclid. I'd need to see a source to think other than that this is yet another Brews idiosyncratic interpretation. Of course, I may have just missed it, in which case he can simply point it out, and then say what indicates that it should be discussed in the context of the Pythagorean theorem. Dicklyon (talk) 06:39, 9 November 2010 (UTC)

 , there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.
, there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.  where f is dimensionless. Ignoring the question of whether dimensional analysis is a valid proof technique at all (which I would say it is not), the assumption about the form of the area is far from obvious. It would be equally possible for the area to be of the form
where f is dimensionless. Ignoring the question of whether dimensional analysis is a valid proof technique at all (which I would say it is not), the assumption about the form of the area is far from obvious. It would be equally possible for the area to be of the form  where g has units of length (for example, if g includes some constant that has units of length). It would even be possible, in principle, for the area to be of the form
where g has units of length (for example, if g includes some constant that has units of length). It would even be possible, in principle, for the area to be of the form  where h has units of (length). The deeper issue is that dimensional analysis is not a valid proof technique, but even if it was there is no reason that the area would need to be in the form specified in that argument. In general all that can be said is that the area can be written as some function of c, α, and β – the form of the function cannot be known ahead of time. — Carl (
where h has units of (length). The deeper issue is that dimensional analysis is not a valid proof technique, but even if it was there is no reason that the area would need to be in the form specified in that argument. In general all that can be said is that the area can be written as some function of c, α, and β – the form of the function cannot be known ahead of time. — Carl (